Hi everyone,
It appears that there is no issue with the analytical solution here, right? (I might have overhead something, because I could not read all posts, as I am on a mobile phone.)
sol = DSolveValue[{y''[x] - (s + x)*y[x] == 0, y'[0] == -1, y[M] == 0}, y[x], x]
(*(-AiryAi[s + x] AiryBi[M + s] + AiryAi[M + s] AiryBi[s + x])/(AiryAiPrime[s] AiryBi[M + s] - AiryAi[M + s] AiryBiPrime[s])*)
Then we can calculate
limit=Limit[sol, M -> Infinity]
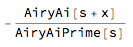
It seems to be ok-ish, from what I can see now:
D[limit, x, x] - (s + x)*limit == 0
evaluates to True.
D[limit, x] /. x -> 0
gives -1; and
Limit[limit, x -> Infinity]
gives 0. From that we can generate very high precision results, of course.
But as the OP says, in the case they are interested in there is no analytical solution. So in order to suggest anything it would be useful to get the actual problem.
By the way, the example:
sol=NDSolve[{u''[x]-(s+x)*u[x]==0,u'[0]+1==0,u[L]==0},u[x],{x,0,L},WorkingPrecision->50,PrecisionGoal->32];
fails to run on my MMA11.0.0 on OSX 10.11.6, but it does run on MMA 10.4.1. I also get an error message that the maximum number of steps is reached before obtaining the requested precision, but that can be changed by adding something like this:
post = NDSolveValue[{u''[x] - (s + x)*u[x] == 0, u'[0] + 1 == 0, u[L] == 0}, u[x], {x, 0, L}, WorkingPrecision -> 50, PrecisionGoal -> 32, MaxSteps -> 10^6]
which does finish after quite some while. No joy on MMA11. There are several reasons why I think that your way of checking the precision is not quite ideal, but this is what I get using your approach:
rerror = u0/u0acc - 1
gives
$7.1796\cdot 10^{-27}$. Not quite what you want though.
Finally, if you use
solpost =
NDSolveValue[{u''[x] - (s + x)*u[x] == 0, u'[0] + 1 == 0, u[L] == 0},u[x], {x, 0, L}, WorkingPrecision -> 56, PrecisionGoal -> 39,
MaxSteps -> 10^6, InterpolationOrder -> All, Method -> "StiffnessSwitching" ]
your test gives basically what you might expect
$3.335\cdot10^{-32}$. You can play a bit with the parameters to improve on this.
And this here
solpost =
NDSolveValue[{u''[x] - (s + x)*u[x] == 0, u'[0] + 1 == 0, u[L] == 0},u[x], {x, 0, L}, WorkingPrecision -> 60, PrecisionGoal -> 45,
MaxSteps -> 10^7, InterpolationOrder -> All, Method -> "StiffnessSwitching" ]
gives
$1.1*10^{-34}$ for your "rerror".
Cheers,
Marco