Dear Alan,
this is a very nice example of how to be more efficient. Beautiful.
When I red you post I wondered whether I can find an order in which you might want to go through this words, assuming that you want to minimise the (single) changes to the dials - and ended up doing what Sander suggests. So if we take the words that you calculate:
letters = "B F r m d t s w p l
E l o I a u y r w h
K s n t m r e l a o
L y p e t s m k g d ";
dials = (ToLowerCase /@ StringSplit[#]) & /@
StringSplit[letters, "\n"];
tup = Tuples[dials];
strings = StringJoin /@ tup;
words = Select[strings, DictionaryWordQ];
Take the first two words of that list:
words[[1 ;; 2]]
(*{"best", "bent"}*)
In this case we need to move the s one step forward to get to the n, because when we change the third letter the dial looks like this:
{"k", "s", "n", "t", "m", "r", "e", "l", "a", "o"}
So the n is one after the s, which means one turn of dial 3 will do the trick. We also have to consider that the dial is circular (I hope it is...). That means that the distance between k and o is only one. In oder to achieve this I will first convert the dials to number form, and then define a function to measure the distance. Each dial has 10 elements, so
rules = Rule @@@ Transpose @{#, Range[0, 9]} & /@ dials;
rules // TableForm

are the transformation rules for the four dials. We can now transform the words into numeral codes:
worddigits =
Transpose[(#[[1]] /. #[[2]]) & /@ (Transpose@{Transpose[Characters[words]], rules})];
Next we define the distance function like so:
dist[a_, b_] :=
Total[If[Abs[#[[1]] - #[[2]]] < 5, Abs[#[[1]] - #[[2]]], 10 - Abs[#[[1]] - #[[2]]]] & /@ Transpose[{a, b}]]
There are nicer ways of achieving this using modulo but this one is intuitive and will do. Using this function we can confirm that the distance between the first two words is:
dist[worddigits[[1]], worddigits[[2]]]
is one. We will now use FindShortestTour with this new distance function.
shortestcircle = FindShortestTour[worddigits, DistanceFunction -> dist];
One of the problems is that the tour is a circle, i.e. we go back to the first word. As we only need each word once we can delete the (not necessarily unique) step which needs most rotations.
longeststep =
Flatten[Position[#, Max[#]] & @(dist[worddigits[[#[[1]]]], worddigits[[#[[2]]]]] & /@ Partition[Drop[shortestcircle[[2]], -1], 2, 1])][[1]];
The length of that step is 4 in our example and it occurs at
{16, 271, 361, 364, 828, 830}
We choose the first position in our function above. The next function calculates the order we should use:
order = RotateLeft[Drop[shortestcircle[[2]], -1], longeststep];
We can now display the order in which we should do this:
Shallow[words[[order]]]
{"roes", "foes", "fort", "fore", "fire", "firs", "firm", "form", \
"fork", "folk", <<833>>}
The total number of rotations of the dials is:
Total[dist[worddigits[[#[[1]]]], worddigits[[#[[2]]]]] & /@ Partition[order, 2, 1]]
which gives 1140. We can compare that to the original order
Total[dist[#[[1]], #[[2]]] & /@ Partition[worddigits, 2, 1]]
which gives 2622, which means that we only have to do about 43% of the original work. Note that this calculation ignores the original position of the dials. If we have it, then we can just add it to the original list and at the end RotateLeft the order to that starting "word".
Note, that our order is actually quite good. If you look at the histogram of the number of steps/rotations from one word to the next you get:
BarChart[#[[All, 2]], ChartLabels -> #[[All, 1]], PlotTheme -> "Scientific",
LabelStyle -> Directive[Bold, Medium]] &@Tally[dist[worddigits[[#[[1]]]], worddigits[[#[[2]]]]] & /@ Partition[order, 2, 1]]
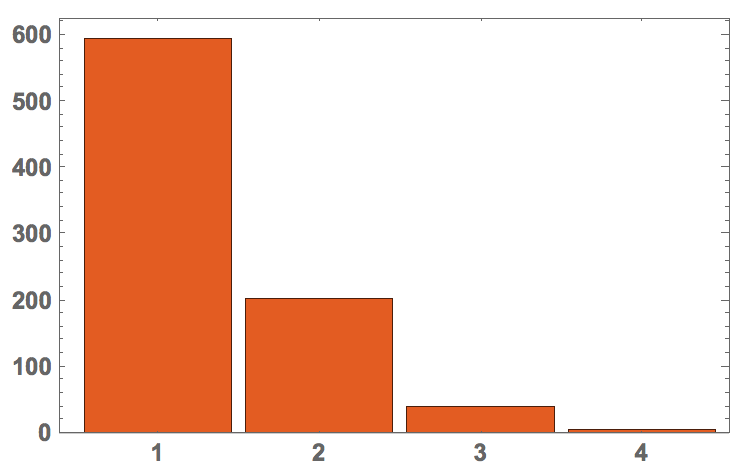
Hence, most of the times we only need one step. If we compare that to the original order
BarChart[#[[All, 2]], ChartLabels -> #[[All, 1]], PlotTheme -> "Scientific",
LabelStyle -> Directive[Bold, Medium]] &@SortBy[Tally[dist[#[[1]], #[[2]]] & /@ Partition[worddigits, 2, 1]], 2]
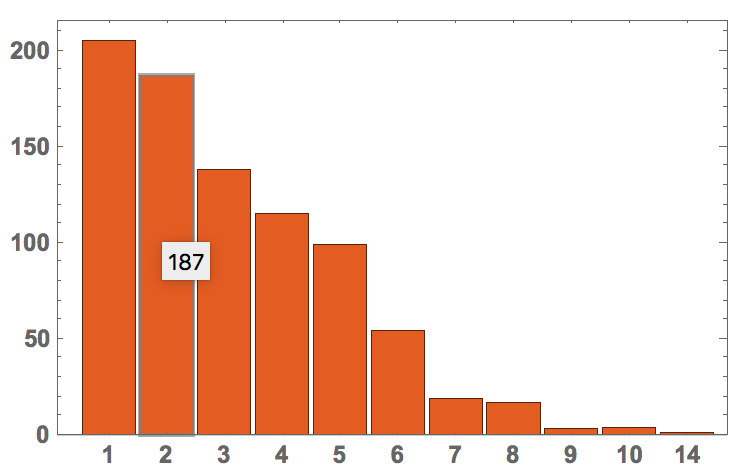
it becomes clear that we have somewhat improved. I hope that this helps all the rotation lock pickers out there...
Cheers,
Marco
PS: I was quite curious which words might need 14 (!) rotations of the dials. They are words 328 and 329: "mule" and "desk". On the dials given they in fact need 14 rotations.
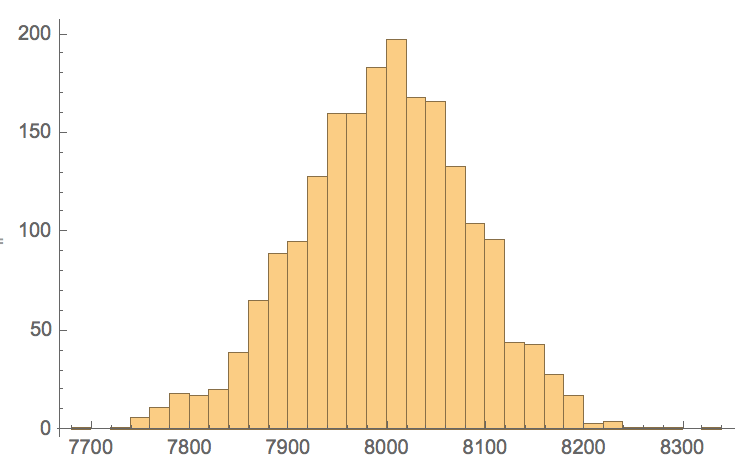
Obviously an alphabetical order is worse than our order, but still much better than a random order of words:
numberofswitches =
Table[Total[dist[#[[1]], #[[2]]] & /@ Partition[RandomSample[worddigits], 2, 1]], {2000}];
Histogram[numberofswitches]