Group Abstract Group Abstract

Message Boards Message Boards

0
|
6.2K Views
|
3 Replies
|
3 Total Likes
View groups...
Share
Share this post:

Finding aspects of a plot of route in the tour de france for a project?

Peter Feenstra
Posted 9 years ago
POSTED BY: Peter Feenstra
3 Replies
Sort By:

The code that I wrote should (in pricinple) just work in 3D since EuclideanDistance and Norm work with any dimensions. Just re-write fn
POSTED BY: Jon McLoone
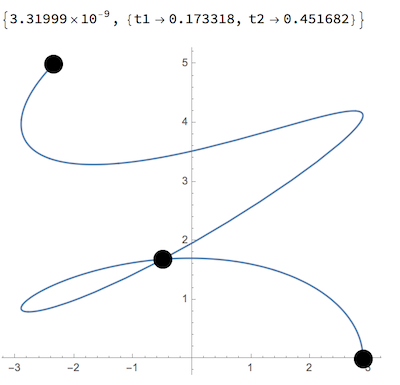
  1. Can be done as...
    fn[t_] := {2.9 Cos[3.2 Pi t], Sin[4 Pi t] + 5 t};

    ans = NMinimize[{EuclideanDistance[fn[t1], fn[t2]],  0 < t1 < 1 && 0 < t2 < 1 && t1 < t2 - 0.1}, {t1, t2}]

    ParametricPlot[fn[t], {t, 0, 1},  Epilog -> 
        {PointSize[0.05], Point[fn[0]],    Point[fn[1]], {Point[fn[t1]], Point[fn[t2]]} /. ans[[2]]}]

enter image description here

And 3. can be done as

Plot[Evaluate[Norm[D[fn[t], t]]], {t, 0, 1}]

enter image description here
POSTED BY: Jon McLoone
Peter Feenstra
Peter Feenstra
Posted 9 years ago

Thank you for your help Jon. So i realized that the plot can be represented better in ParametricPlot3D when the z-direction is set to 0. ft_] = ParametricPlot3D[{2.9 Cos[3.2 [Pi],Sin4 [Pi] + 5 t, 0}, {t, 0, 1}]

Once this has been applied, it seems to not jive with your suggested material. Is there a way to apply what you did into the third dimension?
POSTED BY: Peter Feenstra
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard