Introduction
I recently saw a TV show set at Four Corners USA, the point where Utah, Colorado, Arizona, and New Mexico meet:
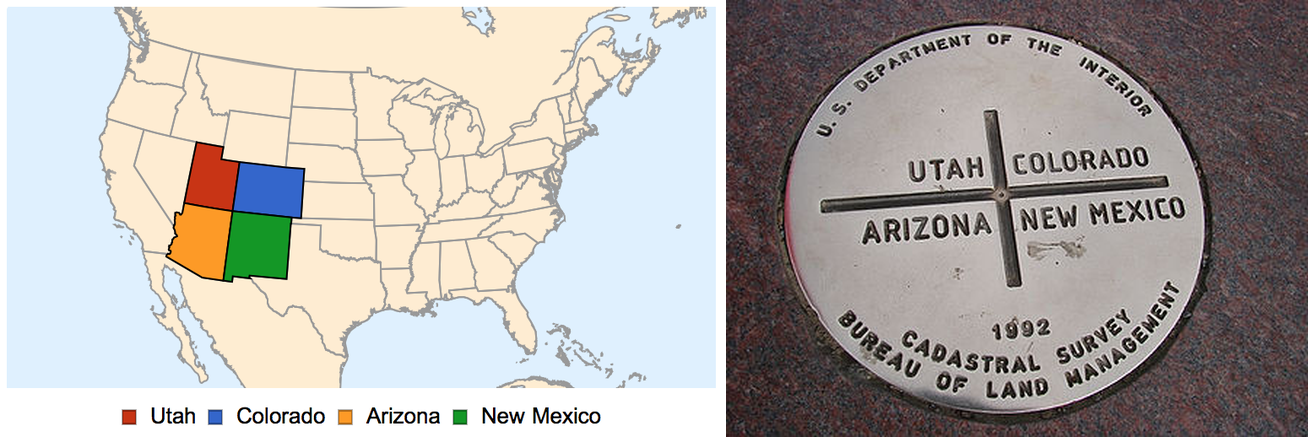
It made me wonder how frequent 4 or more geographical borders meet at one point. According to Wikipedia, 4 borders meeting at a point is called a quadripoint, 5 borders meeting is called a quintipoint, and in general it's called a multipoint. The entry only lists one quintipoint and goes on to say
Perhaps a dozen quintipoints of various levels of geopolitical subdivisions are scattered around the world;
This piqued my interest to find all multipoints, using the Wolfram Language.
Results
Before I give the details on how to detect multipoints, I'd like to showcase the results.
Summary
- Since borders are not always precise (or even well defined at times), I allowed for an error up to ~100 meters when classifying points.
- The polygons were obtained from the
"Country" and "AdministrativeDivision" Entity types (about 40,000 in total).
- There are a total of 724 quadripoints in this dataset.
- There are a total of 13 quintipoints in this dataset.
- There is 1 10-point in this dataset!
- There are only 6 multipoints in the dataset whose regions don't share the same parent region.
Quadripoints
With 724 quadripoints, there are too many to list here, but here are a few interesting ones.
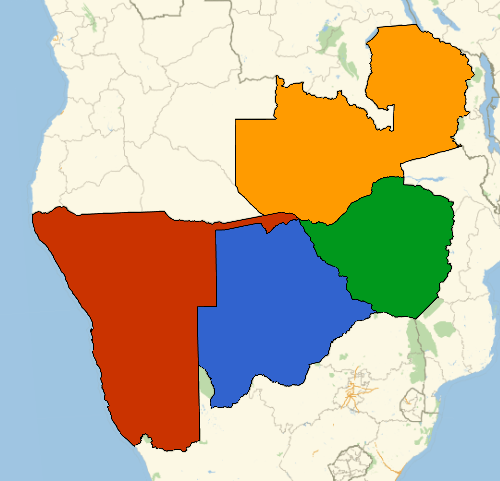
- The only countries to form a quadripoint are Namibia, Botswana, Zambia, and Zimbabwe.
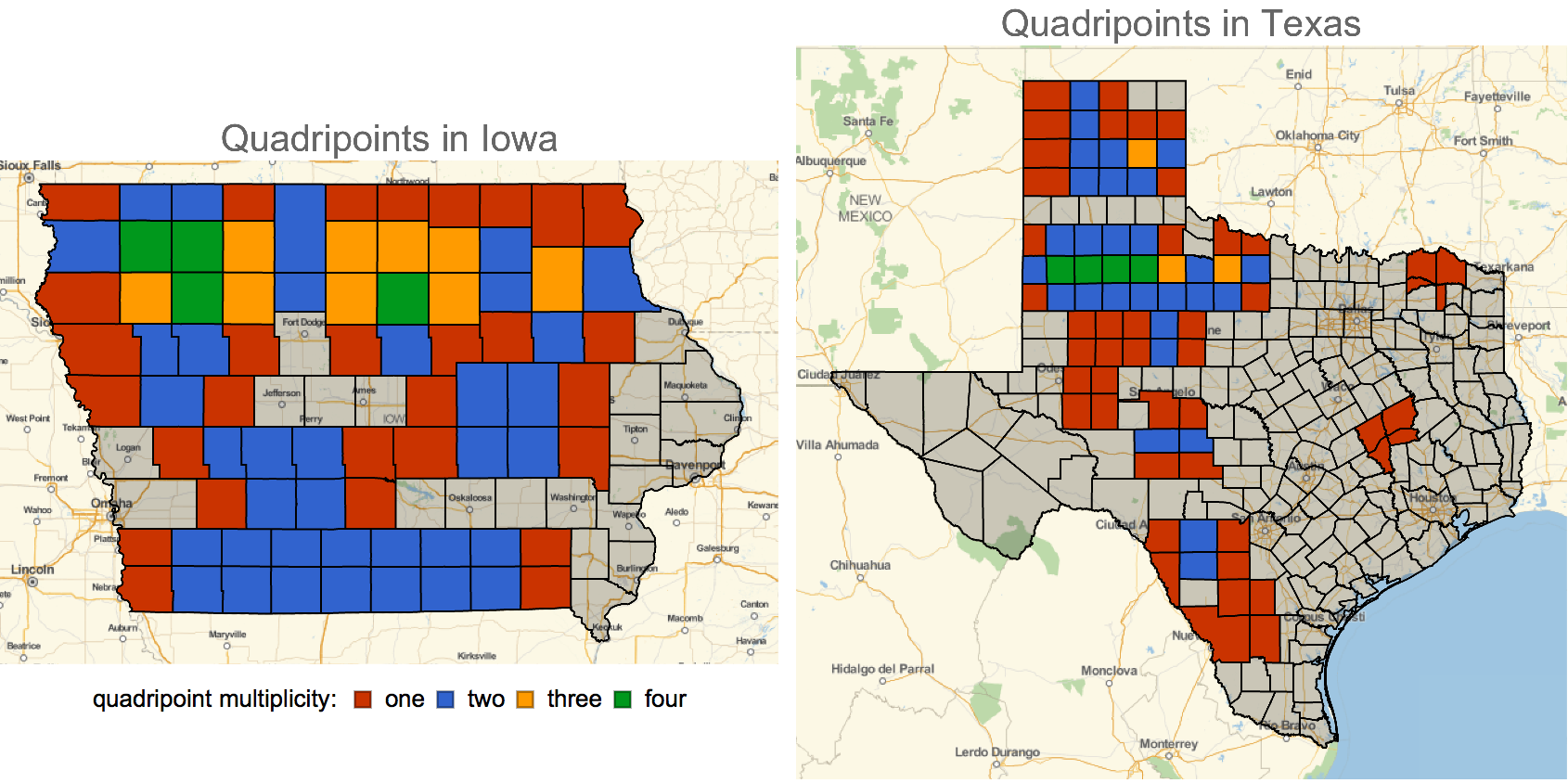
- There are a considerable amount of counties in Iowa and Texas that are apart of multiple quadripoints, i.e. more than one corner is a quadripoint. This is because they are roughly arranged in a rectangular grid.
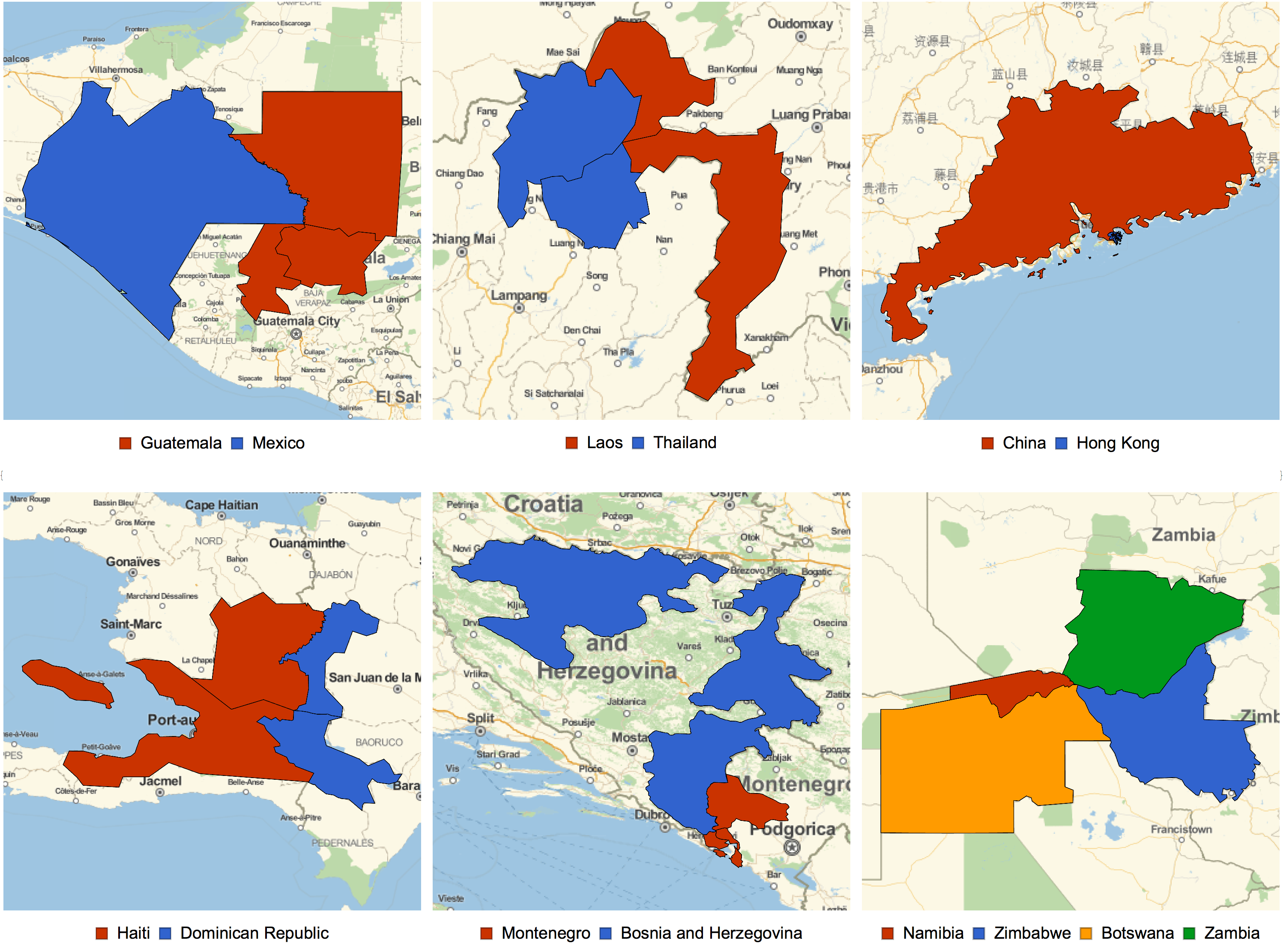
- There were only 6 quadripoints found whose parent regions differ:
- Here's a visual summary of all quadripoints found (note the level 3 regions were heavily thickened to become visible):
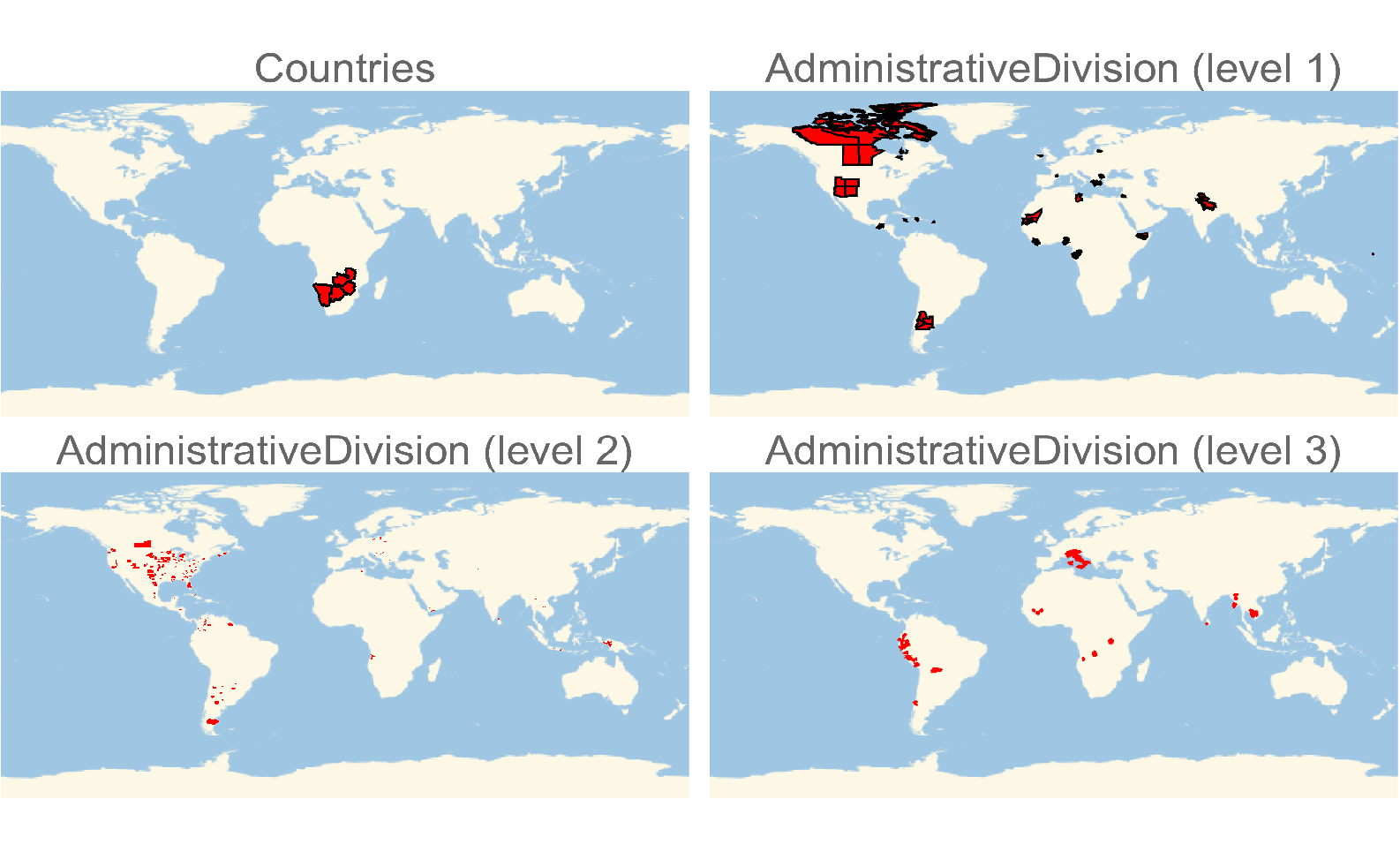
Quintipoints
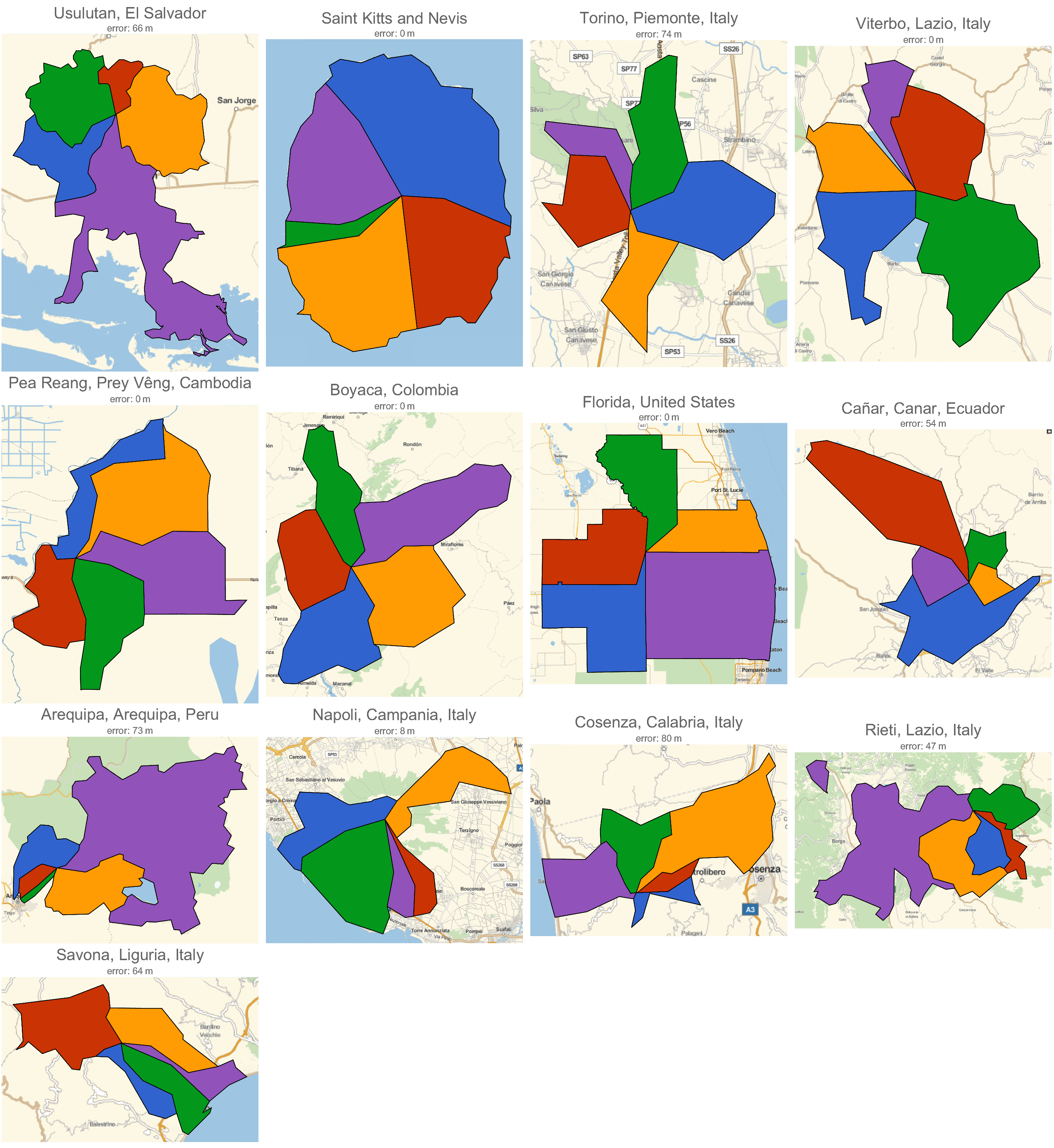
Here are all 13 quintipoints found:
- Saint Kitts and Nevis: Saint George Gingerland - Saint James Windward - Saint John Figtree - Saint Paul Charlestown - Saint Thomas Lowland
- Boyaca, Colombia: Chinavita - Garagoa - Miraflores - Ramiriquí - Zetaquirá
- Counties in Florida, USA: Glades - Hendry - Martin - Okeechobee - Palm Beach
- Usulutan, El Salvador: California - Ozatlán - Santa Elena - Tecapán - Usulután
- Arequipa, Arequipa, Peru: Alto Selva Alegre - Cayma - Chiguata - Miraflores - San Juan de Tarucani
- Cuenca, Azuay, Ecuador: Chiquintad - Cuenca - Ricaurte - Sidcay - Sinicay
- Pea Reang, Prey Vêng, Cambodia: Kampong Popil - Mesa Prachan - Prey Sralet - Reab - Roka
- Rieti, Lazio, Italy: Borgo Velino - Castel Sant' Angelo - Cittaducale - Micigliano - Rieti
- Cosenza, Calabria, Italy: Marano Marchesato - Marano Principato - Rende - San Fili - San Lucido
- Napoli, Campania, Italy: Boscotrecase - Ercolano - Ottaviano - Torre Del Greco - Trecase
- Savona, Liguria, Italy: Bardineto - Boissano - Giustenice - Loano - Pietra Ligure
- Torino, Piemonte, Italy: Cuceglio - Mercenasco - Montalenghe - Scarmagno - Vialfrè
- Viterbo, Lazio, Italy: Bolsena - Capodimonte - Gradoli - Montefiascone - San Lorenzo Nuovo
As you can see, Italy takes the cake with 6 quintipoints! Here's a visual of these quintipoints, along with the error allowing them to be classified as such:
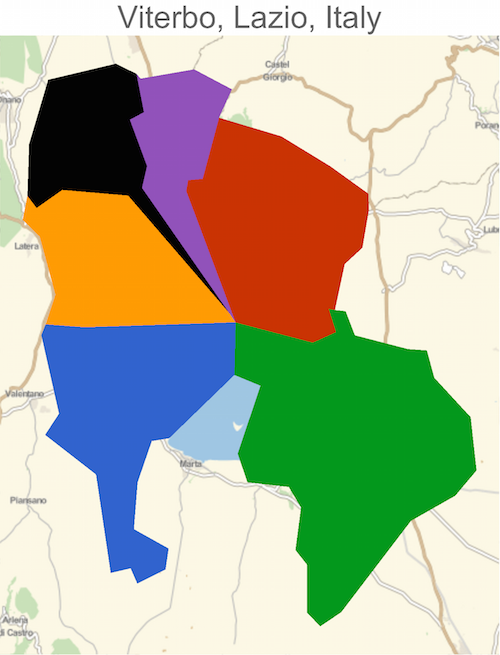
A Near 6-point
Notice in the top right map above, it looks like there is room for one more region in Viterbo, Lazio, Italy, which would make it a 6-point. Here's the 6th region (Grotte Di Castro) in black:
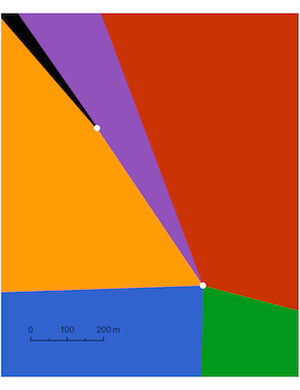
It turns out Grotte Di Castro is about 700 meters from the quintipoint, making this only a near 6-point:
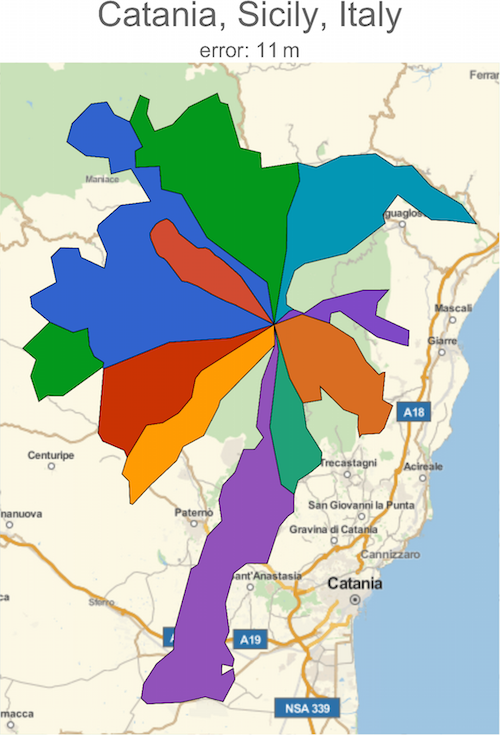
10-point
As mentioned in the Wikipedia entry, there is a 10-point in Italy at the summit of Mount Etna:
- Catania, Sicily, Italy: Adrano - Belpasso - Biancavilla - Bronte - Castiglione Di Sicilia - Maletto - Nicolosi - Randazzo - Sant' Alfio - Zafferana Etnea
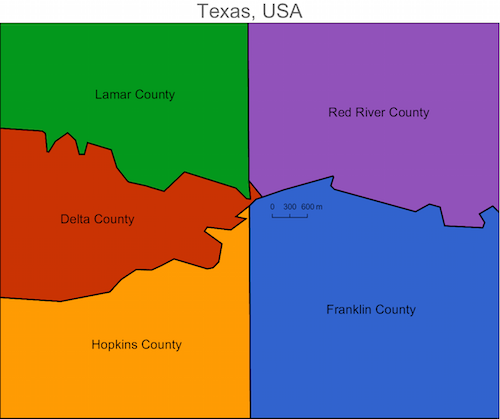
Allowing for more error
If we allow for more error, we can find near-multipoints - regions that almost have a multipoint, but clearly don't. For example, there is a near-quintipoint in Texas, USA:
Code
The idea to find multipoints within a collection of regions is as follows:
- Obtain the
Polygon for each region.
- For each pair of regions, if there's a vertex from one of the polygons which is "close" to the other, mark these regions as touching.
RegionDistance can be used for this.
- The relation of touching between pairs forms an adjacency matrix. From this, form a
Graph and use FindClique to find all multipoints in this collection.
Here is code that does just that:
discretize[Polygon[pts_?MatrixQ]] :=
MeshRegion[pts, Polygon[Range[Length[pts]]]]
discretize[Polygon[pts_?(VectorQ[#, MatrixQ] &)]] :=
With[{pts2 = Select[pts, Length[#] > 2 &]},
MeshRegion[Join @@ pts2,
Polygon[Range[# + 1, #2] & @@@ Partition[Prepend[Accumulate[Map[Length, pts2]], 0], 2, 1]]]
]
discretize[expr_] :=
With[{mr = DiscretizeGraphics[Graphics[expr]]},
mr /; MeshRegionQ[mr]
]
discretize[_] = $Failed;
polyLookup = discretize /@ (Join[
EntityValue["Country", "Polygon", "EntityAssociation"],
EntityValue["AdministrativeDivision", "Polygon", "EntityAssociation"]
] /. GeoPosition -> Identity);
MultiPoints[divs_List, n_] /; Length[divs] < n = {};
MultiPoints[divs_List, n_] :=
Block[{polys, disj, cands},
polys = polyLookup /@ divs;
(
disj = Boole[Outer[CoordinateNear, polys, polys]] - IdentityMatrix[Length[divs]];
(
cands = FindClique[AdjacencyGraph[divs, disj], {n, Infinity}, All];
resolveMultiPoints[cands, AssociationThread[divs, polys]]
) /; MatrixQ[disj, IntegerQ]
) /; VectorQ[polys, MeshRegionQ]
]
MultiPoints[___] = {};
$tol = 0.001;
CoordinateNear[mr1_, mr2_, tol_:$tol] :=
With[{d = {{-tol, tol}, {-tol, tol}}},
And[
NoneTrue[Transpose[{d+RegionBounds[mr1], d+RegionBounds[mr2]}], #1[[2,1]] > #1[[1,2]] || #1[[1,1]] > #1[[2,2]]&],
Min[RegionDistance[mr1, MeshCoordinates[mr2]]] < tol
]
]
resolveMultiPoints[{}, _] = {};
resolveMultiPoints[cands_List, passoc_?AssociationQ] :=
Select[cands, MultiPointQ[#, passoc]&]
MultiPointQ[cands_, passoc_?AssociationQ, tol_:$tol] :=
Block[{coords, mrs},
mrs = passoc /@ cands;
coords = Union @@ MeshCoordinates /@ mrs;
Or @@ Thread[And @@ (Thread[RegionDistance[#, coords] < tol]& /@ mrs)]
]
Now here's all multipoints formed from countries:

Now to explore all cases, we can start off by looking for multipoints in all subdivisions of a given region, e.g. given Florida, find all multipoints within the counties of Florida. This can be achieved by building a hierarchical graph connecting countries and administrative divisions. Then for a given region, this graph can be used to find all subdivisions and the above code can be used to find the multipoints.
ad = AdministrativeDivisionData[];
pr = EntityValue["AdministrativeDivision", "ParentRegion"];
$ADNetwork = Graph[Join[
Thread["NullPointer" -> EntityList["Country"]],
DeleteCases[Thread[pr -> ad], Rule[_Missing, _]]
]];
ChildrenMultiPoints[reg_] := ChildrenMultiPoints[reg, 4]
ChildrenMultiPoints[reg_, o___] :=
MultiPoints[Rest[VertexOutComponent[$ADNetwork, reg, 1]], o]

Lastly, to cover all cases we need to consider sets of regions that have differing parent regions. To do this, for a given parent region $P$, first find all other regions $R_i$ (on the same level) that touch this region. Then simply run MultiPoints on all subdivisions in $P \cup R_i$. I omit this code here, as there were only 6 instances that came out of this case.