I ran a few tests in an attempt to isolate the issue, but I'm still stuck without a solution. In each of these cases, I started with a freshly restarted kernel and the following initializtion code:
initialVelocity[pt_] := Module[
{y, v0, \[Theta]},
y = Norm[pt[[1 ;; 3]]]/(2 rd);
v0 = 4*\[Pi]*\[CapitalSigma]0*rd*
y^2 (BesselI[0, y]*BesselK[0, y] - BesselI[1, y]*BesselK[1, y]);
\[Theta] = ArcTan[pt[[1]], pt[[2]]];
{-v0 Sin[\[Theta]], v0 Cos[\[Theta]], 0.0, 0.0} +
RandomVariate[NormalDistribution[0, .0001], 4]
]
Needs["OpenCLLink`"];
source = {"D:\\Google Drive\\Mathematica\\nbody.cl"};
stepSimulation = OpenCLFunctionLoad[
source,
"nbody_kern",
{
"Float",
"Float",
{"Float", _, "Input"},
{"Float", _, "Input"},
{"Float", _, "Input"},
{"Float", _, "Output"},
{"Float", _, "Output"},
{"Float", _, "Output"},
{"Local", "Float"}
},
256, "ShellOutputFunction" -> Print
];
dt = .01;
eps = .0001;
rd = 1.0;
\[CapitalSigma]0 = 0.3;
len = 2^13;
particles = (RandomVariate[ExponentialDistribution[rd]]*{Cos[#],
Sin[#], 0.0, 0.0}) & /@ RandomReal[{0, 2 Pi}, len];
particles[[All, 4]] = 1.0/len;
velocity = initialVelocity /@ particles;
acceleration = Array[{0.0, 0.0, 0.0, 0.0} &, len];
position1 = OpenCLMemoryLoad[particles, "Float"];
velocity1 = OpenCLMemoryLoad[velocity, "Float"];
acceleration1 = OpenCLMemoryLoad[acceleration, "Float"];
position2 = OpenCLMemoryAllocate["Float", {len, 4}];
velocity2 = OpenCLMemoryAllocate["Float", {len, 4}];
acceleration2 = OpenCLMemoryAllocate["Float", {len, 4}];
The nbody.cl code is the same from the original post. After each test, I used the respective command below to keep track of my data between kernel resets.
DumpSave["memList1.mx", memList1];
DumpSave["memList2.mx", memList2];
DumpSave["memList3.mx", memList3];
DumpSave["memList4.mx", memList4];
Here are the details of each test I ran. Test 1 replicates my original conditions. Test 2 uses Arnoud's example for comparison. Test 3 keeps everything regarding the simulation on the GPU, and the Mathematica kernel only handles the loop and the memory tracking. Lastly, test 4 is the same as 3, except the kernel accesses the GPU memory to get the current particle positions at each step.
Test 1 pr = 8;
mem0 = MemoryInUse[];
memList1 = {MemoryInUse[] - mem0};
Graphics3D[{PointSize[Small],
Point[Dynamic[Refresh[AppendTo[memList1, MemoryInUse[] - mem0];
stepSimulation[dt, eps, position1, velocity1, acceleration1,
position2, velocity2, acceleration2, 256*4, len];
stepSimulation[dt, eps, position2, velocity2, acceleration2,
position1, velocity1, acceleration1, 256*4, len];
OpenCLMemoryGet[position1][[All, 1 ;; 3]],
UpdateInterval -> 0]]]},
PlotRange -> {{-pr, pr}, {-pr, pr}, {-pr/4, pr/4}}, ImageSize -> 1000]
Dynamic[ListLinePlot[memList1]]
Test 2mem0 = MemoryInUse[];
memList2 = {MemoryInUse[] - mem0};
Graphics3D[{PointSize[Small],
Point[Dynamic[Refresh[AppendTo[memList2, MemoryInUse[]];
RandomReal[1, {len, 3}], UpdateInterval -> 0]]]},
PlotRange -> {{0, 1}, {0, 1}, {0, 1}}, ImageSize -> 1000]
Dynamic[ListLinePlot[memList2]]
Test 3 mem0 = MemoryInUse[];
memList3 = {MemoryInUse[] - mem0};
Do[
AppendTo[memList3, MemoryInUse[] - mem0];
stepSimulation[dt, eps, position1, velocity1, acceleration1,
position2, velocity2, acceleration2, 256*4, len];
stepSimulation[dt, eps, position2, velocity2, acceleration2,
position1, velocity1, acceleration1, 256*4, len];
, {15000}]
Test 4 mem0 = MemoryInUse[];
memList4 = {MemoryInUse[] - mem0};
Do[
AppendTo[memList4, MemoryInUse[] - mem0];
stepSimulation[dt, eps, position1, velocity1, acceleration1,
position2, velocity2, acceleration2, 256*4, len];
stepSimulation[dt, eps, position2, velocity2, acceleration2,
position1, velocity1, acceleration1, 256*4, len];
OpenCLMemoryGet[position1][[All, 1 ;; 3]];
, {15000}]
Results
After all of these had run, I used
Get /@ {"memList1.mx", "memList2.mx", "memList3.mx", "memList4.mx"};
to recover the memory tracking data. The results are interesting:
ListLinePlot[{memList1, memList2, memList3, memList4},
PlotStyle -> Thick,
PlotLegends -> Automatic,
PlotRange -> {{1, 15000}, Automatic},
AxesOrigin -> {1, -10^9}]
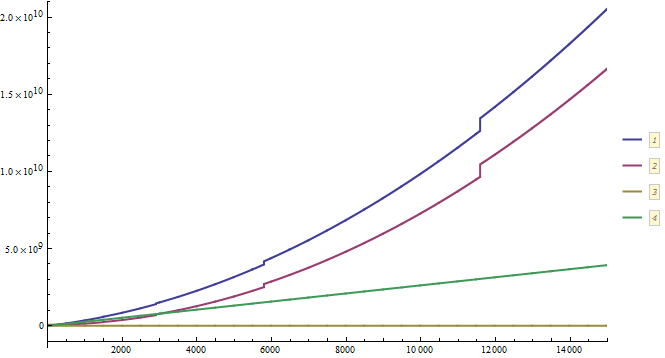
The memory usage from tests 1 and 2 is clearly a problem, since it appears to be increasing quadratically with each step. I ended up using an additional 20 GB of memory after 15000 steps. Although there's clearly a memory leak here somewhere that isn't OpenCL related, there's still a difference between test 1 and 2 that must be related to the OpenCL code. Although it's not as severe, it's the one I can't avoid, so I need to pin that one down.
The results from test 3 show that the simulation running on the GPU alone isn't the problem. I verified that the code did in fact run by getting the final position state afterwards, and everything appeared to have functioned properly. However, this code is entirely useless to me, since I need the particle positions at each step. Unfortunately, as you can see from the test 4 results, reading the position data from the GPU (even though I'm not assigning it to anything) increases the amount of memory in use linearly with every step. After 15000 steps, I was using approximately 4 GB of additional memory.
So from what I can tell is that using the function OpenCLMemoryGet[] is copying GPU memory to the kernel, but it never lets it go. This becomes a serious problem when you need to repeatedly get updates from the GPU, since each time the memory is read, a new section of kernel memory is allocated for it. What I need is some way to free up this memory from the kernel, but I have no idea how to refer to it. The function OpenCLMemoryUnload[] seems like it would be the obvious choice, but that is for unloading the memory I have allocated in the GPU, which doesn't help me. Does anyone know of a way to clear this memory from the kernel after each step?