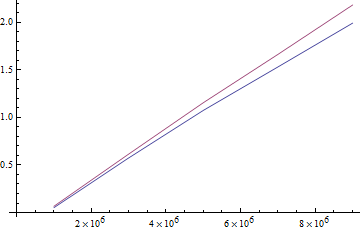
It looks like these two methods actually take the same amount of time (on average) to compute.
In[1]:= p = Table[Prime[n], {n, #}] &;
In[2]:= a = Table[
{n, First[Timing[Prime[Range[PrimePi[n]]]]]},
{n, 1000000, 10000000, 500000}];
In[3]:= b = Table[
{n, First[Timing[p[PrimePi[n]]]]},
{n, 1000000, 10000000, 500000}];
In[4]:= ListLinePlot[{a, b}]

EDIT: After a bit more testing, it does seem like Prime[Range[PrimePi]] is slightly faster, but they seem close enough so that the decision could be made based on personal preference.
am = Mean[Table[
{n, First[Timing[Prime[Range[PrimePi[n]]]]]},
{50},
{n, 1000000, 10000000, 2000000}]
];
bm = Mean[Table[
{n, First[Timing[p[PrimePi[n]]]]},
{50},
{n, 1000000, 10000000, 2000000}]
];
ListLinePlot[{am, bm}]