Message Boards Message Boards

0
|
8550 Views
|
6 Replies
|
3 Total Likes
View groups...
Share
Share this post:
GROUPS:
Optimization

First n primes

Hi,
Is there a "best practices" way to generate the first n primes? Two ways immediately spring to mind:
Select[Range[n],PrimeQ]
Prime[Range[PrimePi[n]]]
According to my internal picture of "what good Mathematica looks like", the last one is a whole lot more likely to be faster. However, in real life, it's not. The first option is considerably quicker, although it does use a bit more memory.
Given the ease of sieving for primes, I'd have thought there would be a better way to do this. Is there a correct way to specify the problem so that Mathematica knows to just return the output of a sieve, rather than having to deal with each prime in turn?

EDITED the first example was erroneously written as Select[Range[PrimePi@n], PrimeQ]
POSTED BY: Patrick Stevens
6 Replies
Sort By:
Paul Cleary
Paul Cleary
Posted 12 years ago
I just use
Prime[Range[n]]
to generate n primes, here are some timeings as comparison.
k = Prime[Range[1000000]]; // AbsoluteTiming
{1.6536029, Null}
l = Prime[Range[PrimePi[15485863]]]; // AbsoluteTiming
{1.653603, Null}

Paul.
POSTED BY: Paul Cleary
Just FYI: Using NextPrime iteratively is really bad choice. I just tried, 6-7 times slower than either of the other two methods.
POSTED BY: Sander Huisman
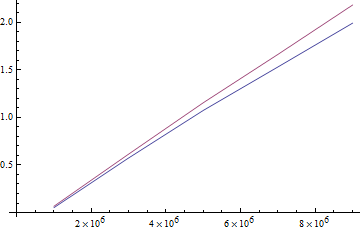
It looks like these two methods actually take the same amount of time (on average) to compute.
 In[1]:= p = Table[Prime[n], {n, #}] &;
 
 In[2]:= a = Table[
 {n, First[Timing[Prime[Range[PrimePi[n]]]]]},
 {n, 1000000, 10000000, 500000}];
 
 In[3]:= b = Table[
 {n, First[Timing[p[PrimePi[n]]]]},
 {n, 1000000, 10000000, 500000}];

In[4]:= ListLinePlot[{a, b}]


EDIT: After a bit more testing, it does seem like Prime[Range[PrimePi]] is slightly faster, but they seem close enough so that the decision could be made based on personal preference.
 am = Mean[Table[
     {n, First[Timing[Prime[Range[PrimePi[n]]]]]},
     {50},
     {n, 1000000, 10000000, 2000000}]
    ];
 
 bm = Mean[Table[
     {n, First[Timing[p[PrimePi[n]]]]},
     {50},
    {n, 1000000, 10000000, 2000000}]
   ];

ListLinePlot[{am, bm}]
POSTED BY: Richard Hennigan
@Shenghui - thanks, I didn't mean to put the extra PrimePi into the first one (which you evaluated second).
@Steven - it's not as fast as Prime@Range@PrimePi is - presumably because Prime is Listable. The millionth prime is 15485863:
In[35]:= Prime[Range[PrimePi[15485863]]]; // AbsoluteTiming
Out[35]= {4.762213, Null}

In[38]:= p[1000000]; // AbsoluteTiming
Out[38]= {5.087068, Null}
These results are the same when the system cache is cleared in between.
POSTED BY: Patrick Stevens
p = Table[Prime[n],{n,#}] &;
p @ 10000

 basically copied from the Prime help page seems to be simple and fast.
POSTED BY: Steven Christensen
@Patrick, actually these two code does not produce same result. Please try n =10000
POSTED BY: Shenghui Yang
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract