Plant 11 trees to get 16 lines of 3 trees. (Friedman, Tree Planting Problems)
Plant 19 trees to get 20 lines of 4 trees. (Friedman, Tree Planting Problems)
Plant 25 trees to get 18 lines each having 5 trees. (Elkies, On some points-and-lines problems )
Plant 62 trees on the Earth to get 15 lines of 12 trees. (Answer)

The modern father of recreational math Martin Gardner would have turned 102 today, so I thought I'd take a look at the orchard-planting problem. I'm never content to just quote previous work, so I looked closely at that "25 trees to get 18 lines each having 5 trees" configuration. The points were at simple barycentric coordinates. What are those? Consider a triangle with vertices A, B, C and an area of 1. Add an interior point D. The barycentric coordinates of D are the areas of triangles ABD, ADC, and DBC. The sum of the coordinates equals one since the original triangle had area 1. I used barycentric coordinates in my previous discussion Zak's Triangle.

Here's a picture. A =(1,0,0), B =(0,1,0), C =(0,0,1). For the interior points, you'll need to add a step -- divide by the total. The point marked 210 is (2/3, 1/3, 0). The point marked 123 is (1/6, 1/3, 1/2). Showing them as fractions would be a much messier picture.

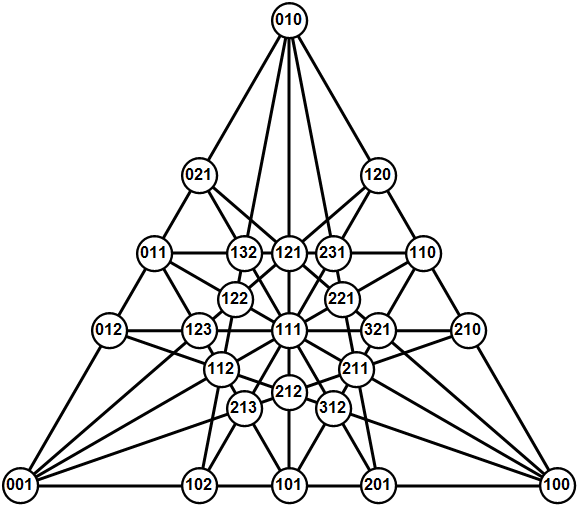
Code for that. First a triangle, then code for converting to and from barycentric coordinates.

tri = {{Sqrt[3], -1}, {0, 2}, {-Sqrt[3], -1}};

ToBarycentrics[{{x1_, y1_}, {x2_, y2_}, {x3_, y3_}}, {p_, q_}] := Solve[{m*x1 + n*x2 + (1 - m - n)*x3, m*y1 + n*y2 + (1 - m - n)*y3} == {p, q}];

FromBarycentrics[{m_, n_}, {{x1_, y1_}, {x2_, y2_}, {x3_, y3_}}] := {m*x1 + n*x2 + (1 - m - n)*x3, m*y1 + n*y2 + (1 - m - n)*y3};  

Next, it's handy to have barycentric lines. A barycentric point a b c is on a barycentric line A B C if their dot product A a + B b + C c equals 0. A canonical barycentric line can have three forms:

1. (a, b, c) with total 1.
2. (a, -1-a, 1) with total 0, going through the center point (1/3, 1/3, 1/3).
3. (1,-1,0), the vertical line through the center point.

Here's code for finding a barycentric line and finding the intersection point of two barycentric lines:

BaryLiner[{pt1_, pt2_}] := Module[{a, b},
  If[Det[{pt1, pt2, {1, 1, 1}/3}] != 0,
   {a, b, 1 - a - b} /. 
    Solve[{a, b, 1 - a - b}.# == 0 & /@ {pt1, pt2}][[1]],
   If[pt1[[1]] != pt1[[2]] ,
    {a, -1 - a, 1} /. 
     Solve[{a, -1 - a, 1}.# == 0 & /@ {pt1, pt2}][[1]],
    {1, -1, 0}
    ]]];

lineintersect[{{a1_, b1_, c1_}, {a2_, b2_, c2_}}] := 
  With[{init = {b1 c2 - b2 c1, a2 c1 - a1 c2, a1 b2 - a2 b1}}, 
   If[Total[init] == 0, init, init/Total[init]]];

With those pieces of code, I was able to find some more extreme orchards. Here's 72 trees making 57 rows of 6 or more trees. There are also 27 lines of 4 trees.

peggpoints = Sort[#/Total[#] & /@ Flatten[(Permutations /@ {{0, 0, 1}, {0, 1, 1}, {0, 1, 2}, {0, 4, 5}, {1, 1, 2}, {1, 2, 2}, {1, 2, 3}, {1, 2, 6}, {1, 4, 4}, {2, 2, 3}, {2, 2, 5}, {2, 3, 4}, {2, 3, 5}, {2, 5, 5}, {2, 6, 7}, {4, 5, 6}}), 1]];  
pegglines = First /@ Select[SortBy[Tally[BaryLiner[#] & /@ Subsets[peggpoints, {2}]], Last], Last[#] > 5 &];  
linecoords = Table[FromBarycentrics[{#[[1]], #[[2]]}, tri] & /@ Select[peggpoints, pegglines[[n]].# == 0 &], {n, 1, Length[pegglines]}];  
Graphics[{AbsoluteThickness[1], {{White, White, White, Cyan, Red, Black, Green, Magenta}[[Length[#]]], Line[#]} & /@ linecoords, 
  With[{coord = FromBarycentrics[{#[[1]], #[[2]]}, tri]}, {Black, Disk[coord, .057], White, Disk[coord, .054], Black, Style[Text[StringJoin[ToString /@ (# (Max[Denominator[#]]))], coord], 8]}] & /@ peggpoints}, ImageSize -> {600, 520}]

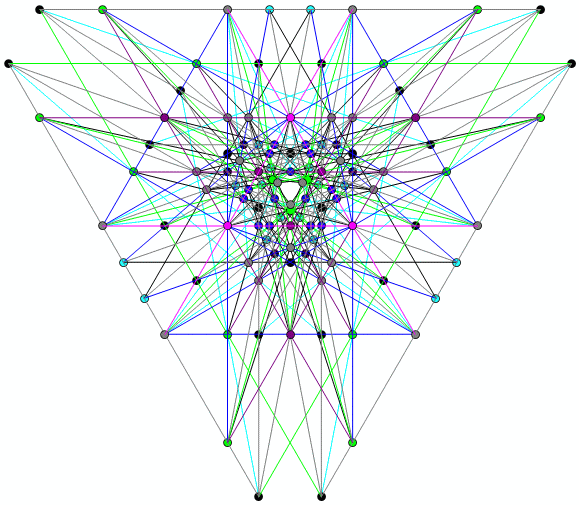
After finding that, I started thinking about something -- all the coordinates had sum one, and all the lines not through the center had sum one. Could I find a really nice configuration where the point set and the line set were the same? Here's one base set. See the notebook for full code.

base = {{-5, 3, 4}, {-4, 3, 5}, {-2, -1, 6}, {-2, 1, 2}, {-2, 1, 3}, {-1, 0, 2}, {-1, 0, 3}, {-1, 1, 1}, {-1, 1, 2}, {-1, 1, 3}, {-1, 2, 2}, {-1, 2, 3}, {-1, 3, 3}, {-1, 3, 6}, {0, 0, 1}, {0,1, 1}, {0, 1, 2}, {0, 1, 3}, {1, 1, 2}, {1, 1, 4}, {1, 2, 2}, {1,3, 3}, {1, 5, 7}};  

The resulting set of 111 lines and 111 points looks like the following:

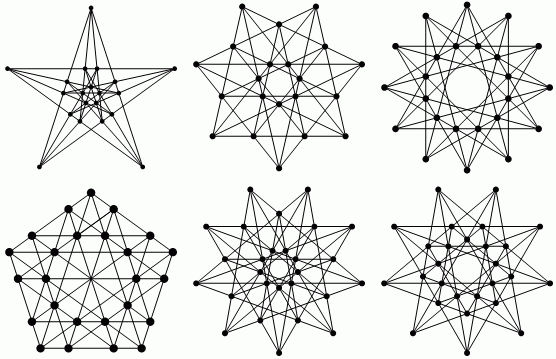
I'm not satisfied with that one yet. It needs a smaller set, and ideally there should be 6 lines through each point and 6 points on each line. Whether that's possible is actually an unsolved question in the realm of [configurations](https://en.wikipedia.org/wiki/Configuration_(geometry)). If every point has n lines and every line has n points it's known as an n-configuration. Here are some 4-configurations.

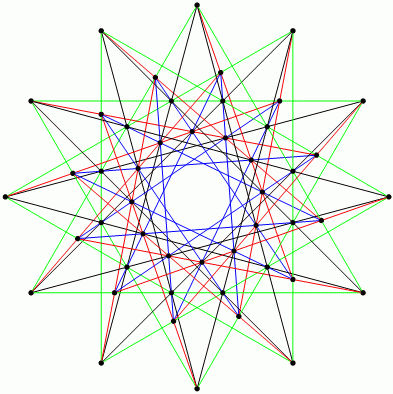
Whether a 5-configuration existed wasn't settled until 2007, when Leah Berman found the following:

Ideally, I should fold those configurations into barycentric coordinates and see if I could make improvements. Here are two more extreme orchards I found while searching in this space.

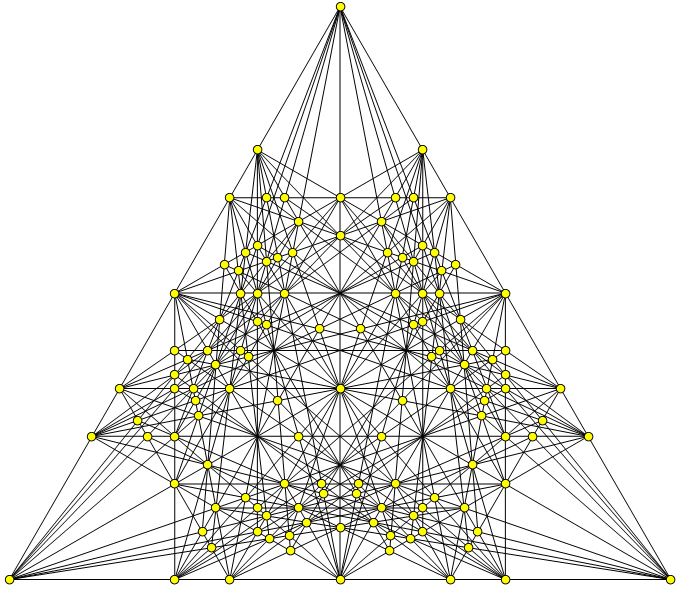
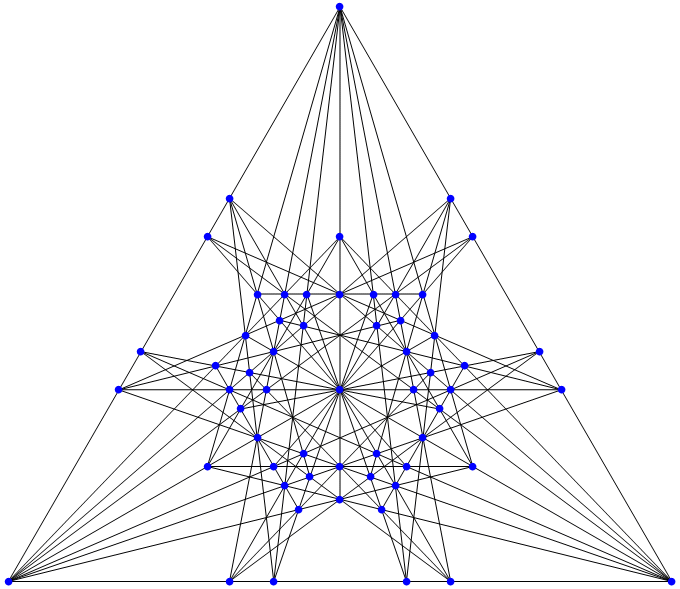
Can these be cleaned up to make the first 6-configuration, or beyond? Do all of the known best orchard solutions work out nicely in barycentric coordinates? With 30 trees, what is the maximal number of 3-lines, 4-lines, 5-lines, or 6-lines possible? All of these are unsolved questions. Based on my playing around here, I think that barycentric coordinates might lead to some new solutions in the world of extreme orchards.

Attachments:

ExtremeOrchardsF...nb