Last week, I participated in the
Zometool Workshop organized by Paul Hildebrandt for the
Simmetry Festival 2013, Delft. This was my first Zometool experience but it was like playing again with my favorite childhood toy

. My first idea was to build up a self-similar object with icosahedral symmetry, and then fill the remaining gaps in between:
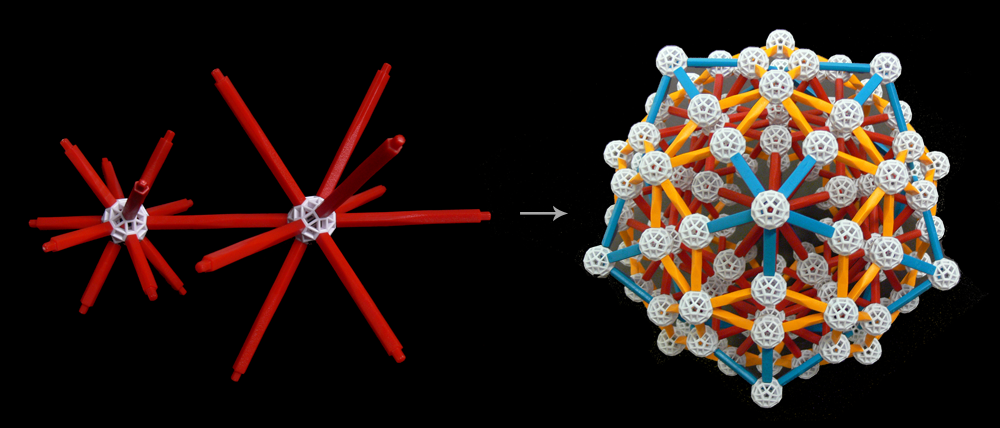
I had plenty of other ideas for new designs so I took the resulting sculpture back home. First I constructed a Golden Fractal Tree, then a Fullerene or a "soccer ball", and finally I ended up constructing a
Rhombic Triacontahedron and its closely related
Rhombic Hexecontahedron. To my surprise this last polyhedron appeared effortless in my hands, well, I suspect that the Wolfram|Alpha's logo has something to say about that ;-)
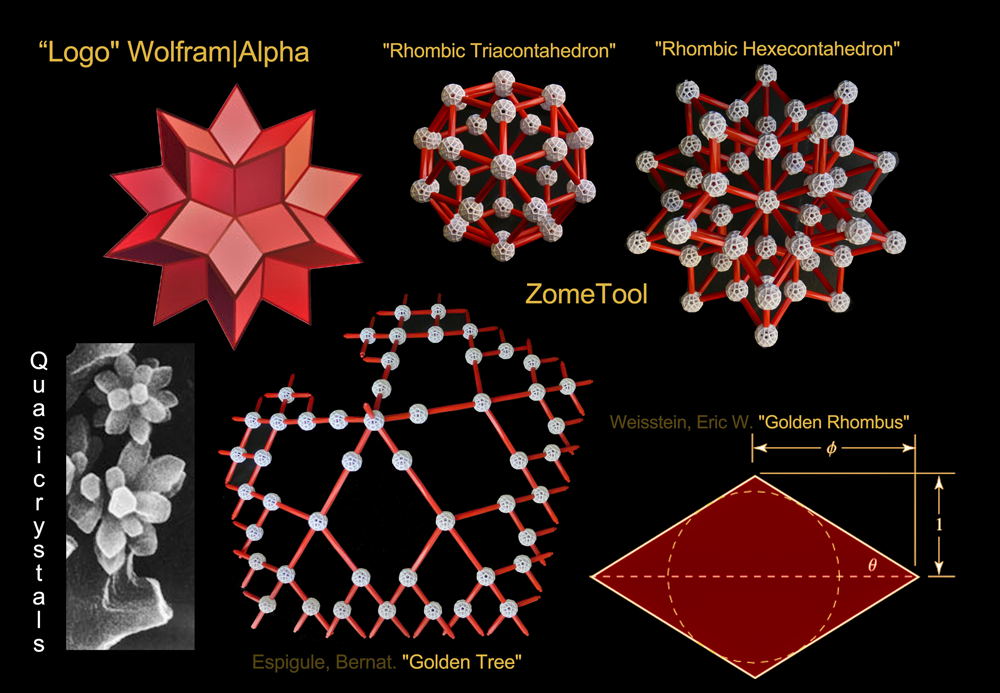
(The beautiful x-ray image of quasicrystals was taken from
the following blog post )
To conclude, the main idea to share with the Zometool enthusiasts is that
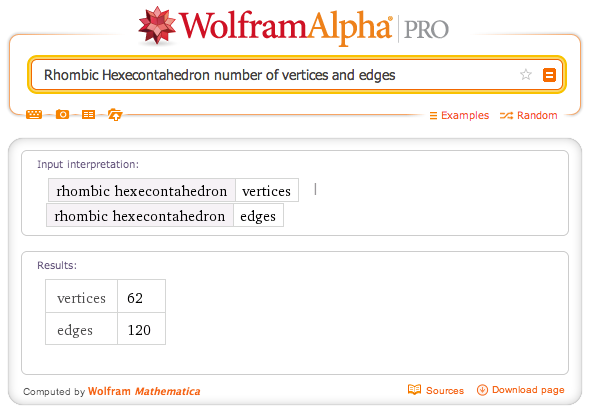
PolyhedronData in Mathematica or Wolfram|Alpha can be used wisely to gather the exact number of building blocks needed to construct your favorite polyhedron. For example the query
Rhombic Hexecontahedron number of vertices and edgestells us that we need 62 white balls and 120 red struts.
Finally, if you don't have access to Zometool you have still a chance to play with Rhombic Hexecontahedrons exploring the wonderful demonstrations submitted by
Sándor Kabai:
http://demonstrations.wolfram.com/search.html?query=Rhombic%20HexecontahedronP.S. I strongly recommend to read the fascinating WolframAlpha blog post by Eric W. Weisstein,
WHATS IN THE LOGO? THAT WHICH WE CALL A RHOMBIC HEXECONTAHEDRON and his MathWorld related entries
Golden Rhombus,
Rhombic Triacontahedron,
Rhombic Hexecontahedron and the famous
Spikey.