Tony Smith has a 4-dim Feynman Checkerboard Model that is referenced in Wikipedias Feynman Checkerboard article. Tony relates the Clifford Algebra gradings of his model to the number of one bits in Elementary Cellular Automata. In http://vixra.org/pdf/1611.0030v2.pdf, I used the Cartan subalgebra of the group theory in Tonys model to create this partitioning of the ECA rule space.
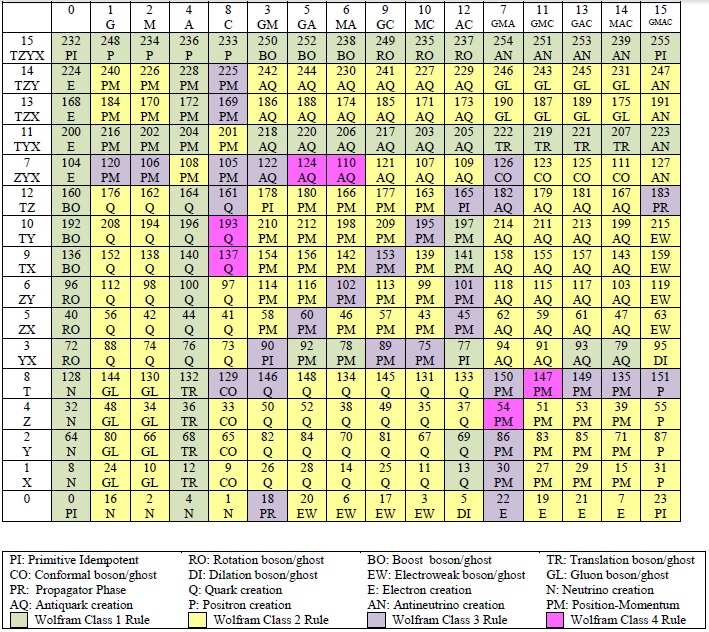
ECA rules seem like switches when used for links in Tonys Feynman Checkerboard model. Using ECA on links does fit with ECA being 1-dim and I can at least in part picture using ECA with a Feynman Checkerboard. Any thoughts on this rule space partitioning and on relating ECA rules to the Feynman Checkerboard and group theory would be welcome.