For some time now I have been interested in the idea of metaprogramming in the Wolfram Language. That WL lends itself to metaprogramming appeared so clear cut to me that I was surprised to find that the subject hasn't really come up in the community.
Not being a computer scientist (when I studied computer science at university, it was with the benefit of punched cards), I began to wonder if I had misapprehended something fundamental about WL. Happily, the talented Leonid Shifrin has taken a keen interest in the subject and written extensively about it, including this excellent post on Stack Exchange, in which he lays out the fundamental concepts. His view is that:
Mathematica is very well suited for meta-programming, and one can write much more powerful programs in Mathematica by utilizing it.
I will pick out a couple of the highlights here, but I would recommend a thorough reading of Leonid's post in its entirety.
Introspection
Writes Leonid:
Mathematica is IMO very strong here. There are a couple of reasons for this: Homoiconic language (programs written in own data structures - Mathematica expressions. This is code-as-data paradigm, like Lisp which uses lists for this) One can access global definitions for symbols stored in OwnValues, DownValues, SubValues, UpVaulues, etc, and various other global properties, programmatically. Rule-based destructuring techniques (using Cases etc) seriously simplify many introspection-related operations
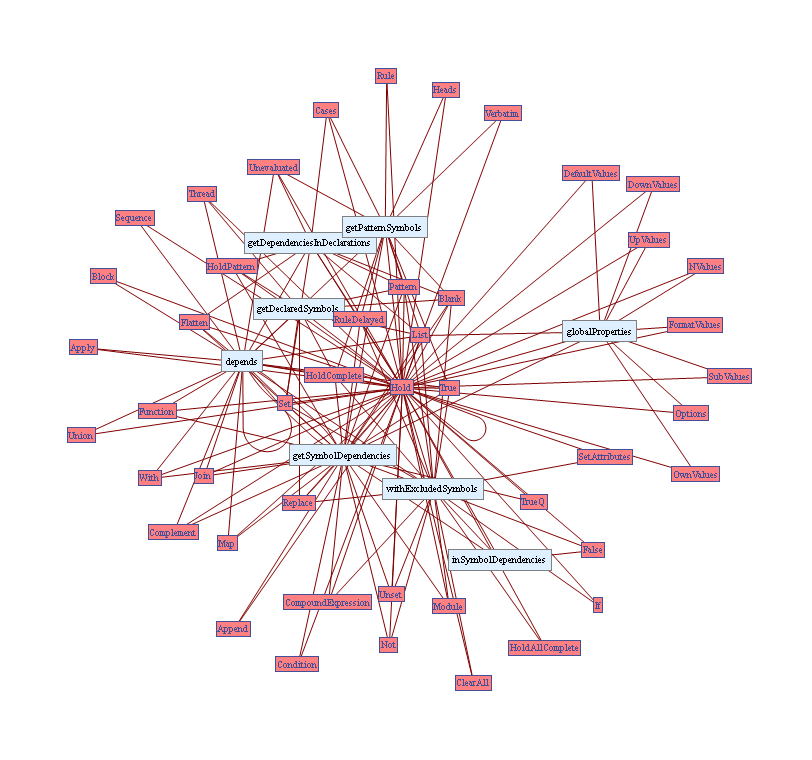
An excellent example of WL's capabilities is given in a related post on automatically generating a dependency graph of an arbitrary Mathematica function.
Run-time Code Generation
Leonid goes on to write about WL's capabilities in this type of metaprogramming, including making JIT-compiled functions. He gives the following example:
ClearAll[selectJIT];
selectJIT[pred_, listType_] :=
selectJIT[pred, Verbatim[listType]] =
Block[{lst},
With[{decl = {Prepend[listType, lst]}},
Compile @@
Hold[decl, Select[lst, pred], CompilationTarget -> "C",
RuntimeOptions -> "Speed"]]];
which is tested in the following example:
test = RandomInteger[{-25, 25}, {10^6, 2}];
selectJIT[#[[2]] > 0 &, {_Integer, 2}][test] // Short // AbsoluteTiming
selectJIT[#[[2]] > 0 &, {_Integer, 2}][test] // Short // AbsoluteTiming
(*
==> {0.4707032,{{-6,9},{-5,23},{-4,4},{13,3},{-5,7},{19,22},<<489909>>,{11,25},{-6,5},
{-24,1},{-25,18},{9,19},{13,24}}}
==> {0.1250000,{{-6,9},{-5,23},{-4,4},{13,3},{-5,7},{19,22},<<489909>>,{11,25},{-6,5},
{-24,1},{-25,18},{9,19},{13,24}}}
*)
The second time it was several times faster because the compiled function was memoized.
Macros
This is what is foremost in my mind when thinking about metaprogramming. Specifically, a macro in the context of WL means a construct which
- Manipulates pieces of Mathematica code as data, possibly preventing them from (premature) evaluation
- Expands code at run-time (not "read-time" or "compile-time", which are not so well defined in Mathematica)
Leonid offers several examples of WL metaprogramming macros in his own and other Stack Exchange posts that the reader is encouraged to explore. He also points out some of the deficiencies of WL in this context, which include hard to control evaluation and the lack of a clearly delineated compilation stage.
Wolfram Alpha for WL
Some limited metaprogramming capabilities for code generation are built into Wolfram Alpha. So, for instance, the Wolfram Alpha query Integrate Log(x) will produce not only the result,
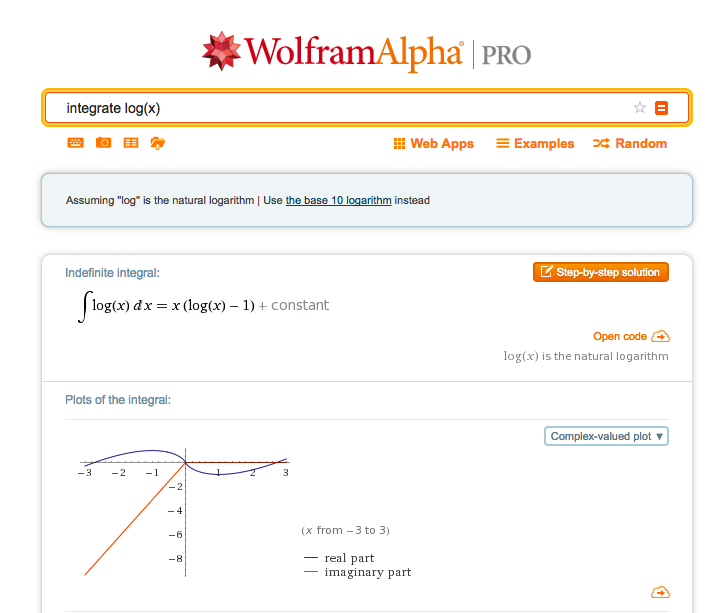
but also the appropriate WL code for evaluating the indefinite integral, i.e.
Integrate[Log[x], x]
But suppose we wanted some help to generate code to do something a little more complicated - say, for example, to solve one of the problems in Stephen Wolfram's Elementary Introduction to the Wolfram Language.
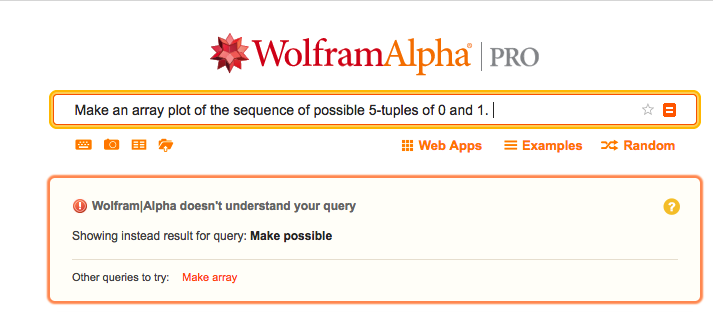
So how would one proceed to develop a more useful WL macro generator?
Before offering some suggestions and ideas, I'll press pause here in the hope of opening up the discussion - this is quite a long post already and I would like to gauge the level of interest in a continuation (if any!).