Group Abstract Group Abstract

Message Boards Message Boards

0
|
18.1K Views
|
4 Replies
|
2 Total Likes
View groups...
Share
Share this post:

Visualize triple integrals?

Mitchell Sandlin
Posted 9 years ago
Attachments:
POSTED BY: Mitchell Sandlin
4 Replies
Sort By:

Thanks so much, your explanation helps a lot. However, how would you plot the region of the integral if you wanting to integrate something more than just "1" (for volume). Say for example instead of integrating 1 you were integrating 3y. How would you incorporate the 3y into the "pred" along with the ranges? I tried several things trying to incorporate the 3*y and nothing that I tried seem to work.
POSTED BY: Mitchell Sandlin

You can try using NIntegrate to get integration sampling points and color for the function values.

sPnts = Reap[NIntegrate[1, {z, 0, 3}, 
       {x, 0, 4 - (4*z)/3}, 
       {y, 0, 2 - x/2 - (2*z)/3}, PrecisionGoal -> 6, 
     Method -> {"GaussKronrodRule", "Points" -> 12, 
       "SymbolicProcessing" -> 0}, 
     EvaluationMonitor :> Sow[{z, x, y}]]][[2, 1]];

Clear[f]
f[z_, x_, y_] := 3 y;
Graphics3D[
 MapThread[{Hue[#1], Point[#2]} &, {Rescale[f @@@ sPnts], sPnts}], 
 Axes -> True, AxesLabel -> {"z", "x", "y"}, 
 FaceGrids -> {{-1, 0, 0}, {0, 0, -1}}]

enter image description here
POSTED BY: Anton Antonov

Either 

r = ImplicitRegion[0 <= x <= 4 - (4*z)/3 && 0 <= y <= 2 - x/2 - (2*z)/3 && 
    0 <= z <= 3, {x, y, z}];
Integrate[3 y , {x, y, z} \[Element] r]

Or 

Integrate[3y Boole[
   0 <= x <= 4 - (4*z)/3 && 0 <= y <= 2 - x/2 - (2*z)/3 && 
    0 <= z <= 3], {x, -Infinity, Infinity}, {y, -Infinity, 
  Infinity}, {z, -Infinity, Infinity}]
POSTED BY: Emerson Willard

Everything you need to know is in the documentation. enter image description here

You need to represent your region as as a Boolean expression that defines the points in space that you want integrate over. This is your predicate and is the first argument of RegionPlot3D . The remaining arguments for x,y and z just specify what you will see when the plot is rendered.

RegionPlot3D[
 0 <= x <= 4 - (4*z)/3 && 0 <= y <= 2 - x/2 - (2*z)/3 && 0 <= z <= 3, {x, -1, 4}, {y, -1, 2}, {z, -1, 3}]

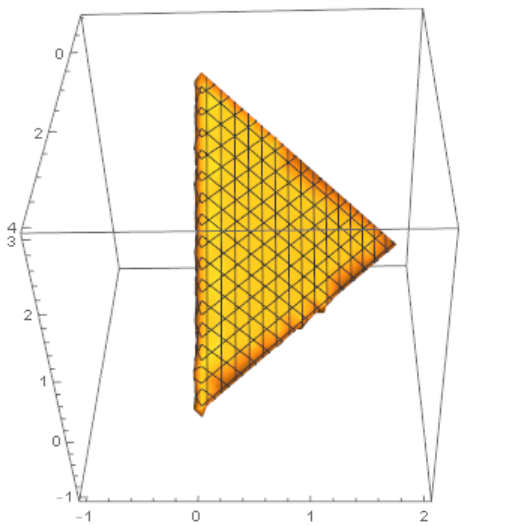enter image description here jj

Since your integral could represent a volume you can compute the volume of your implicit region.

r = ImplicitRegion[0 <= x <= 4 - (4*z)/3 && 0 <= y <= 2 - x/2 - (2*z)/3 &&  0 <= z <= 3, {x, y, z}];
RegionPlot3D@r
Volume@r

Alternatively, this very nice as well.

Integrate[1, {x, y, z} \[Element] r]

Or perhaps most economically

1/3*(1/2*4*2)*3
POSTED BY: Emerson Willard
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard