It is fairly straight forward to solve a Sudoku as an integer programming problem, by creating 9 binary variables for each cell, only one of which is one in the solution. The walk-through below and attached notebook illustrates this for the problem shown.
Implementation
Given values, as {row, column, value}
input = {
{1,4,4},{1,5,9},{1,8,5},{2,1,6},{2,5,3},{3,1,4},
{3,2,5},{3,4,6},{3,5,2},{3,7,3},{3,9,7},{4,1,5},
{4,3,2},{4,4,7},{4,7,9},{4,8,8},{5,1,3},{5,3,6},
{5,7,2},{5,9,1},{6,2,9},{6,3,1},{6,6,2},{6,7,6},
{6,9,5},{7,1,2},{7,3,5},{7,5,1},{7,6,4},{7,8,3},
{7,9,8},{8,5,8},{8,9,9},{9,2,1},{9,5,7},{9,6,3}};
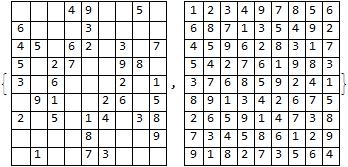
Display given values
viewmat = Table["", {9}, {9}];
Do[viewmat[[input[[i, 1]], input[[i, 2]]]] = ToString[input[[i, 3]]], {i, Length[input]}]
Grid[viewmat, Frame -> All]
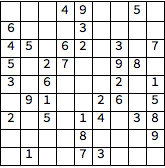
Variables, as 9 x 9 x 9 matrix
varmat = Table[m[i, j, k], {i, 9}, {j, 9}, {k, 9}];
Variables as a list
vars = Flatten[varmat];
Constrain the input cells to their value
cons1 = (varmat[[Sequence @@ #]] == 1 &) /@ input
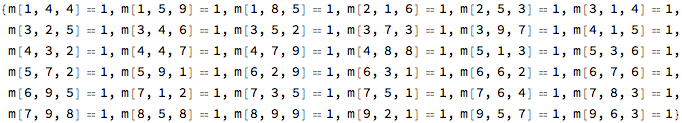
The sum of the binary variables for each cell is 1
cons2 = Flatten @ Table[ (Sum[varmat[[i, j, k]], {k, 9}] == 1), {i, 9}, {j, 9}];
All different constraint for the rows
cons3 = Flatten @ Table[ (Sum[varmat[[i, j, k]], {i, 9}] == 1), {j, 9}, {k, 9}];
All different constraint for the columns
cons4 = Flatten @ Table[ (Sum[varmat[[i, j, k]], {j, 9}] == 1), {i, 9}, {k, 9}];
All different constraint for the submatrices
sm[di_, dj_] := Flatten [Table[{i, j}, {i, 1 + 3*(di - 1), 3*di}, {j, 1 + 3*(dj - 1), 3*dj}],1]
cons5 = Flatten @ Table[(Total[m[Sequence @@ #, k] & /@ sm[i, j]] == 1), {i, 3}, {j, 3}, {k, 9}];
Confine the variables to the range 0 to 1
cons6 = Thread[0 <= vars <= 1];
Combine the constraints
Length[allcons = Join[cons1, cons2, cons3, cons4, cons5, cons6]]
1089
Solve the problem, specifying that the variables are integers.
AbsoluteTiming[sol = FindMinimum[{0, allcons, Element[vars, Integers]}, vars];]
{0.0946335, Null}
Find the values for each cell
resmat = Table[Sum[k*m[i, j, k], {k, 9}], {i, 9}, {j, 9}] /. sol[[2]]

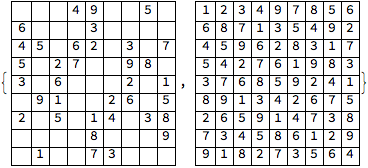
Display the input and result
{Grid[viewmat, Frame -> All], Grid[resmat, Frame -> All]}
Check the result
And @@ Table[Unequal[Sequence @@ resmat[[i]]], {i, 9}]
True
And @@ Table[Unequal[Sequence @@ Transpose[resmat][[i]]], {i, 9}]
True
And @@ Flatten @ Table[Unequal[resmat[[Sequence @@ #]] & /@ sm[i, j]], {i, 3}, {j, 3}]
True
 Attachments:
Attachments: