Hi,
My Problem is probably pretty straight forward. I have an equation I cannot solve by hand, so I asked WA. My initial attempt (after getting rid of some errors of mine) was the following:
Solve[0 ==1.33- (0,059/6)*Log10[ ((X/60)^2)/(((25-7*X+10^(-7))/60)^14*0.5*X)]-(-0.43-0.0295*Log10[1/((25+5.9-1.5*X)/60)]),X]
Which produced the error-message:
Solve::inex: Solve was unable to solve the system with inexact coefficients or the system obtained by direct rationalization of inexact numbers present in the system. Since many of the methods used by Solve require exact input, providing Solve with an exact version of the system may help.
As ´0,059/6` is real and not rational I exchanged it with 0.00983 which should be sufficiently precise for my purposes. Tried it again, but nothing changed. When using the following in order to have that request computed by WA directly I got the value 3.57143 which I was mildly happy about, as it was a solution although I didn't quite like the result. (I had expected something in the magnitude of 5.)
==Solve[0 ==1.33- 0.00983*Log10[ ((X/60)^2)/(((25-7*X+10^(-7))/60)^14*0.5*X)]-(-0.43-0.0295*Log10[1/((25+5.9-1.5*X)/60)]),X]
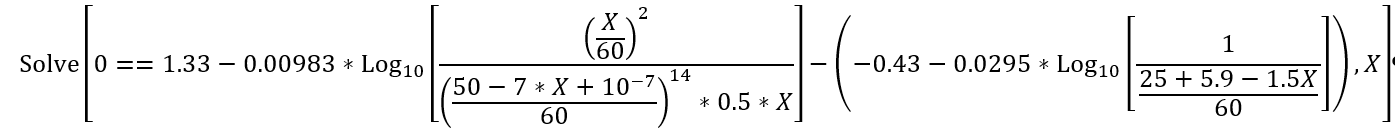
Same formula as a picture for better overview.
My Joy was further diminished when I noticed I made a mistake in my formula. This should be the right time to explain what I was originally trying to calculate.
As I am a chemist I wanted to solve a problem concerning a redox reaction. An amount of Oxalat, acid and Dichromate are solved in water, the volume of the solution is 60 mL. I did that and wondered why I didn't get more product (Potassiumchrome(III)oxalat). What exactly happened isn't really the point here, but this was the foundation of my equation.
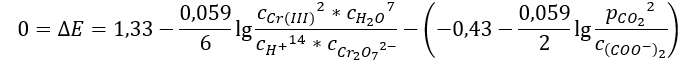
After some simplifications and the substitution of different parameters as a function of X, which I defined as the amount of Cr(III) [mol] I got said formula. Well, I got the above formula, the correct formula should have been:
Solve[0==1.33-0.00983* Log10[((X/60)^2)/(((25-7*X+10^(-7))/60)^14*( *(4.1-0.5*X)/60)* )] -(-0.43-0.0295* Log10[1/((25+5.9-1.5*X)/60)]), X] (the change is *(4.1-0.5 X)/60)*)
This got the now familiar error-message "Solve::inex". Trying again to have that computed by WA led me to being told that the runtime of 30 seconds was exceeded:
WolframAlpha::timeout: The call to WolframAlpha[Solve[0 == 1.33 - 0.00983Log10[((X/60)^2)/(((25 - 7X + 10^(-7))/60)^14( (4.1 - 0.5X)/60))] - (-0.43 - 0.0295Log10[1/((25 + 5.9 - 1.5X)/60)]), X]] has exceeded 30.` seconds. Increasing the value of the TimeConstraint option may improve the result.
So I found out how to do that and tried:
==TimeConstrained[Solve[0==1.33-0.00983* Log10[((X/60)^2)/(((25-7*X+10^(-7))/60)^14*((4.1-0.5*X)/60))] -(-0.43-0.0295* Log10[1/((25+5.9-1.5*X)/60)]), X], 300]
FetchURL::httperr: The request to URL http://www4c.wolframalpha.com/api/v2/recalc.jsp?appid=XXX&id=XXX&uuid=None&mlicense=XXX&machineid=XXX&sig=XXX was not successful. The server returned the HTTP status code 403 ("Forbidden").
[I XXXed out the IDs. Don't know if they mean anything to any of you, but I prefer being cautious.]
Not really suprising that WA prohibits that, but well, worth a try. Next I tried out multiple versions of N[XXX, 5], which were all pretty useless not to say stupid of me. I played around with Solve[expr,X,Reals], which didn't lead to anything. After that I found a NSolve[], and well, a numerical solution would be perfectly fine with me, but it didn't work out. I was considering to split it up and get some expression for each logarithm. I wasn't able to do that, as for Solve[ ] I need an equation and I couldn't get my head around that. Simplify[ ] didn't yield anything.
And now I'm out of ideas... Is the equation even solvable? In my inexperienced opinion I'd say if I got a solution for the "wrong" equation, I should get one for the second one, too, as it isn't that much more complicated...
I'd be happy if some of you had an idea you could share with me, point out some mistakes of mine or help me in any other way. It buggs me not knowing why it doesn't work and probably even more not knowing how to fix it...
Thank you all in advance and have a nice day!
J
Edit: I've jet to get accustomed to the formatting and editing in this forum, eg. the §§-thingies. So please be patient with me if I didn't do it well. That's why I inserted the two formulas as pictures. In case I broke some code of conduct rules, please tell me I'll try better next time I'm around. If you need more information of any kind I'd be glad to provide them. Edit 2: Damn it, got rid of some typos.