Group Abstract Group Abstract

Message Boards Message Boards

Solve Redox equation with inexact coefficients, Solve[Log10[f(x)]]?

Jonas N., Student
Posted 9 years ago

Hi,

My Problem is probably pretty straight forward. I have an equation I cannot solve by hand, so I asked WA. My initial attempt (after getting rid of some errors of mine) was the following:

Solve[0 ==1.33- (0,059/6)*Log10[ ((X/60)^2)/(((25-7*X+10^(-7))/60)^14*0.5*X)]-(-0.43-0.0295*Log10[1/((25+5.9-1.5*X)/60)]),X]

Which produced the error-message:

Solve::inex: Solve was unable to solve the system with inexact coefficients or the system obtained by direct rationalization of inexact numbers present in the system. Since many of the methods used by Solve require exact input, providing Solve with an exact version of the system may help.

As ´0,059/6` is real and not rational I exchanged it with 0.00983 which should be sufficiently precise for my purposes. Tried it again, but nothing changed. When using the following in order to have that request computed by WA directly I got the value 3.57143 which I was mildly happy about, as it was a solution although I didn't quite like the result. (I had expected something in the magnitude of 5.)

 ==Solve[0 ==1.33- 0.00983*Log10[ ((X/60)^2)/(((25-7*X+10^(-7))/60)^14*0.5*X)]-(-0.43-0.0295*Log10[1/((25+5.9-1.5*X)/60)]),X]

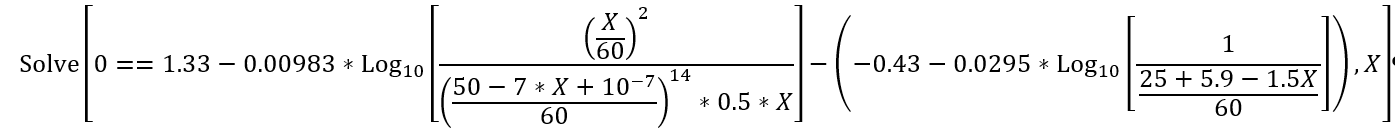
Same formula as a picture for better overview
Same formula as a picture for better overview.

My Joy was further diminished when I noticed I made a mistake in my formula. This should be the right time to explain what I was originally trying to calculate.
As I am a chemist I wanted to solve a problem concerning a redox reaction. An amount of Oxalat, acid and Dichromate are solved in water, the volume of the solution is 60 mL. I did that and wondered why I didn't get more product (Potassiumchrome(III)oxalat). What exactly happened isn't really the point here, but this was the foundation of my equation.

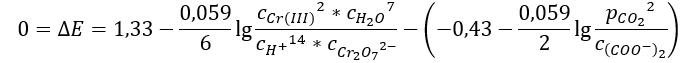
Nernst equasion

After some simplifications and the substitution of different parameters as a function of X, which I defined as the amount of Cr(III) [mol] I got said formula. Well, I got the above formula, the correct formula should have been:

Solve[0==1.33-0.00983* Log10[((X/60)^2)/(((25-7*X+10^(-7))/60)^14*(   *(4.1-0.5*X)/60)*   )] -(-0.43-0.0295* Log10[1/((25+5.9-1.5*X)/60)]), X]    (the change is  *(4.1-0.5 X)/60)*)

This got the now familiar error-message "Solve::inex". Trying again to have that computed by WA led me to being told that the runtime of 30 seconds was exceeded:

WolframAlpha::timeout: The call to WolframAlpha[Solve[0 == 1.33 - 0.00983Log10[((X/60)^2)/(((25 - 7X + 10^(-7))/60)^14( (4.1 - 0.5X)/60))] - (-0.43 - 0.0295Log10[1/((25 + 5.9 - 1.5X)/60)]), X]] has exceeded 30.` seconds. Increasing the value of the TimeConstraint option may improve the result.

So I found out how to do that and tried:

==TimeConstrained[Solve[0==1.33-0.00983* Log10[((X/60)^2)/(((25-7*X+10^(-7))/60)^14*((4.1-0.5*X)/60))] -(-0.43-0.0295* Log10[1/((25+5.9-1.5*X)/60)]), X], 300]

FetchURL::httperr: The request to URL http://www4c.wolframalpha.com/api/v2/recalc.jsp?appid=XXX&id=XXX&uuid=None&mlicense=XXX&machineid=XXX&sig=XXX was not successful. The server returned the HTTP status code 403 ("Forbidden").
[I XXXed out the IDs. Don't know if they mean anything to any of you, but I prefer being cautious.]

Not really suprising that WA prohibits that, but well, worth a try. Next I tried out multiple versions of N[XXX, 5], which were all pretty useless not to say stupid of me. I played around with Solve[expr,X,Reals], which didn't lead to anything. After that I found a NSolve[], and well, a numerical solution would be perfectly fine with me, but it didn't work out. I was considering to split it up and get some expression for each logarithm. I wasn't able to do that, as for Solve[ ] I need an equation and I couldn't get my head around that. Simplify[ ] didn't yield anything.

And now I'm out of ideas... Is the equation even solvable? In my inexperienced opinion I'd say if I got a solution for the "wrong" equation, I should get one for the second one, too, as it isn't that much more complicated...

I'd be happy if some of you had an idea you could share with me, point out some mistakes of mine or help me in any other way. It buggs me not knowing why it doesn't work and probably even more not knowing how to fix it...

Thank you all in advance and have a nice day!

J

Edit: I've jet to get accustomed to the formatting and editing in this forum, eg. the §§-thingies. So please be patient with me if I didn't do it well. That's why I inserted the two formulas as pictures. In case I broke some code of conduct rules, please tell me I'll try better next time I'm around. If you need more information of any kind I'd be glad to provide them. Edit 2: Damn it, got rid of some typos.

POSTED BY: Jonas N.
9 Replies
Sort By:

Hi,

this here appears to work on WA. It does time out but you do see two (very similar) solutions. I would recommend though to use one of the free versions of the Wolfram Language in the cloud, such as the Wolfram Development Platform. There you can use standard Wolfram Language code:

sols=NSolve[0 == 1.33 - (0.059/6)*Log10[((X/60)^2)/(((25 - 7*X + 10^(-7))/60)^14*0.5*X)] - (-0.43 - 
0.0295*Log10[1/((25 + 5.9 - 1.5*X)/60)]), X, Reals, WorkingPrecision -> 30]

If you substitute that into the original equation it seems to work:

1.33 - (Rationalize[0.059]/6)*Log10[((X/60)^2)/(((25 - 7*X + 10^(-7))/60)^14*1/2*X)] - (-Rationalize[0.43] - 
Rationalize[0.0295]*Log10[1/((25 + Rationalize[5.9] - 3/2*X)/60)]) /. sols

Gives two "numerical zeros".

Cheers,

Marco
POSTED BY: Marco Thiel
Jonas N.
Jonas N., Student
Posted 9 years ago

Hello Bill.

Yes, that might have been an option, you are right. I'm sorry. But I was under the impression, that asking for a specific problem was better than posting my general problem and expecting someone to solve it for me. And I really did hope to learn enough to solve it myself, as I'm probably the only one who cares if I solve this (or if it is solved at all).

And I just got almost exactly the same solution in a completely different way. Which kinda impresses me, because I thought my original equation was not precise enough to mimic my Problem. Thank you for your effort!

What I did in the end was:

Clear[a, d]
a[x_] = 1.76` + (26691 Log[1/60 (30.9 - 1.5` x)])/(6.25*10^7) -
    (2135281 Log[x^2/ ( 3600 (Sqrt[10^-14 + 1/4 (-(5/6) + (7 x)/60)^2] + 1/2 (5/6 - (7 x)/60))^14 (4.1` - 0.5` x))] ) / (5*10^8)
d[x_] = D[a[x], x]
FindMinimum[{d[x], 1 < x < 8}, {x, 7.14}]
Plot[a[x], {x, 0.01, 8}, PlotRange -> {0.2, 2}]
Clear[a, d]

I got a new equation and found it's inflection point. I did find the root, too, but I preferred this one.

I know it's a bit late in the end, but I could explain my original problem:

The reaction of Potassium Dichromate with Oxalic Acid and Potassium Oxalate to Carbon Dioxide and Chrome(III) is highly influenced by the concentration of Protons (pH), although there are different possibilities which of the reagents (/educts) is the limiting factor. I had used 4.1 mmol <code>K_2Cr_2O_7, 25 mmol <code>(COOH)_2 and 5.9 mmol <code>K_2(COO)_2. My Volume had been 60 mL. With the Nernst-Equation you can calculate the redox-potential of a redoxreaction and therefor whether or not a reaction takes place. After listing a lot of factors I wanted to disregard or assumptions I wanted (had) to make I set up an equation and tried to solve it with Mathematica. Formulas and my final computable Formula:
My reactions
Equation

And thanks to your help, too, I am not only able to take a very good educated guess (only guessing because of all of those assumptions) when the reaction stopped, I am able to show that it indeed is because of the pH. (As a nice side-effect I also justified some of my assumptions.) The following shows a plot of the pH and the redoxpotential.

pH-Redox

I also understand now why the root you provided (have I thanked you for that yet?) is the same to my result. My original approach was only able run to a pH of 7, the pH of at my inflection point is 7.

I wanted to tell you that I am very thankful for your patience with me. And for helping me learn a great deal today.
Sincerely Yours,
Jonas
POSTED BY: Jonas N.
Bill Simpson
Bill Simpson
Posted 9 years ago
POSTED BY: Bill Simpson
Jonas N.
Jonas N., Student
Posted 9 years ago
POSTED BY: Jonas N.
Jonas N.
Jonas N., Student
Posted 9 years ago
POSTED BY: Jonas N.
Jonas N.
Jonas N., Student
Posted 9 years ago

Thank you Bill,

Yesterday evening I tried the Plot[ ], too, but sadly it didn't lead to a solution I was satisfied with...

Both, the find root and the plot give back the result 3.57[...], which was my original result. As I looked at the Formula noticed that it was using my original mistaken one and not the "revised" version.

Thanks for your effort!
POSTED BY: Jonas N.
Bill Simpson
Bill Simpson
Posted 9 years ago

Try this

WA Plot

followed by

WA FindRoot
POSTED BY: Bill Simpson
Jonas N.
Jonas N., Student
Posted 9 years ago

Ok, thanks, now I at least understand why it wouldn't compute. Could you give me some kind of advice on how to get

Log10[(369720589101871337890625 X^2)/((500000001/10000000 - 7 X)^14 (4.1 - 0.5 X))]

to be either? I'm assuming to get that to be an integer is pretty unrealistic. Is there a chance to get it to be a fraction? My initial idea was rounding that, but it failed. Probably because you can't round variables...
POSTED BY: Jonas N.

When Solve wants rational numbers it means integers or fractions.
POSTED BY: Frank Kampas
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard