Group Abstract Group Abstract

Message Boards Message Boards

1
|
11.7K Views
|
11 Replies
|
8 Total Likes
View groups...
Share
Share this post:

[?] Plot an Archimedean Spiral with equidistant points?

Nikki Peter
Posted 8 years ago

Hi

has somebody experience with the Archimedean Spiral? In general it is quite simple to create an Archimedean Spiral by e.g. a line function. I rather want to create a spiral with equidistant points. The amount of the "sampling" points should be adjustable. I saw some examples, but I could not follow it, for example:

Equation to place points equidistantly on an Archimedian Spiral using arc-length

I created following code so far:

a = 0.75;
K = 3;
L1 = 90; 
rp = 0.0; 

alpha = L1*Pi/180;

Sample = 80;   (* sampling per azimuth direction *)
M = 1;                  (* number of spirals *)

x1[t_, m_] := (rp*Cos[alpha]) + a*t*Cos[t + (m*2*Pi/M)];
y1[t_, m_] := (rp*Sin[alpha]) + a*t*Sin[t + (m*2*Pi/M)];

data1 = Table [{x1[t, m], y1[t, m]}, {t, 0, K*2 \[Pi], 
2 \[Pi]/Sample}, {m, 1, M}];

dataflat1 = Flatten[data1, 1];

Graphics[{Thick, Blue, PointSize[0.0075], Point[dataflat1]},  Axes -> True, AxesLabel -> {X, Y}]

enter image description here
POSTED BY: Nikki Peter
11 Replies
Sort By:
Nikki Peter
Nikki Peter
Posted 8 years ago

Hi all,

thank you for your replies. It's been quite some time since I started my request. Now, I would appreicate some help again :-). I want to use the same code as M. Rogers proposed above. The poiints I get from

points = Table[{x1[t, 0], y1[t, 0]}, {t, tdata}];

shall be used for a further caluclation..and now I'm struggling with my mathematica skills.

I have to use following equation. This equation describes the Fraunhofer-diffraction. But I get an error by using "ponts": I Just need to sum all points which are generated in "tdata"

\[Lambda] = 1.0 ;
Dfar = 1.0 ;
delta = 20;
Nplot = 50;

faramp = \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(t = 0\), \(tdata\)]
\*SuperscriptBox[\(E\), \(
\*FractionBox[\(I\ 2  \[Pi]\), \(\[Lambda]\ Dfar\)] \((\((x*
         x1[t, 0])\) + \((y*y1[t, 0])\))\)\)]\) ;


intensityfar = (Re[faramp])^2 + (Im[faramp])^2;
DensityPlot[intensityfar, {x, -4/delta, 4/delta}, {y, -4/delta, 
  4/delta}, PlotPoints -> Nplot, PlotRange -> Automatic, 
 ColorFunction -> GrayLevel, Frame -> False, Exclusions -> None]
POSTED BY: Nikki Peter

The function f = nInvArcLength[param, {t, a, b}] returns a function f (an InterpolatingFunction) that computes the value of t = f[s] for a point that is a given arclength distance s along the parametrization param from the initial point at t == a. (This function works for parametrizations of curves in any dimension.) The domain of the function f can be queried since it is an InterpolatingFunction, and the domain the interval from 0 to the arclength of the curve.

ClearAll[nInvArcLength];
nInvArcLength::diff = "Parametrization `` not differentiable with respect to ``.";
nInvArcLength[param_?VectorQ, {t_, a_?NumericQ, b_?NumericQ}] := 
  Module[{time, s, v, realnorm = Sqrt[#.#] &},
   Check[   (* check for user-error: is param differentiable? *)
    v = D[param, t],
    Message[nInvArcLength::diff, param, t]];
   NDSolveValue[{
      time'[s] == 1/realnorm[v] /. t -> time[s], time[0] == a,
      WhenEvent[time[s] > b, "StopIntegration"]},
     time, {s, 0, Infinity}
     ] /; FreeQ[v, D]  (* The condition (/;) prevents NDSolveValue from running if `D` failed *)
   ];

For the OP's case, I call the function ts:

ts = nInvArcLength[{x1[t, 0], y1[t, 0]}, {t, 0, K * 2 Pi}]
(*  InterpolatingFunction[{{0., 134.788}}, << 4 >>]  *)

First@ts["Domain"]  (* the domain is 0 to the arclength of the whole path *)
(*  {0., 134.788}  *)

tdata = ts[Array[# &, K*Sample, First@ts["Domain"]]]; (* t-values for K*Sample evenly arclength-spaced points *)
points = Table[{x1[t, 0], y1[t, 0]}, {t, tdata}];    (* the corresponding points *)

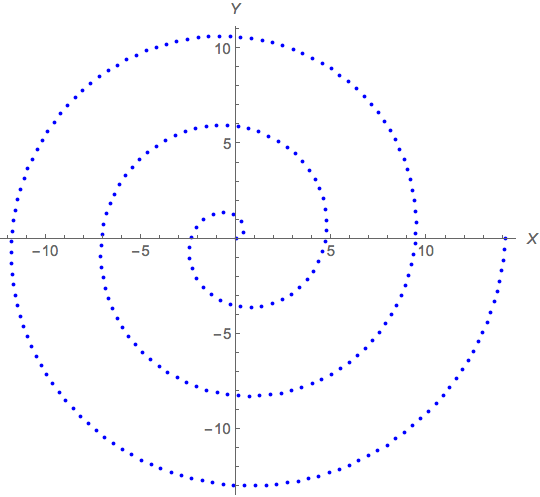
Graphics[{Thick, Blue, PointSize[0.0075], Point[points]}, Axes -> True, AxesLabel -> {X, Y}]

enter image description here
POSTED BY: Michael Rogers
Nikki Peter
Nikki Peter
Posted 8 years ago

Hi, many thanks for your replies!! The "Arclength" function is really very interesting. But I have not yet reached my target, unfortunately.

I need beside the plot also each x and y value of the specific points (here the content of my "dataflat1") for my further calculation. That's why I have started to create the code as mentioned above. So, finally I will try to incorporate the "arclength" function.....unless there is another kind of possibility..:-)
POSTED BY: Nikki Peter

There's the MeshFunction setting "ArcLength:

ParametricPlot[{x1[t, 0], y1[t, 0]}, {t, 0, K*2 \[Pi]}, 
 PlotStyle -> None, Mesh -> K*Sample - 2, 
 MeshFunctions -> {"ArcLength"}, MeshStyle -> Blue, 
 Epilog -> {Blue, Point[{x1[#, 0], y1[#, 0]} & /@ {0, K*2 Pi}]}]

Note that K is used internally by Mathematica for dummy variables. Setting it (or other single-letter variables) equal to a value is probably not a good idea. In general, I avoid starting names with capital letters, so that my functions and variables cannot conflict with the built-in functions and variables.
POSTED BY: Michael Rogers

enter image description here

Something like that? There is a built in sampling option that produces equidistant mesh points in 2D and 3D plots. The options is:

MeshFunctions->{"ArcLength"}

This is code you can hopefully start from (for animation above):

Manipulate[
    ParametricPlot[
       {u Sin[u],u Cos[u]},{u,0,12Pi},
       PerformanceGoal->"Quality",
       PlotTheme->"Marketing",
       MeshStyle->Directive[White,Opacity[.8],PointSize[.03]],
       Mesh->points (* number of points *),
       MeshFunctions->{"ArcLength"} (* equidistant points option *) ],
{{points,80},1,100,1,Appearance->"Labeled"}]
POSTED BY: Vitaliy Kaurov

MeshFunctions->{"ArcLength"}

Vey nice! Is this documented?
POSTED BY: Szabolcs Horvát

I am actually not sure, I simply knew it ;-)
POSTED BY: Vitaliy Kaurov

This MeshFunctions specification is mentioned here (along with "CurveLength"):

http://community.wolfram.com/groups/-/m/t/29463

It would be nice to add this to the documentation.
POSTED BY: Szabolcs Horvát

Vitaliy,

Oops, when I started my answer, yours had not appeared. I got drawn away by a hurricane-related problem for a few hours, and when I returned to finish my post, I thought there was just Szabolcs' answer. (I had left the old page up with a half-finished answer.)
POSTED BY: Michael Rogers

No worries ))
POSTED BY: Vitaliy Kaurov

How about simply PolarPlot[t, {t, 0, 20 Pi}]? It uses adaptive sampling to give you a high quality output. Or are the specific sampling points important to you?
POSTED BY: Szabolcs Horvát
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard