The function f = nInvArcLength[param, {t, a, b}] returns a function f (an InterpolatingFunction) that computes the value of t = f[s] for a point that is a given arclength distance s along the parametrization param from the initial point at t == a. (This function works for parametrizations of curves in any dimension.) The domain of the function f can be queried since it is an InterpolatingFunction, and the domain the interval from 0 to the arclength of the curve.
ClearAll[nInvArcLength];
nInvArcLength::diff = "Parametrization `` not differentiable with respect to ``.";
nInvArcLength[param_?VectorQ, {t_, a_?NumericQ, b_?NumericQ}] :=
Module[{time, s, v, realnorm = Sqrt[#.#] &},
Check[ (* check for user-error: is param differentiable? *)
v = D[param, t],
Message[nInvArcLength::diff, param, t]];
NDSolveValue[{
time'[s] == 1/realnorm[v] /. t -> time[s], time[0] == a,
WhenEvent[time[s] > b, "StopIntegration"]},
time, {s, 0, Infinity}
] /; FreeQ[v, D] (* The condition (/;) prevents NDSolveValue from running if `D` failed *)
];
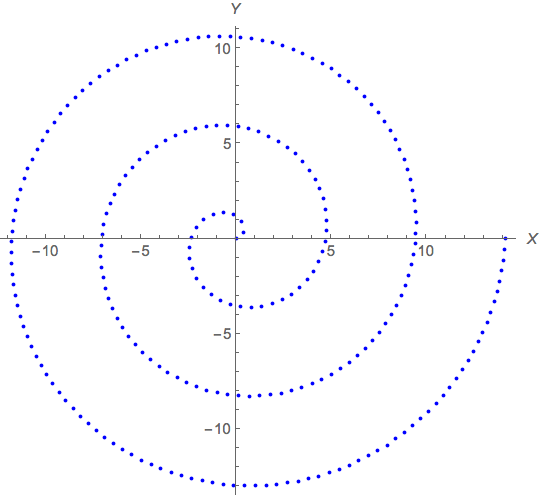
For the OP's case, I call the function ts:
ts = nInvArcLength[{x1[t, 0], y1[t, 0]}, {t, 0, K * 2 Pi}]
(* InterpolatingFunction[{{0., 134.788}}, << 4 >>] *)
First@ts["Domain"] (* the domain is 0 to the arclength of the whole path *)
(* {0., 134.788} *)
tdata = ts[Array[# &, K*Sample, First@ts["Domain"]]]; (* t-values for K*Sample evenly arclength-spaced points *)
points = Table[{x1[t, 0], y1[t, 0]}, {t, tdata}]; (* the corresponding points *)
Graphics[{Thick, Blue, PointSize[0.0075], Point[points]}, Axes -> True, AxesLabel -> {X, Y}]