I just read a blog post on
Defining and filling holes on the border of an image on
Steve on Image Processing which is about removing image holes including those connected to the image boundary.
The way the solution is formulated is by assuming that holes that are connected to the borders, are black regions that are connected to either of the two adjacent border (e.g. Left and Top, or Top and Right, etc).
This is our version of their image:
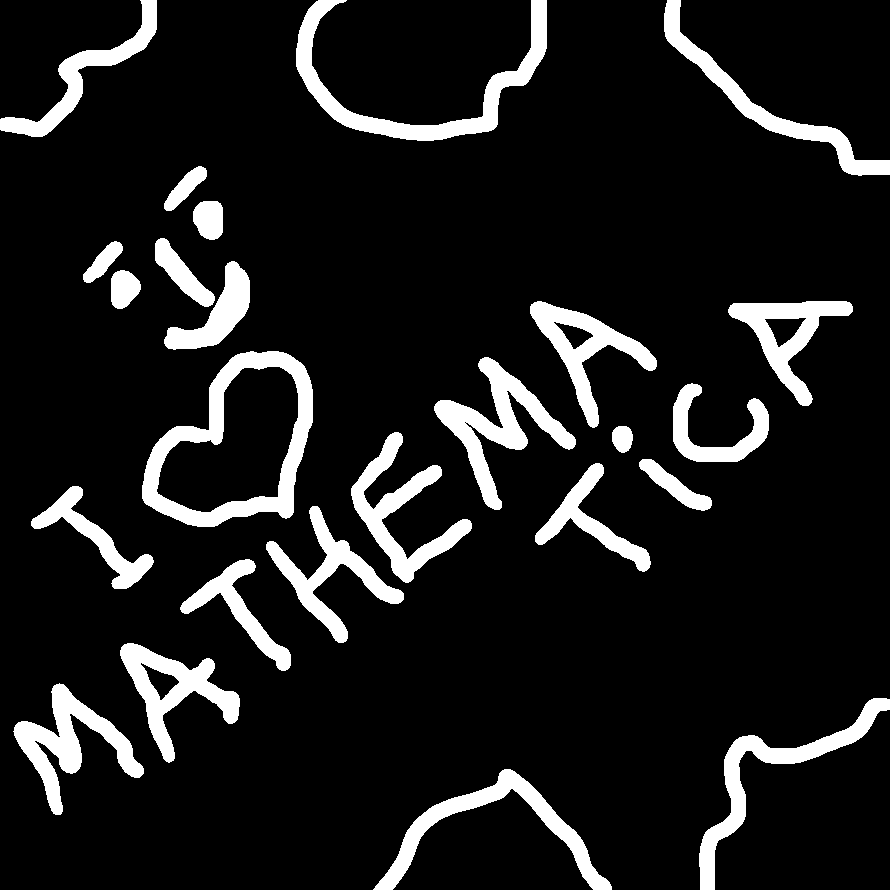
I wondered how and how easily this task can be done in Mathematica and here are my two simple solutions:
1) If all holes (both those entirely inside and those connected to the border) are small, one could use
DeleteSmallComponents on negated image and add negate to get the filled image. So:
ColorNegate@DeleteSmallComponents[ColorNegate[i]]
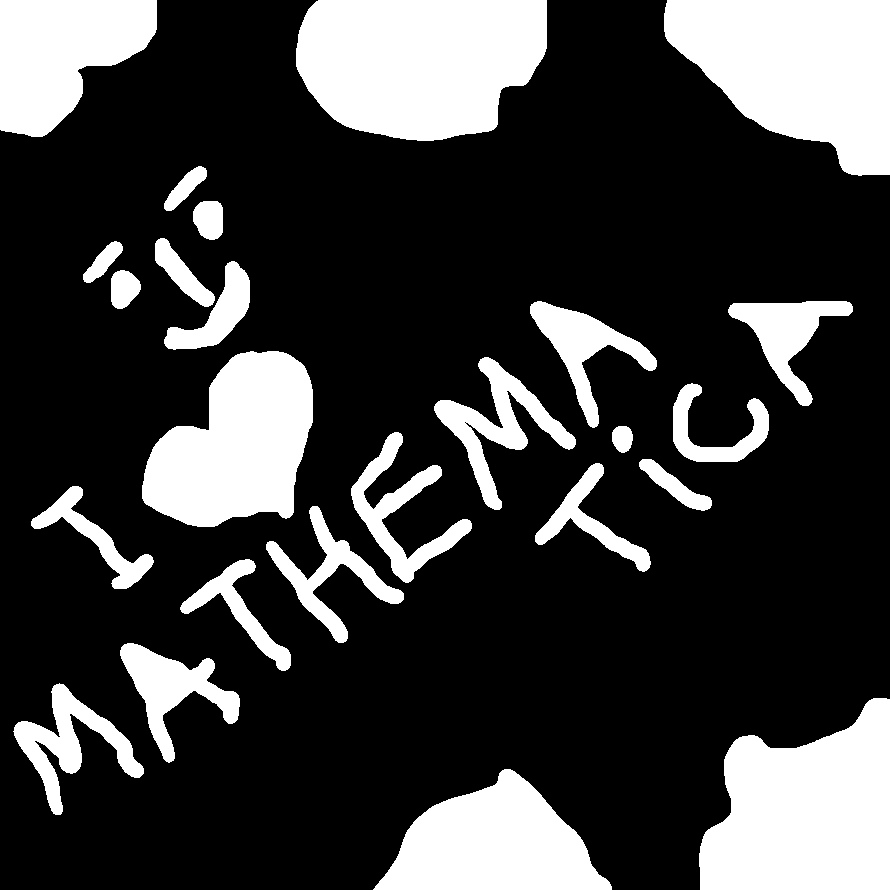
2) Second solution would be to (almost) implement the idea that Steve has implemented. Almost, since I chose an even simpler approach. On a negated image, I use
SelectComponents and pick all components that are connected to 2 or fewer borders. This will return all holes, both internal holes as well as those connected to the at most two borders. Add the result to the original image to get the holes filled:
ImageAdd[i,
SelectComponents[ColorNegate[i], "AdjacentBorderCount", # <= 2 &]]
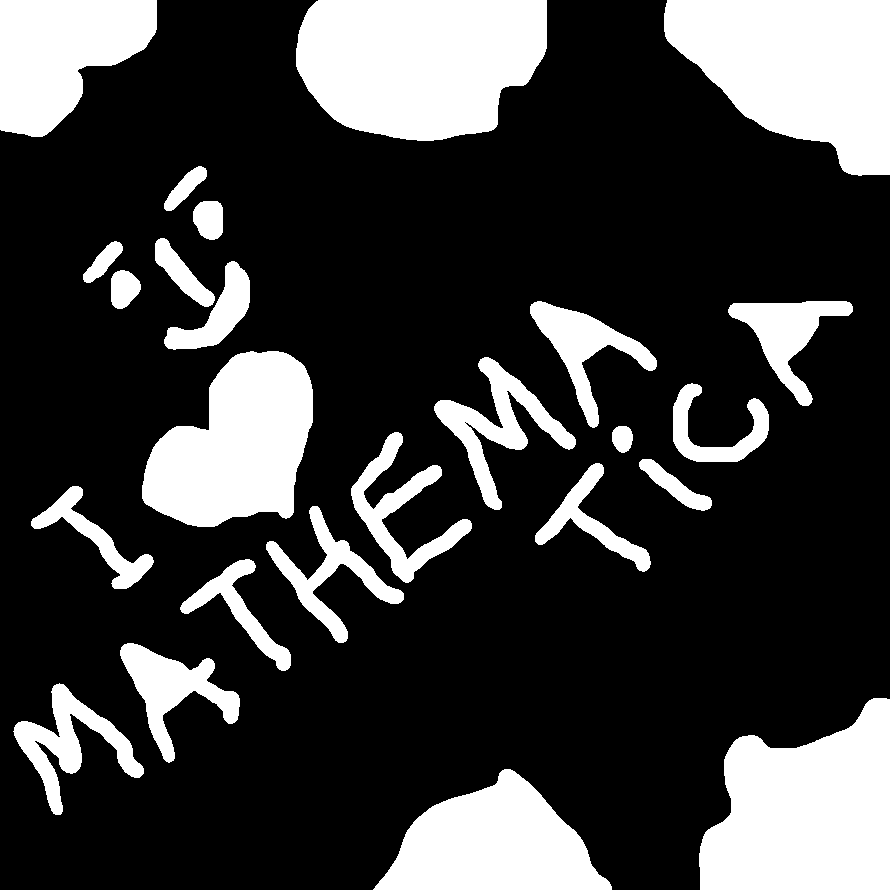
Notice that this definition of "holes connected to borders" is not a well defined concept. An image could very well be a diagonal set of black and white stripes going from top-right to bottom-left and using this technique all black stripes are removed. I am sure you can think of more counter examples.