I submitted the following one-liner entry at the 2017 WTC one-liner competition, and I'd be meaning to ask this question since and kept forgetting:
s = Cases[RulePlot@CellularAutomaton[#], Inset[a_, __] -> a, ?] &;
Join[f = Take[s@99, 1], SequencePredict[s /@ Range@98][f, "NextElement" -> 7]]
Essentially, s is a pure function which, when given an integer, returns a list of the 8 graphics objects which visualize the rules for the elementary cellular automaton with that number. This is illustrated below:
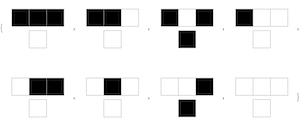
RulePlot[CellularAutomaton[30]]
GraphicsRow[s[30], Frame -> All]
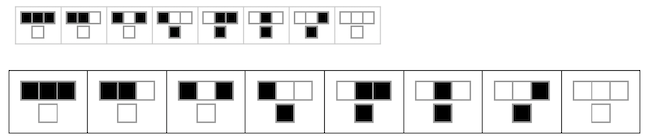
A list of these is generated for the first 98 CAs (in theory skipping 0, but oh well we had to save characters), and passed into SequencePredict which uses a Markov Model to return a SequencePredictorFunction. Here's how 5 of those sequences look like:
GraphicsGrid[s /@ Range[5]]

This is where things get interesting: given only the first rule image of the 99th CA, the predictor correctly 'guesses' the next 7 elements, returning the RulePlot for CA 99!
Looking at the image above, it's clear that the CAs were listed using some sort of loop, which is likely what the predictor picks up. However the result was odd enough (since inherently the ruleplot is not really a sequence) to trigger my curiosity and I was wondering if anyone had a clearer explanation as to what is happening allowing it to predict correctly one element at a time.
Cheers,
George