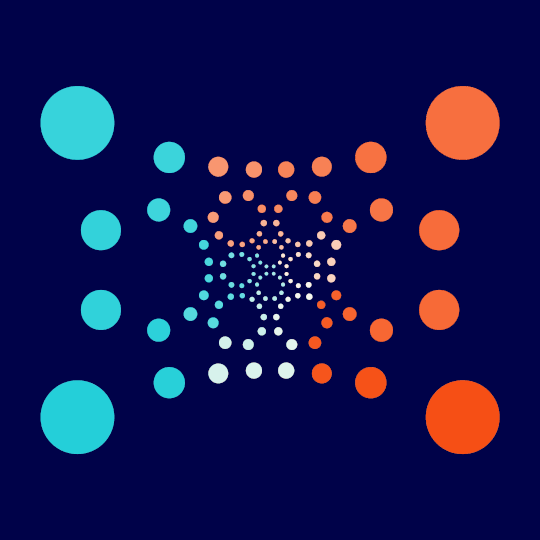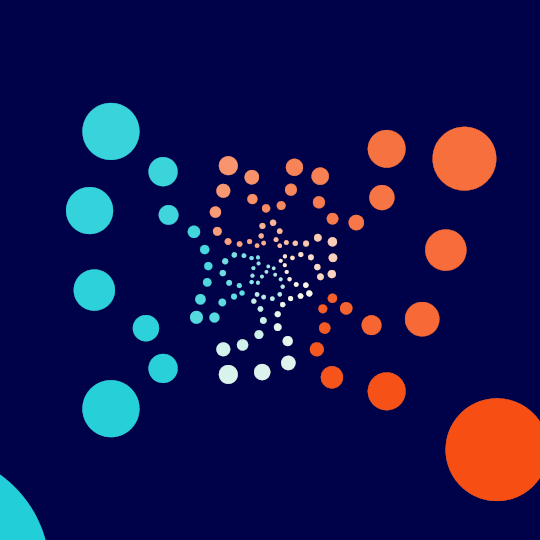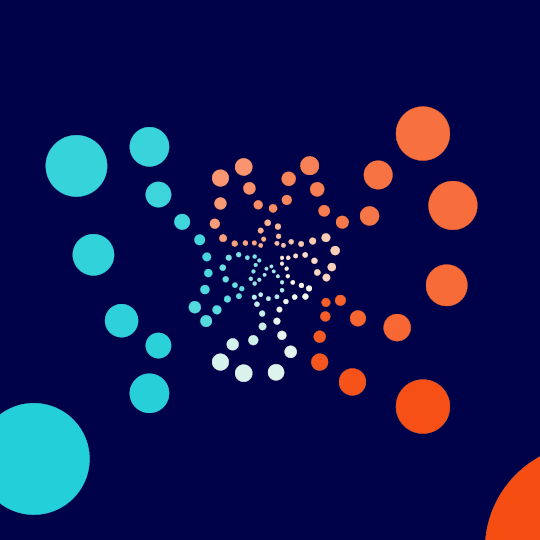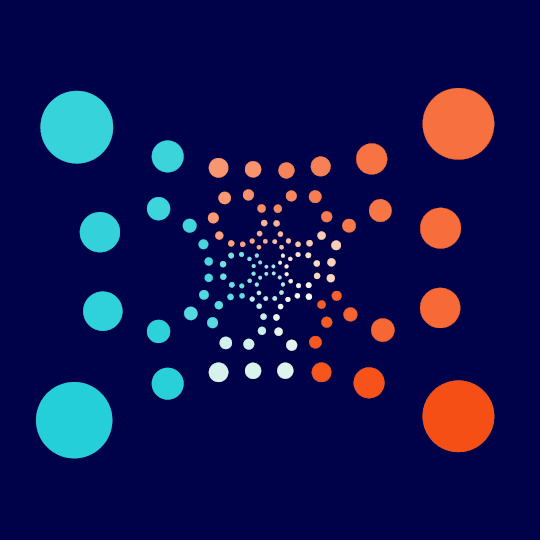
Small Changes
This is the same idea as what I've been doing recently with Touch Em All, All Day, How Does That Work?, and Throw, but one dimension down: find a Hamiltonian cycle on the 1-skeleton of the great rhombicosidodecahedron, normalize to get everything happening on the unit sphere, then stereographically project down to the plane.
First of all, we can extract the vertex coordinates from PolyhedronData[], find a Hamiltonian cycle using FindHamiltonianCycle[], and then re-order the vertices to be in the order they appear in the cycle:
sortedGRVertices =
Module[
{v = N[PolyhedronData["GreatRhombicosidodecahedron", "VertexCoordinates"]],
M, ?, cycle},
? = PolyhedronData["GreatRhombicosidodecahedron", "SkeletonGraph"];
cycle = FindHamiltonianCycle[?];
v[[#[[1]] & /@ (cycle[[1]] /. UndirectedEdge -> List)]]
];
Now, I'm going to form spherical circles of radius $1/4$ the spherical distance between adjacent vertices and then stereographically project them down to the plane. Stereographic projection takes circles to circles, but unfortunately the stereographic image of the center is not the center of the stereographic image of the circle, which makes things complicated. Nonetheless, the function ProjectedSphericalCircle[] (defined below) inputs the center and radius of the circle up in the sphere and outputs a Disk[] object with the correct center and radius.
With that in hand, then, here's the code for an interactive version of the above animation:
DynamicModule[{r, ?, n, pts = Normalize /@ sortedGRVertices,
cols = RGBColor /@ {"#1DCED8", "#FAF9F0", "#F6490D", "#000249"}},
r = Min[DeleteCases[Flatten@Outer[VectorAngle, pts, pts, 1], 0.]];
n = Length[pts];
Manipulate[
? = r unsmoothstep[t];
Graphics[
Table[
{Blend[cols[[;; -2]], Mod[i + 27 + t, n, 1]/(n - 1)],
ProjectedSphericalCircle[
RotationMatrix[-?/2, {0, 0, 1}].
RotationMatrix[?, {pts[[i]], pts[[Mod[i + 1, Length[pts], 1]]]}].
pts[[i]],
r/4]},
{i, 1, Length[pts]}],
PlotRange -> 5, ImageSize -> 540, Background -> cols[[-1]]],
{t, 0, 1}]
]
Finally, then, is the definition of ProjectedSphericalCircle[], which is quite ugly. I don't want to say too much about where it came from, other than that it was essentially the same procedure is described in the post on Inside: stereographically project an arbitrary circle on the sphere down to the plane and solve for the point where the normals to two distinct points intersect to find the center, and then of course the distance from either of those points to the center is the radius. Here's the definition:
ProjectedSphericalCircle[{x_, y_, z_}, r_] :=
If[Chop[x] == Chop[y] == 0. && Chop[z + 1] == 0,
Disk[{0, 0}, Tan[r/2]],
Disk[{(x Cos[r] + (x z Sin[r])/Sqrt[1 - z^2])/(
1 - z Cos[r] - ((-x^2 - y^2) Sin[r])/Sqrt[
1 - z^2]) + (Sqrt[2]
Sin[r] (x Sqrt[1 - z^2] (-1 + z Cos[r]) +
x (-1 + z^2) Sin[r]) ((
x Cos[r] - (y Sin[r])/Sqrt[1 - z^2])/(1 - z Cos[r]) - (
x Cos[r] + (x z Sin[r])/Sqrt[1 - z^2])/(
1 - z Cos[r] - ((-x^2 - y^2) Sin[r])/Sqrt[
1 - z^2])))/((-Sqrt[1 - z^2] +
z Sqrt[1 - z^2]
Cos[r] + (-1 + z^2) Sin[
r])^2 ?(((-1 + z^2)^2 Sin[
r]^2 (3 - 4 z Cos[r] - Cos[2 r] + 2 z^2 Cos[2 r] +
4 Sqrt[1 - z^2] Sin[r] -
2 z Sqrt[1 - z^2] Sin[2 r]))/(-Sqrt[1 - z^2] +
z Sqrt[1 - z^2]
Cos[r] + (-1 + z^2) Sin[r])^4) (-((2 Sqrt[2]
Sin[r] (y Sqrt[1 - z^2] (z - Cos[r]) +
x (-1 + z^2) Sin[r]))/((-Sqrt[1 - z^2] +
z Sqrt[1 - z^2]
Cos[r])^2 ?(1/(-1 + z Cos[r])^4 (8 + 4 z^2 -
16 z Cos[r] - Cos[2 r] + 5 z^2 Cos[2 r] -
Cos[2 (?/2 + r)] +
z^2 Cos[2 (?/2 + r)]) Sin[r]^2))) + (Sqrt[2]
Sin[r] (x Sqrt[1 - z^2] (-1 + z Cos[r]) +
x (-1 + z^2) Sin[r]))/((-Sqrt[1 - z^2] +
z Sqrt[1 - z^2]
Cos[r] + (-1 + z^2) Sin[
r])^2 ?(((-1 + z^2)^2 Sin[
r]^2 (3 - 4 z Cos[r] - Cos[2 r] + 2 z^2 Cos[2 r] +
4 Sqrt[1 - z^2] Sin[r] -
2 z Sqrt[1 - z^2] Sin[2 r]))/(-Sqrt[1 - z^2] +
z Sqrt[1 - z^2] Cos[r] + (-1 + z^2) Sin[r])^4)))), (
y Cos[r] + (y z Sin[r])/Sqrt[1 - z^2])/(
1 - z Cos[r] - ((-x^2 - y^2) Sin[r])/Sqrt[
1 - z^2]) + (2 Sqrt[2]
Sin[r] (y Sqrt[1 - z^2] (-1 + z Cos[r]) +
y (-1 + z^2) Sin[r]) ((
x Cos[r] - (y Sin[r])/Sqrt[1 - z^2])/(1 - z Cos[r]) - (
x Cos[r] + (x z Sin[r])/Sqrt[1 - z^2])/(
1 - z Cos[r] - ((-x^2 - y^2) Sin[r])/Sqrt[
1 - z^2])))/((-Sqrt[1 - z^2] +
z Sqrt[1 - z^2]
Cos[r] + (-1 + z^2) Sin[
r])^2 ?(((-1 + z^2)^2 Sin[
r]^2 (12 - 16 z Cos[r] - 2 Cos[2 r] +
2 z^2 Cos[2 r] + (-2 + 6 z^2) Cos[2 r] +
16 Sqrt[1 - z^2] Sin[r] -
8 z Sqrt[1 - z^2] Sin[2 r]))/(-Sqrt[1 - z^2] +
z Sqrt[1 - z^2]
Cos[r] + (-1 + z^2) Sin[r])^4) (-((2 Sqrt[2]
Sin[r] (y Sqrt[1 - z^2] (z - Cos[r]) +
x (-1 + z^2) Sin[r]))/((-Sqrt[1 - z^2] +
z Sqrt[1 - z^2]
Cos[r])^2 ?(((-1 + z^2)^2 (8 - 16 z Cos[r] +
Cos[2 r] + (-2 + 6 z^2) Cos[2 r] -
Cos[2 (?/2 + r)] +
z^2 (4 - Cos[2 r] + Cos[2 (?/2 + r)])) Sin[
r]^2)/(-Sqrt[1 - z^2] +
z Sqrt[1 - z^2] Cos[r])^4))) + (2 Sqrt[2]
Sin[r] (x Sqrt[1 - z^2] (-1 + z Cos[r]) +
x (-1 + z^2) Sin[r]))/((-Sqrt[1 - z^2] +
z Sqrt[1 - z^2]
Cos[r] + (-1 + z^2) Sin[
r])^2 ?(((-1 + z^2)^2 Sin[
r]^2 (12 - 16 z Cos[r] - 2 Cos[2 r] +
2 z^2 Cos[2 r] + (-2 + 6 z^2) Cos[2 r] +
16 Sqrt[1 - z^2] Sin[r] -
8 z Sqrt[1 - z^2] Sin[2 r]))/(-Sqrt[1 - z^2] +
z Sqrt[1 - z^2] Cos[r] + (-1 + z^2) Sin[r])^4))))},
Abs[((x Cos[r] - (y Sin[r])/Sqrt[1 - z^2])/(1 - z Cos[r]) - (
x Cos[r] + (x z Sin[r])/Sqrt[1 - z^2])/(
1 - z Cos[r] - ((-x^2 - y^2) Sin[r])/Sqrt[
1 - z^2]))/(-((2 Sqrt[2]
Sin[r] (y Sqrt[1 - z^2] (z - Cos[r]) +
x (-1 + z^2) Sin[r]))/((-Sqrt[1 - z^2] +
z Sqrt[1 - z^2]
Cos[r])^2 ?(((-1 + z^2)^2 (8 - 16 z Cos[r] +
Cos[2 r] + (-2 + 6 z^2) Cos[2 r] -
Cos[2 (?/2 + r)] +
z^2 (4 - Cos[2 r] + Cos[2 (?/2 + r)])) Sin[
r]^2)/(-Sqrt[1 - z^2] +
z Sqrt[1 - z^2] Cos[r])^4))) + (2 Sqrt[2]
Sin[r] (x Sqrt[1 - z^2] (-1 + z Cos[r]) +
x (-1 + z^2) Sin[r]))/((-Sqrt[1 - z^2] +
z Sqrt[1 - z^2]
Cos[r] + (-1 + z^2) Sin[
r])^2 ?(((-1 + z^2)^2 Sin[
r]^2 (12 - 16 z Cos[r] - 2 Cos[2 r] +
2 z^2 Cos[2 r] + (-2 + 6 z^2) Cos[2 r] +
16 Sqrt[1 - z^2] Sin[r] -
8 z Sqrt[1 - z^2] Sin[2 r]))/(-Sqrt[1 - z^2] +
z Sqrt[1 - z^2] Cos[r] + (-1 + z^2) Sin[r])^4)))]]]