Because Mathematica does not have this function (yet) I give here a simple way to produce a cobweb plot:
http://en.wikipedia.org/wiki/Cobweb_plotThe code is quite short and does the basics:
ClearAll[CobwebPlot]
Options[CobwebPlot]=Join[{CobStyle->Automatic},Options[Graphics]];
CobwebPlot[f_,start_?NumericQ,n_,xrange:{xmin_,xmax_},opts:OptionsPattern[]]:=Module[{cob,x,g1,coor},
cob=NestList[f,N[start],n];
coor = Partition[Riffle[cob,cob],2,1];
coor[[1,2]]=0;
cobstyle=OptionValue[CobwebPlot,CobStyle];
cobstyle=If[cobstyle===Automatic,Red,cobstyle];
g1=Graphics[{cobstyle,Line[coor]}];
Show[{Plot[{x,f[x]},{x,xmin,xmax},PlotStyle->{{Thick,Black},Black}],g1},FilterRules[{opts},Options[Graphics]]]
]
The function works as follows:
CobwebPlot[f,start,n,xrange,...]
Where
f is a pure function
start is the starting value
n is number of iterations
xrange is a the range of the plot and should have the form: {xminimum,xmaximum}.
The color of the cobweb can be given by a CobStyle option, additionally one can add other options as well (those of Graphics).
Examples:
CobwebPlot[Sqrt[3#-1]&,1,40,{0,4},PlotRange->{{0,3.5},{0,3}},Frame->True,Axes->False,CobStyle->Directive[Dashed,Red],PlotRangePadding->None]
CobwebPlot[0.77#(5-#)&,0.3,30,{0,10},PlotRange->{{0,6},{0,7}},Frame->True,Axes->False,CobStyle->Directive[Blue,Thick],PlotRangePadding->None]
CobwebPlot[10-1.5Abs[#-2]+1.35Sin[5#]&,1.5,230,{-5,12},PlotRange->{Automatic,{-5,12}},Frame->True,Axes->False,CobStyle->Red,PlotRangePadding->None]
giving:
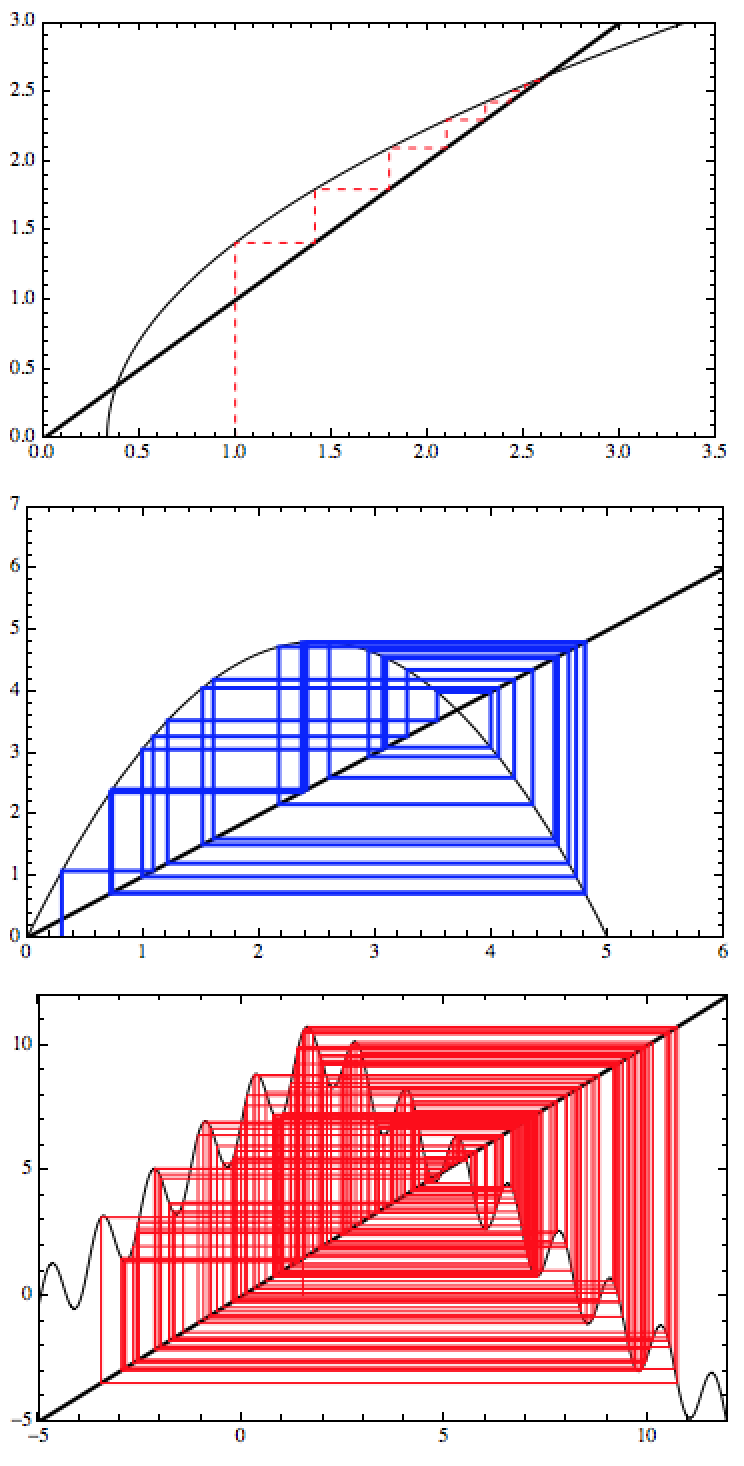
Of course this can be used together with Manipulate like so:
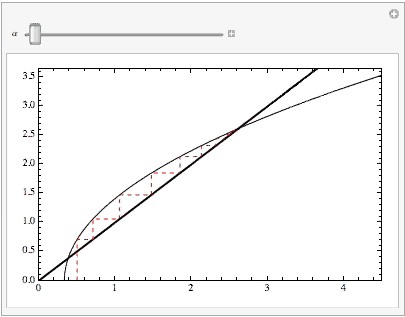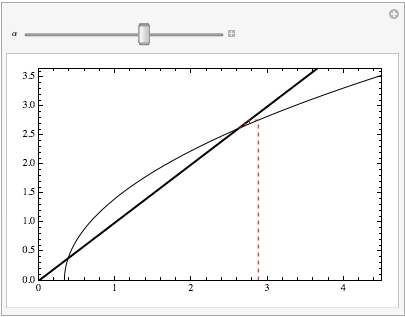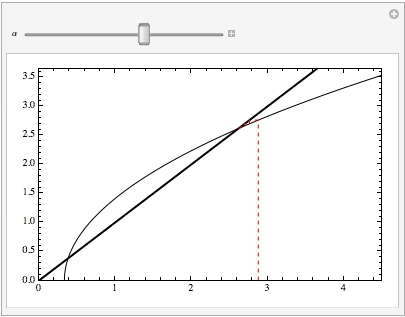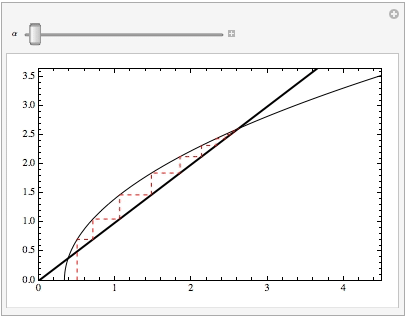
Manipulate[CobwebPlot[Sqrt[3#-1]&,\[Alpha],40,{0,5},PlotRange->{{0,4.5},{0,3.65}},Frame->True,Axes->False,CobStyle->Directive[Dashed,Red],PlotRangePadding->None],{\[Alpha],0.5,4.375}]
giving:
I hope this will be useful. Let me know if you can't get it to work.