Open in Cloud | Download to Desktop via Attachments Below

I recently got inspired by a sculpture sold on Saatchi Art featuring anamorphic deformation by reflection in a spherical mirror. Being curious and interested in anamorphic transformations, I wanted to build something similar and find the math behind it using Mathematica...

A plain, undecorated Christmas ball can serve as a perfect convex spherical mirror to test some of our physics and coding skills. I used a 7 cm XMas ball now dumped in stores for Euro1.75 a sixpack! In a nutshell: I wanted to see how a deformed text should look like in order to show up undeformed when reflected in a ball shaped mirror. 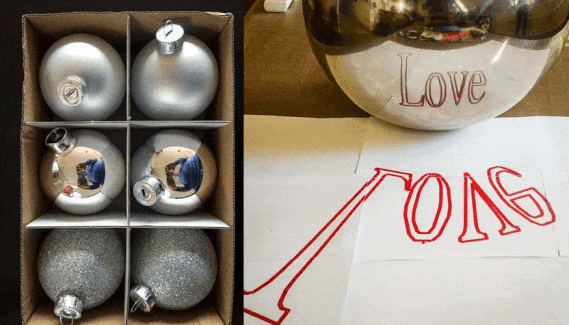
The graphics below show a spherical mirror centered at C:(0,0,0), our eye at viewpoint V: (xv,0,zv) and a reflected point S on the base plane beneath the ball. One of the reflected light rays leaving S will meet the mirror at Q such that its reflection meets the eye at V. But the eye at V will now perceive the point S at I. 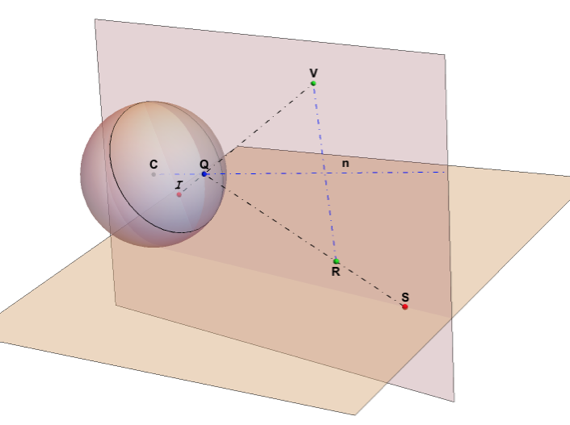
I is a perceived image point inside the view disk perpendicular to VC. According to the law of reflection, the lines VQI and SRQ will form equal angles with the normal n to the sphere in Q. All image points will be restricted to a disk that is the base of the view cone with the line CV as axis and an opening angle of tan^-1(zv/xv). This image disk is at an offset 1/xv from C and has a radius of Sqrt[1-(1/xv)^2]. 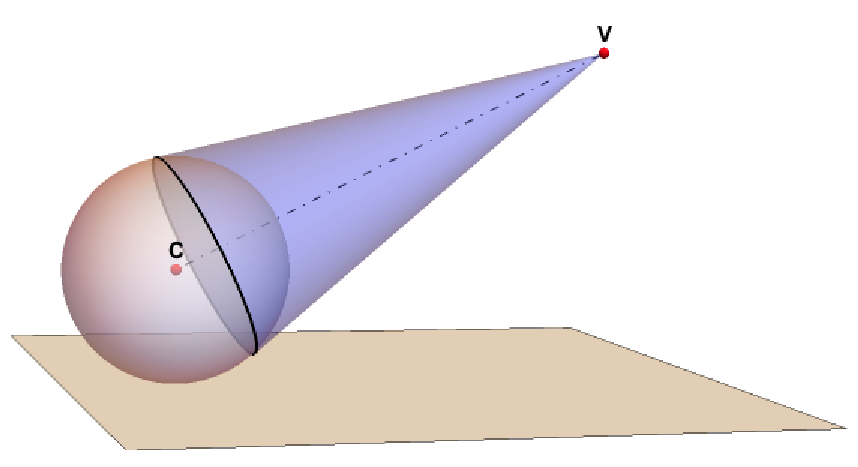
The point Q (q1, q2, q3) is the intersection of the view line VI and the mirror sphere. It can be computed by solving this equation:
solQ = NSolve[
Element[{x, y, z}, HalfLine[{imagePointI, viewPointV}]] &&
Element[{x, y, z}, Sphere[]], {x, y, z}];
pointQ = First[{x, y, z} /. solQ]; {q1, q2, q3} = pointQ;
The points C, Q, I, V and S are all in the same plane. We have R, the projection of V to the normal n.
projectionPlane = InfinitePlane[pointQ, {pointQ, viewPointV}];
reflectionPt = 2 Projection[viewPointV, pointQ] - viewPointV;
The point S is now the intersection of of the line QR with the base plane. It can be computed by solving this equation:
solS = NSolve[{{x, y, z} \[Element]
HalfLine[{{q1, q2, q3}, reflectionPt}] && {x, y, z} \[Element]
InfinitePlane[{{0, 0, -1}, {0, 1, -1}, {0, -1, -1}}]}, {x, y,
z}];
After simplification, we can write the following function that maps the perceived image point I to the reflected point R :
xmasBallMap[iPt : {yi_, zi_}, vPt : {xv_, zv_}] :=
Module[{imagePtRotated, solQ, q1, q2, q3},
(*image point in real (rotated) pane*)
imagePtRotated = {(1 - zi zv)/Norm@vPt,
yi, (xv^2 zi + zv)/xv/Norm@vPt};
(*intersection viewline-sphere: Q*)
solQ = NSolve[
Element[{x, y, z}, HalfLine[{imagePtRotated, {xv, 0, zv}}]] &&
Element[{x, y, z}, Sphere[]], {x, y, z}];
{q1, q2, q3} = First[{x, y, z} /. solQ];
Join[{-(1 + q3) (q2^2 + q3^2) xv + q1^2 (xv - q3 xv) +
q1^3 (-1 + zv) + q1 q2^2 (-1 + zv) +
q1 q3 (q3 (-1 + zv) + 2 zv),
q2 (2 q1 xv + q1^2 (-1 + zv) + q2^2 (-1 + zv) +
q3 (q3 (-1 + zv) + 2 zv))}/(-2 q1 q3 xv + q3^2 (q3 - zv) +
q1^2 (q3 + zv) + q2^2 (q3 + zv)), {-1}]]
All possible image points have to fit inside the lower half-disk. This is a grid of image points inside the view disk:
pts = Table[
Table[{x, y}, {x, -Floor[Sqrt[1 - y^2], .1] + .1,
Floor[Sqrt[1 - y^2], .1] - .1, .025}], {y, 0, -.9, -.025}];
viewDisk = Graphics[{Circle[{0, 0}, 1, {\[Pi], 2. \[Pi]}],
{AbsolutePointSize[2], Point /@ pts}}, Axes -> True,
AxesOrigin -> {-1, -1}, AxesStyle -> Directive[Thin, Red]]
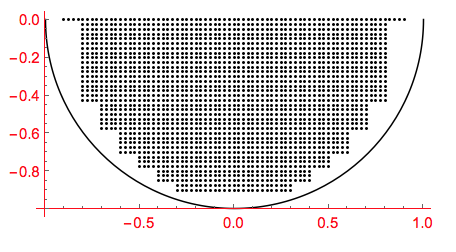
This is the reflected spherical anamorphic map of these points:
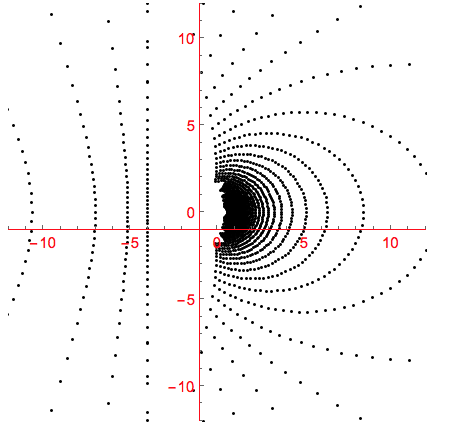
We can see that there is a large magnification between the perceived image inside the ball and it reflected image. Getting a point too close to the rim of the view disk will project its reflection far away. This GIF shows the function in action. The image point I follows a circle in the perceived image disk while its reflection S follows the closed curve of its map xmasBallmap(I, v) in the base plane. 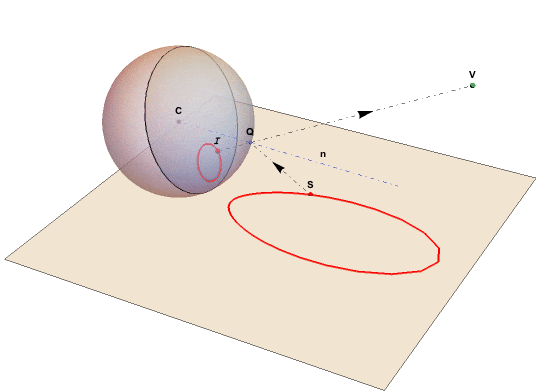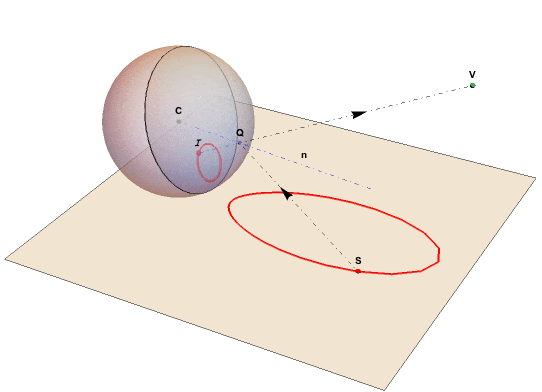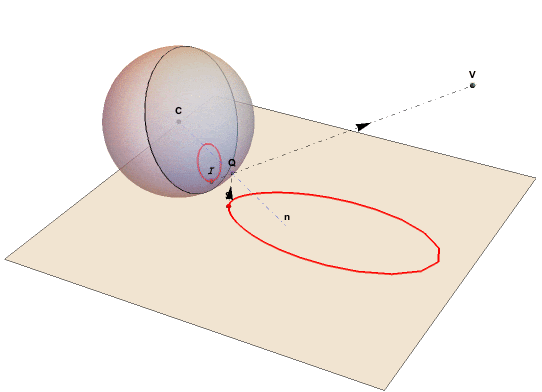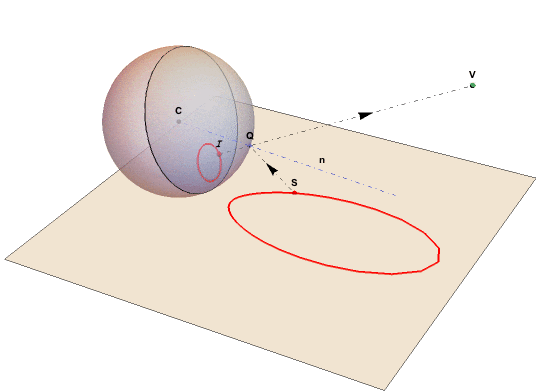
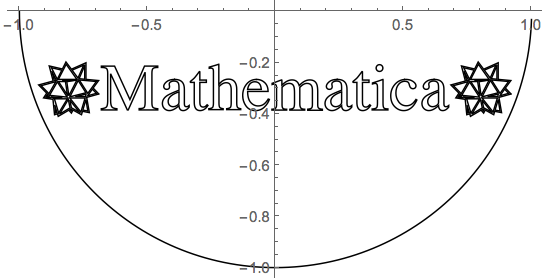
We can now further test our function with some text e.g.: "[MathematicaIcon]Mathematica[MathematicaIcon]".
ma = First[First[
ImportString[
ExportString[
Style["\[MathematicaIcon]Mathematica\[MathematicaIcon]",
FontFamily -> "Times", FontSize -> 72], "PDF"],
"TextMode" -> "Outlines"]]] /. FilledCurve :> JoinedCurve;
The text image needs to be rescaled and centered to fit inside the ball.
maCenteredScaled =
ma /. {x_?NumericQ, y_?NumericQ} :> {x, y}*.005 /. {x_?NumericQ,
y_?NumericQ} :> {x - .93, y - .45};
This shows the text as should be perceived in the lower half of the mirror sphere:
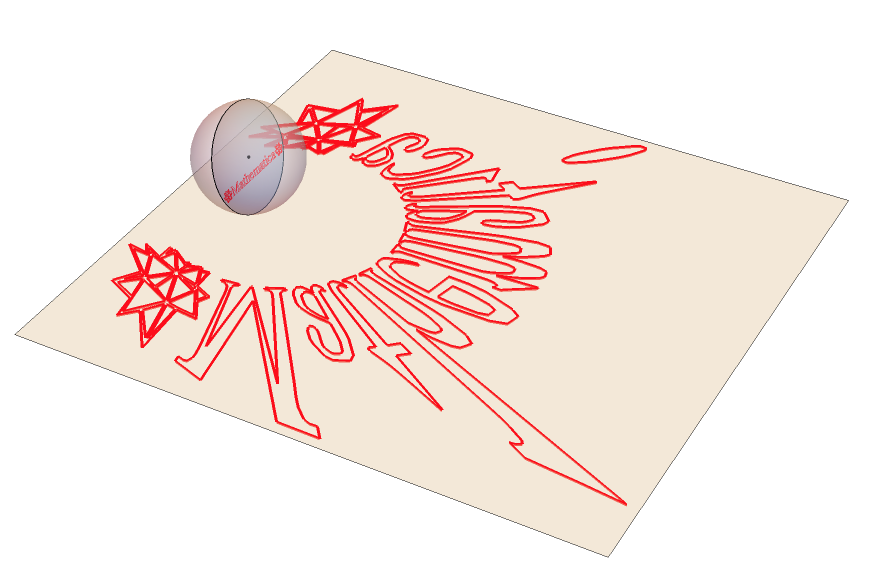
This is the code for a 3D view of the complete setup: the spherical mirror, the perceived text in the disk inside the sphere and the deformed, anamorphic image on the base plane.
Quiet@Module[{xv = 10., zv = 3., \[Phi], rotationTF, pointA, viewPt,
mathPts, rotatedMathPts, reflectedPts},
(*view angle*)\[Phi] = ArcTan[xv, zv];
rotationTF = RotationTransform[-\[Phi], {0, 1, 0}, {0, 0, 0}];
(*view pane rotation anchor*)
pointA = {(0 - .01) Cos[\[Phi]], 0, (0 - .01) Sin[\[Phi]]};
(*point coordinates in y-z plane*)
mathPts = maCenteredScaled[[-1, 1, All, -1]];
rotatedMathPts =
Map[rotationTF,
mathPts /. {y_?NumericQ, z_?NumericQ} :> {0, y, z}, {3}];
reflectedPts = Map[xmasBallMap[#, {xv, zv}] &, mathPts, {3}];
Graphics3D[{
(*reflected image plane (floor)*){Opacity[.45], LightBlue,
InfinitePlane[{{0, 0, -1}, {1, 0, -1}, {-1, .5, -1}}]},
(*mirror sphere*){Opacity[.35], Sphere[]},
(*center of sphere*){Black, Sphere[{0, 0, 0}, .03]},
(*percieved image pane*){Opacity[.35],
Cylinder[{{0, 0, 0}, pointA}, 1]},
(*perceived image*){Red, Line /@ rotatedMathPts},
(*reflected image*){Red, AbsoluteThickness[3],
Line /@ reflectedPts}},
Boxed -> False]]
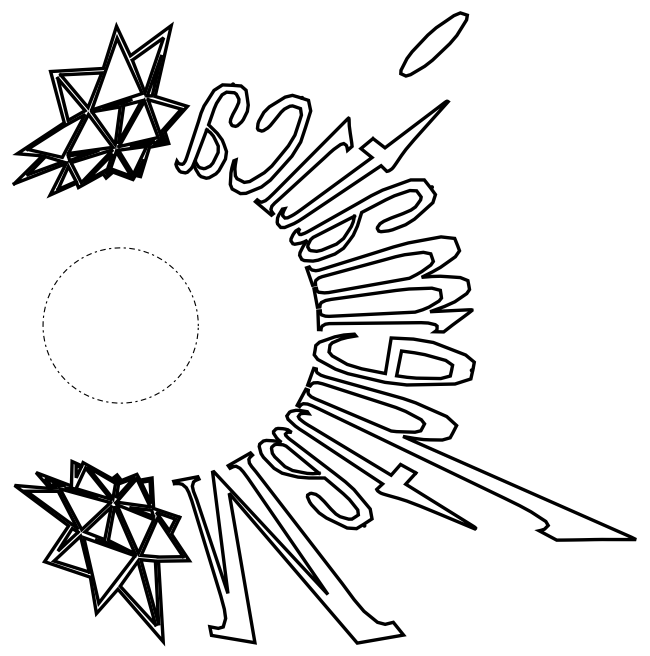
Time to try the real thing. This shows a 7cm diameter XMas ball mirror with the text reflected in it. 
Get yourself a nice reflecting Christmas ball and this is a pdf for you to printout and try it! (see attached pdf file for printing)
 Attachments:
Attachments: