Open in Cloud | Attachments for Desktop at the End | LARGE images, wait till they load

And so, the holidays are upon us once more and celebrations are in order. Wolfram Language fans enjoy fun recreation and arts, because beautiful things can be made with beautiful code, concise and elegant. I wanted to find a few gems from the past to honor the holidays and the traditions our users have. Surprisingly those few gems combined into one Christmas postcard you can see above.

The story of this postcard begins six years ago, when our sister community Mathematica Stack Exchange sprang up a question about simulating a snow fall with Wolfram Language. One of Wolfram most creative users, @Simon Woods gave a wonderful answer that was very popular. Then about five years ago I have run into a viral Reddit discussion dubbed

$$t * sin (t) ? Christmas tree$$

which showcased a beautiful minimalistic Christmas tree built with simple $t * sin (t)$ function and Java Script. I recreated the concept with Wolfram Language and our another wonderful user @Silvia Hao ornamented it with festoon lamps. An idea came to me to combine them, because a Christmas Tree sparkling lights in a snowfall is the icon of winter holidays. But beware a few subtle tricks ;-) In depth those discussed at the original references I gave. Below are slightly changed code and a few comments.

The Tree

Our Christmas Tree is indeed spun with $t * sin (t)$. But in 3D rather than 2D. This is basically a conical spiral whose amplitude increases, a 2D circle dragged along 3-rd axis like this:

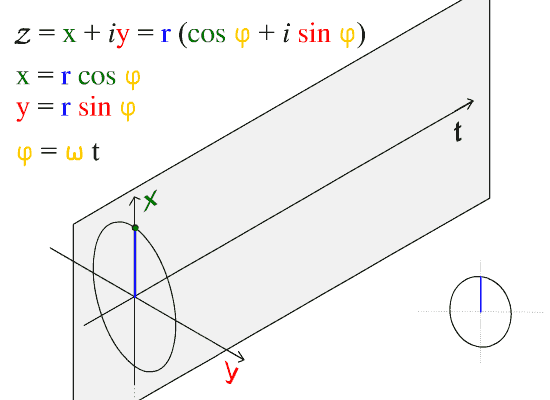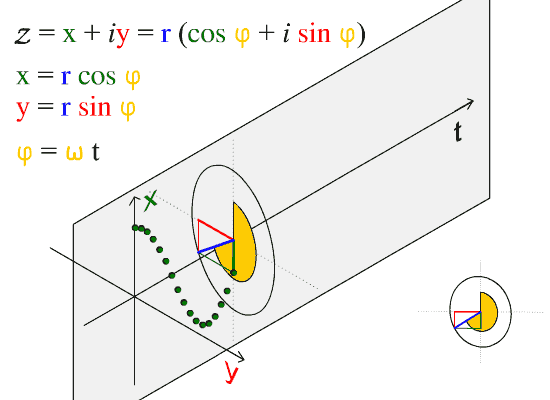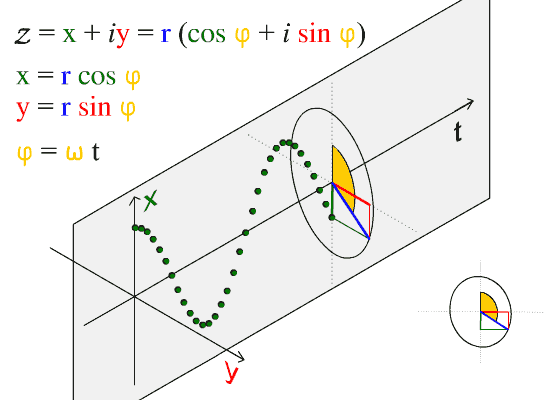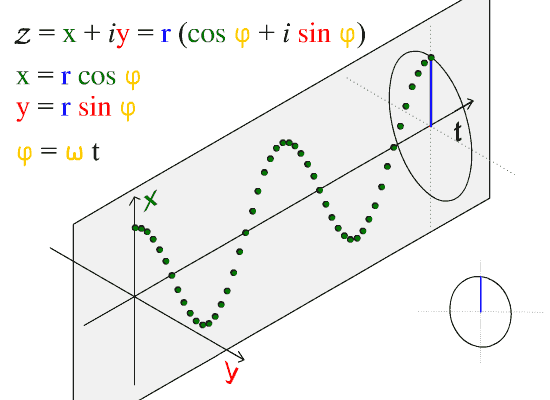
but only with increasing radius. Density of lights and their motion is one subtlety to take care of with math. Another subtlety is increasing 3D depth perception by slightly dimming the lights that are further from the observer. This function defines the mathematics of the tree:

 PD = .5;
 s[t_, f_] := t^.6 - f
 dt[cl_, ps_, sg_, hf_, dp_, f_, flag_] :=
  Module[{sv, basePt},
         {PointSize[ps],
          sv = s[t, f];
          Hue[cl (1 + Sin[.02 t])/2, 1, .8 + sg .2 Sin[hf sv]],
          basePt = {-sg s[t, f] Sin[sv], -sg s[t, f] Cos[sv], dp + sv};
          Point[basePt],
         If[flag,
            {Hue[cl (1 + Sin[.1 t])/2, 1, .8 + sg .2 Sin[hf sv]], PointSize[RandomReal[.01]],
             Point[basePt + 1/2 RotationTransform[20 sv, {-Cos[sv], Sin[sv], 0}][{Sin[sv], Cos[sv], 0}]]},
            {}]
        }]

and this code uses the function to build 228 frames of the animated tree:

treeFrames = ParallelTable[
                       Graphics3D[Table[{
                                         dt[1, .01, -1, 1, 0, f, True], 
                                         dt[.45, .01, 1, 1, 0, f, True],
                                         dt[1, .005, -1, 4, .2, f, False], 
                                         dt[.45, .005, 1, 4, .2, f, False]},
                                        {t, 0, 200, PD}],
                                  ViewPoint -> Left, BoxRatios -> {1, 1, 1.3}, 
                                  ViewVertical -> {0, 0, -1}, Boxed -> False,
                                  ViewCenter -> {{0.5, 0.5, 0.5}, {0.5, 0.55}},
                                  PlotRange -> {{-20, 20}, {-20, 20}, {0, 20}}, 
                                  Background -> Black,ImageSize->350],
                       {f, 0, 1, .0044}];

Let's check a single frame of THe Tree:

First[treeFrames]

The Snow

This function below builds a single random snowflake. They are of course six-fold symmetric polygons.

flake := Module[{arm},
   arm = Accumulate[{{0, 0.1}}~Join~RandomReal[{-1, 1}, {5, 2}]];
   arm = arm.Transpose@RotationMatrix[{arm[[-1]], {0, 1}}];
   arm = arm~Join~Rest@Reverse[arm.{{-1, 0}, {0, 1}}];
   Polygon[Flatten[arm.RotationMatrix[# \[Pi]/3] & /@ Range[6], 1]]];

Let's see a few random shapes, they are fun in black on white ;-)

Multicolumn[Table[Graphics[flake, ImageSize -> 50], 100], 10]

Now it's time to build the snowfield which has a few tricks. To simulate 3D perception 2 things need to be obsereved:

1. Real further snowflakes appear smaller

2. Real further snowflakes have slower perceived angular speeds

The 2nd observation is taken care of by the size_ variable below.

snowfield[flakesize_, size_, num_] := 
  Module[{x = 100/flakesize}, 
   ImageData@
    Image[Graphics[{White,Opacity[.8],
       Table[Translate[
         Rotate[flake, RandomReal[{0, \[Pi]/6}]], {RandomReal[{0, x}],
           RandomReal[{0, x}]}], {num}]}, Background -> Black, 
      PlotRange -> {{0, x}, {0, x}}], ImageSize -> {size, size}]];

and by 3 different sizes given here:

size=455;
r=snowfield@@@{{.9,size,250},{1.2,size,30},{1.6,size,10}};

So we sort of have 3 different fields of vision reproaching the observer. The 1st observation is simulated with different speed with which different fields of vision are rotated, the closer one being the fastest. This simulates rotation of the fields of vision and builds the frames for the snowfall:

snowFrames=ParallelTable[Image[Total[(RotateRight[r[[#]],k #]&/@{1,2,3})[[All, ;;size]]]],{k,0,455,2}];

The Postcard

Slight opacity is needed to to blend The Tree and The Snow appealingly. The opacity is given the snowflakes in the code above and SetAlphaChannel below is formally needed for image data to have the same dimensions (3 RGB + 1 Opacity channels) and to be able to combine. This builds the final frames

finalFrames=
Parallelize[MapThread[
    ImageAdd[SetAlphaChannel[#1,1],#2]&,
{treeFrames,snowFrames}]];

and this exports the frames to the GIF you see at the top of the post:

Export["xmas.gif", finalFrames,"AnimationRepetitions"->Infinity]

I hope you had fun. Feel free to share your own crafts. Happy holidays!

Attachments:

The-Mathy-Arts-o...nb