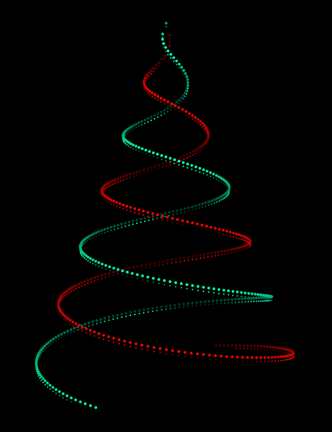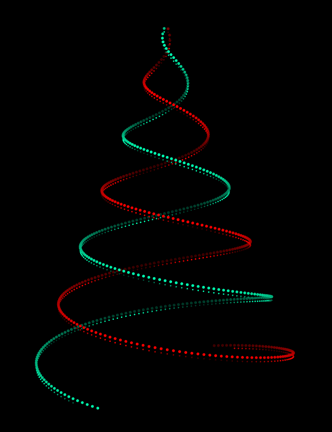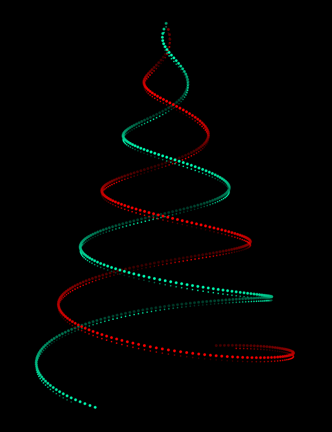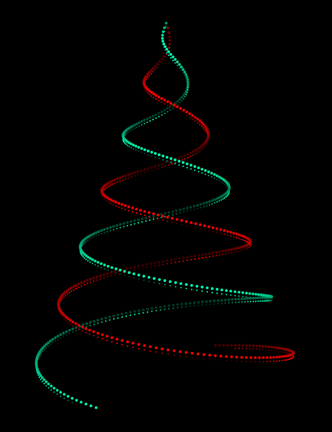
![enter image description here][1]

I noticed that a [2] about programming a lighted Christmas Tree from a simple equation

t*Snt

became very popular on Reddit. It is connected to a [3] a programmer developed. I thought how fast we can make it with Wolfram language ? Here is the result with slight flickering ;-) Note a very special care needs to be paid to the dimming of the lights at a larger distances, and pretty shadowing.

- Function f(t, f) is rescaling sampling rate of driving parameter t of parametric curve so points are distributed uniformly. f is basically phase shift.

- Parameter PD is just average distance between points

This .GIF file has 100 frames. Enjoy! 

PD = .5; s[t_, f_] := t^.6 - f;
dt[cl_, ps_, sg_, hf_, dp_, f_] := {PointSize, Hue[cl, 1, .6 + sg .4 Sin[hf s[t, f]]], 
Point[{-sg s[t, f] Sin[s[t, f]], -sg s[t, f] Cos[s[t, f]], dp + s[t, f]}]};
frames = ParallelTable[
 
Graphics3D[Table[{dt[1, .01, -1, 1, 0, f], dt[.45, .01, 1, 1, 0, f], 
dt[1, .005, -1, 4, .2, f], dt[.45, .005, 1, 4, .2, f]}, {t, 0, 200, PD}],
 
ViewPoint -> Left, BoxRatios -> {1, 1, 1.3}, ViewVertical -> {0, 0, -1}, 
ViewCenter -> {{0.5, 0.5, 0.5}, {0.5, 0.55}}, Boxed -> False, 
PlotRange -> {{-20, 20}, {-20, 20}, {0, 20}}, Background -> Black],
 
{f, 0, 1, .01}];

Export["tree.gif", frames]


[1]: https://community.wolfram.com/c/portal/getImageAttachment?filename=tree.gif&userId=11733
[2]: http://redd.it/1tswai
[3]: https://github.com/anvaka/atree