Message Boards Message Boards

[GIF] Master Control Program (Minimal 7_4 knot on the simple cubic lattice)

Minimal 7_4 knot on the simple cubic lattice

Master Control Program

Continuing the series of minimal lattice knots (1, 2, 3, 4), but now back to the simple cubic lattice with the $7_4$ knot (a.k.a. the endless knot from Buddhism). Here's a more standard view of the $7_4$:

KnotData[{7, 4}, #] & /@ {"Image", "KnotDiagram"}

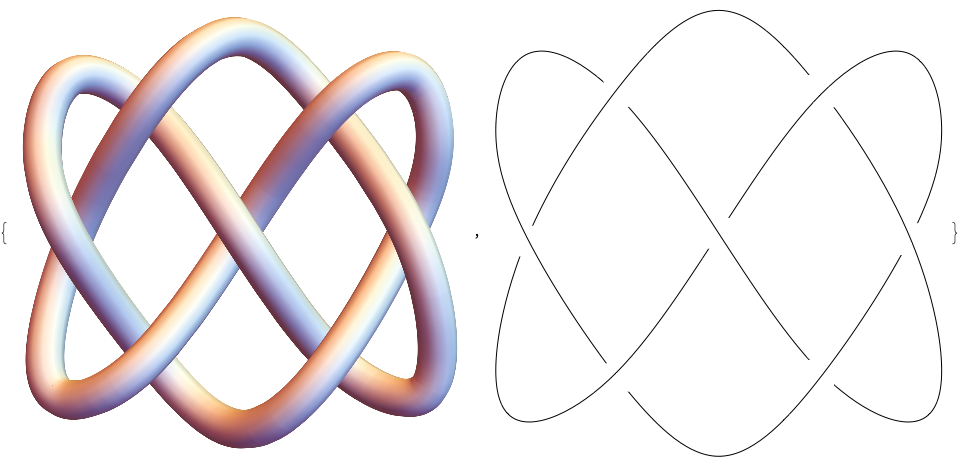
Standard Mathematica views of the 7_4 knot

Once again, we're grabbing the coordinates of this minimal lattice knot from Andrew Rechnitzer's page and mean-centering:

sc74 = Standardize[Import["https://www.math.ubc.ca/~andrewr/knots/data/SC74.dat"], Mean, 1 &];

To get the background gradient I'm using RadialGradientImage, which renders very slowly. If you want a responsive Manipulate, delete the Overlay and the RadialGradientImage, and in the Graphics replace Background -> None with Background -> cols[[-2]].

DynamicModule[{p, q, b, n, θ, pl, 
  cols = RGBColor /@ {"#cdffeb", "#009f9d", "#07456f", "#0f0a3c"}},
 Manipulate[
  θ = ArcCos[-(1/3)] (#^3/(1 - 3 # (1 - #))) &[Mod[t, 1]];
  Which[t < 1 || t == 4,
   {p, q} = Normalize /@ {{1, 1, 1}, {1, 0, -1}};
   {n, b} = {p, q}.RotationMatrix[-θ, {-1, 0, 1}];,
   1 <= t < 2,
   {p, q} = Normalize /@ {{-1, 1, -1}, {1, 0, -1}};
   {n, b} = {p, q}.RotationMatrix[-θ, {0, 1, 1}];,
   2 <= t < 3,
   {p, q} = Normalize /@ {{-1, -1, 1}, {-1, 0, -1}};
   {n, b} = {p, q}.RotationMatrix[- θ, {1, 0, 1}];,
   3 <= t < 4,
   {p, q} = Normalize /@ {{1, -1, -1}, {-1, 0, -1}};
   {n, b} = {p, q}.RotationMatrix[- θ, {0, -1, 1}];
   ];
  pl = sc74.Transpose[{Cross[b, n], b}];
  Overlay[
   {RadialGradientImage[cols[[2 ;;]], {540, 540}],
    Graphics[
     {EdgeForm[
       Directive[Thickness[.025], JoinForm["Round"], cols[[1]]]], 
      FaceForm[None], Polygon[pl]},
     ImageSize -> 540, PlotRange -> 4, Background -> None]}
   ],
  {t, 0, 4}]
 ]
POSTED BY: Clayton Shonkwiler
2 Replies
Sort By:

enter image description here - Congratulations! This post is now a Staff Pick as distinguished by a badge on your profile! Thank you, keep it coming, and consider contributing your work to the The Notebook Archive!

POSTED BY: EDITORIAL BOARD
J. M.
J. M.
Posted 6 years ago

Since the background is a fixed thing and not being actively updated, you can put the initialization in DynamicModule[]; thus, you can do something like

DynamicModule[{p, q, b, n, θ, pl, col = RGBColor["#cdffeb"], 
               bg = RadialGradientImage[RGBColor /@ {"#009f9d", "#07456f", "#0f0a3c"},
                                        {540, 540}]},
Manipulate[(* stuff *)
           Overlay[{bg, Graphics[{EdgeForm[Directive[Thickness[.025],
                                                     JoinForm["Round"], col]],
                                  FaceForm[], Polygon[pl]},
                   ImageSize -> 540, PlotRange -> 4]}], {t, 0, 4}]]

Yet another alternative that avoids Overlay[] would be to use a textured polygon as background. To do that, you can replace the last line inside the Manipulate[] with

Graphics[(* stuff *), ImageSize -> 540, PlotRange -> 4, 
         Prolog -> {Texture[bg], 
                    Polygon[{Scaled[{0, 0}], Scaled[{1, 0}],
                             Scaled[{1, 1}], Scaled[{0, 1}]}, 
                            VertexTextureCoordinates ->
                            {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}]
POSTED BY: J. M.
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract