Introduction

If you were to take a random selection of functions from the Wolfram Language and try compose them in no concerted order to create a program it will most likely result, if it evaluates at all, in:

• $Failed
• a meaningless expression...

But some combinations do give rise to interesting programs. Just take a look at all that has been done with the Wolfram Language. Those programs were made with an intention in mind. A random generator on the other hand can generate any expression including those... Think of this in the perspective of useless and programs and useful programs existing in the same space of all possible combinations of functions.

The goal of this project is to explore this space of possible programs. Let us look for interesting solutions for the toy problem of sequence generation. I experiment bellow on a with a very small subspace of all possible programs.

Selecting my region of the space of possible programs

I decided to restrict myself to functions whose input and output was always of the same type. Those functions are simple to compose together. Lists are easy to work with. There are probably the most used data structure. So I selected a few interesting and simple functions working on and producing lists and grouped them into three classes:

• Atoms = List[1]. These functions are the basic building blocks of the program. Although my project only included one atom, the list of atoms could easily be increased.
• Single argument functions = {Accumulate, Sort, MinMax, Reverse, RotateLeft, RotateRight, ReverseSort, RandomSample}. Some of these would change the elements of the list, while others would rearrange them.
• Two argument functions = {Join, Union, Riffle}. These would consume two lists to produce one list.

I enforced correct composition respecting these groups during generation.

Creation of random programs

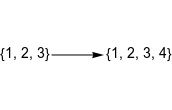
The type of functions used will create programs with a nested structure. To create a random program I start with List[1] and mutate it a number of times. A mutation is created by replacing any function with another. When the number of arguments is increased an atom is used for the missing argument, and all reductions of arguments were prohibited. This is an example of a List[1] being replaced with Riffle. The branches have been rearranged automatically by TreeForm.

Using ReleaseHold we can observe the resulting change in output the program.

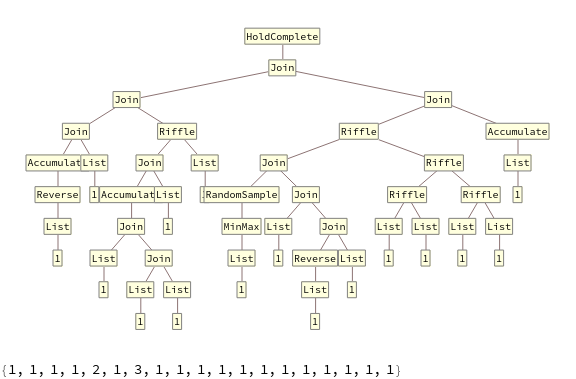
The following program is an example of mutating an atom fifty times, with its output below the expression tree.

Searching for interesting programs

To find interesting programs I used a genetic algorithm, the fitness function depends on how well it produces a sequence of increasing integers. To implement the genetic algorithm I developed the process of crossover, created the fitness function and evolved a population of programs.

Fitness function and selection process

The fitness function was created to favor programs which return a long sequence of ordered successive integers. Tournament selection was used to create the mating pool. This process is done by selecting a random sample of the population, known as a tournament, and sorting them by fitness. From a tournament the best individual is selected with probability p, then the next n individuals are selected each with a probability p*(1-p)^n. Individuals selected go into the mating pool, where crossover and mutation take place to produce the next generation.

Crossover and producing the next generation

During crossover two parent programs are selected. The first parent is used as a body and then a random branch of the body is replaced with a random branch of the second parent. The resulting child is then mutated once and introduced into the new population. This process is repeated until the new population has the same size as the old one.

The results

Good solutions were found relatively quickly, in the 8th generation the best solution created a list of numbers from 1 to 37, with only 6 numbers missing, a lot better than the first generation, which only produced a {1}.

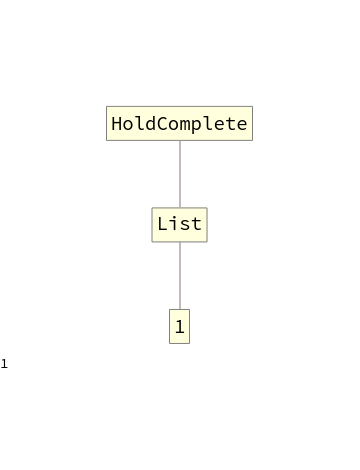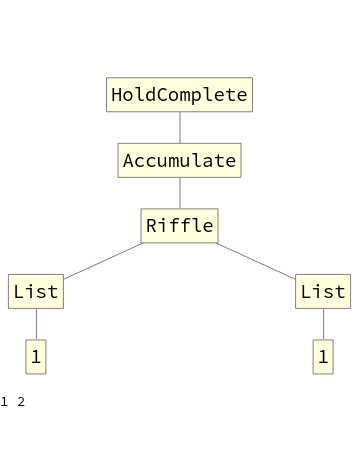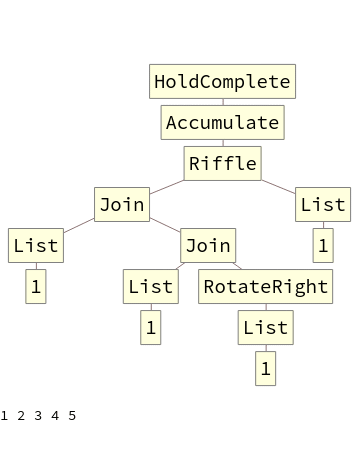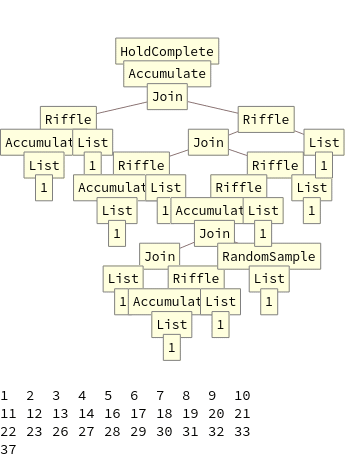
I chose 8 generations because more generations would produce very large programs and the function TreeForm (which I use to display the program) would make a very crowded and hard to understand graph. An example of the best 11th generation program is:

The resulting sequence is almost 68'000 integers long and is very close to the ideal sequence of that length.

What's next?

This project could be extended in many different directions. First, the results of these programs could be studied in more detail, some questions which would be interesting to answer are:

• What patterns do successful programs have? Are they modular?
• Some functions appear to be a lot more common than others, how do they contribute to the fitness of the program?
• What happens with a different set of functions?

Another interesting possibility is to use a different fitness function. The programs could be made to create popular sequences such as:

• Fibonacci sequence
• List of prime numbers
• Digits of pi (or tau if you are a tau fan).
• Random sequences

And of course changing the space of functions to something other than those that work with lists.

The project notebook, along with may drafts can be found in this github repository