Heureka. The solution was discovered thanks to Malthe Andersen who had an inspired solution in this thread: https://community.wolfram.com/groups/-/m/t/1946413

![enter image description here][1]

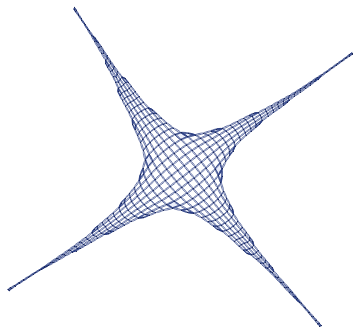
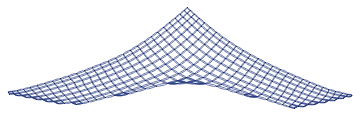
However you still got the problem of long tails.

I found it nicer to pre generate a (partial) pattern using just r1 and then fill is seperatly.

![enter image description here][2]

The current rules:

![enter image description here][3]

![enter image description here][4]

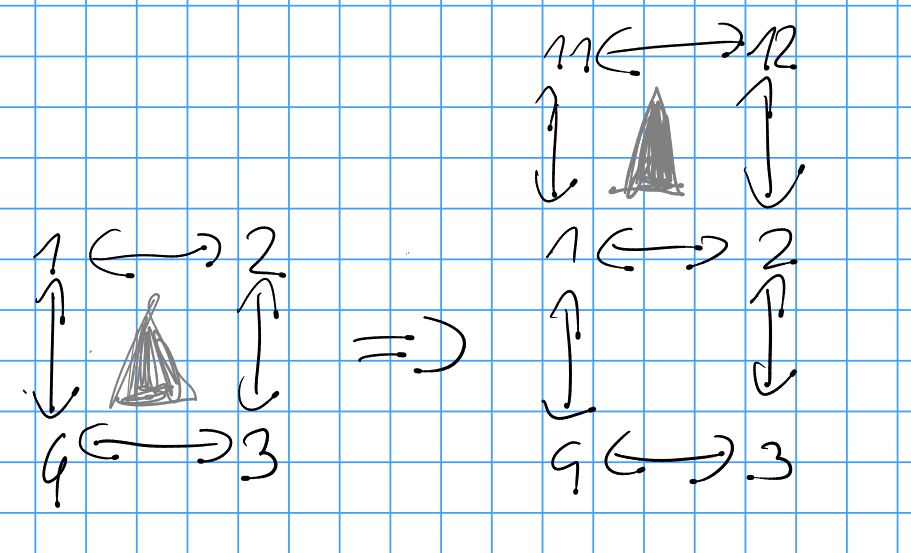
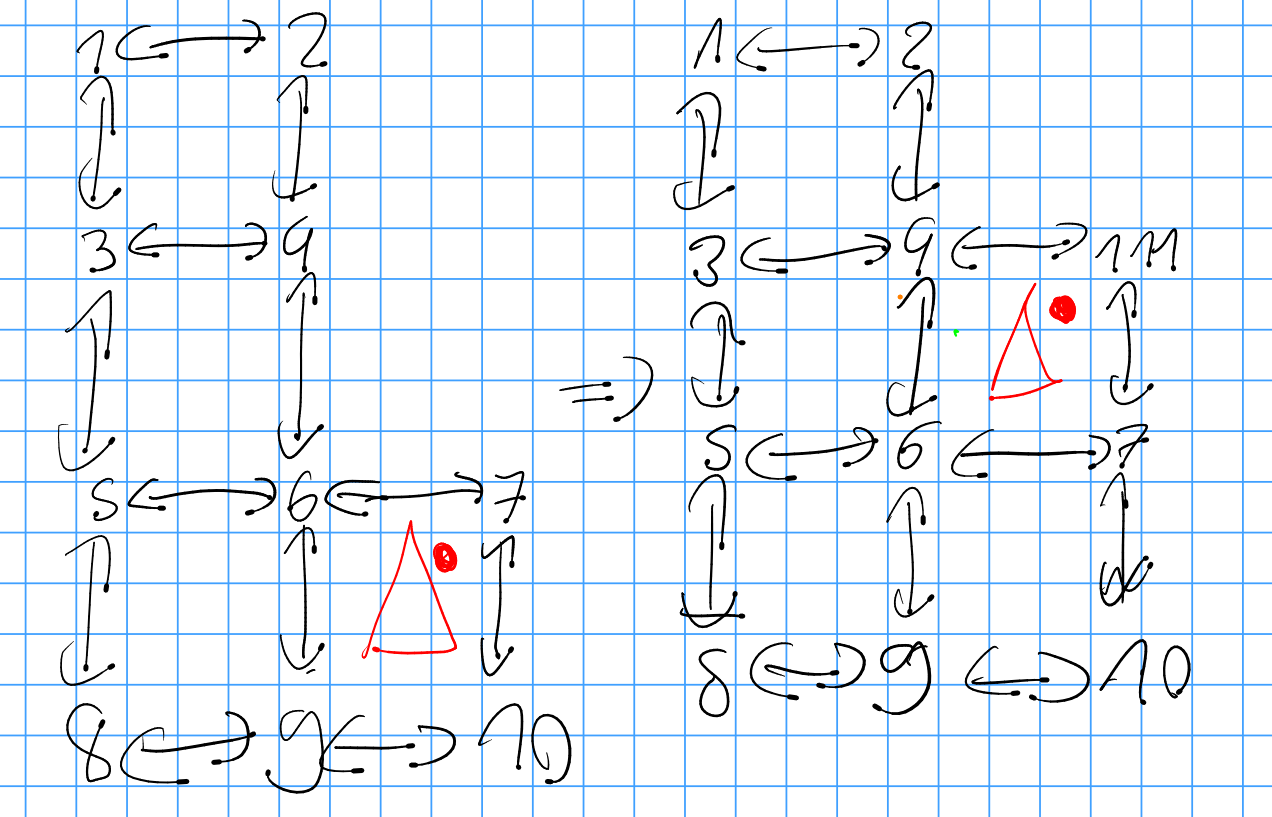
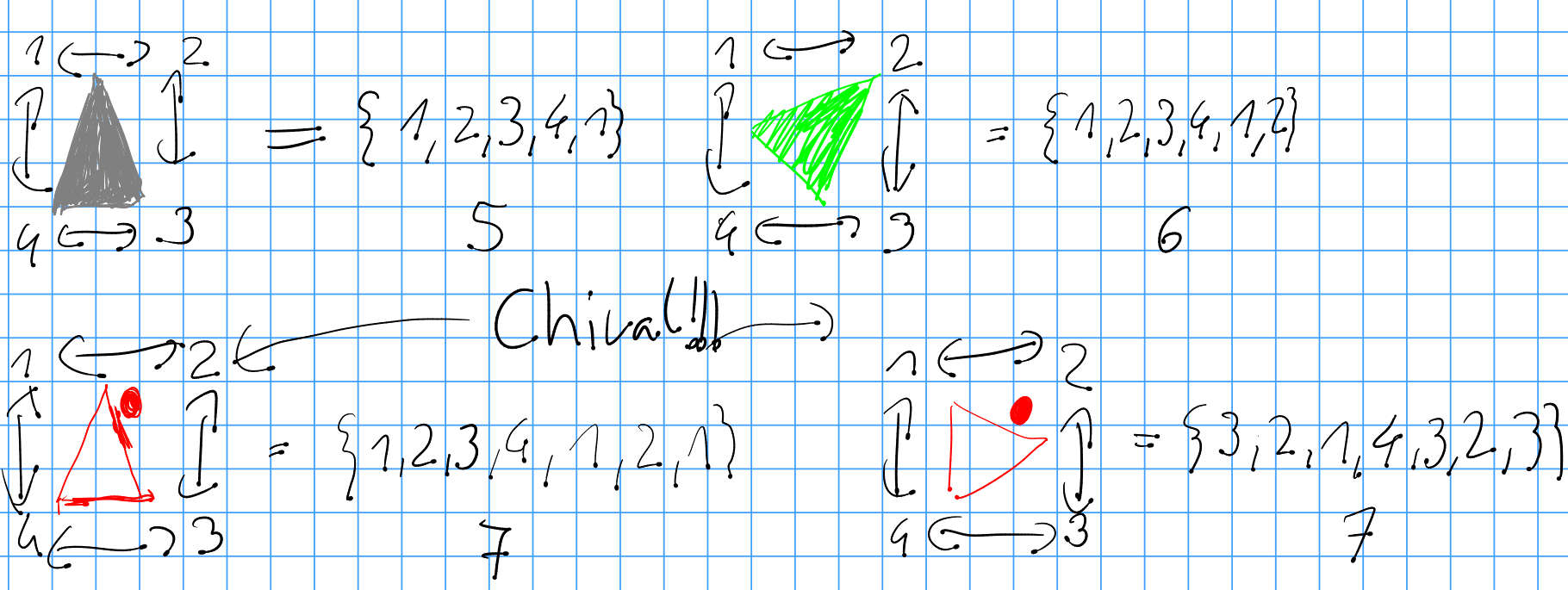
My represenations are not chiral, so i ran into problems with red, which could be solved by understanding that the problem was created by chirality.

![enter image description here][5]

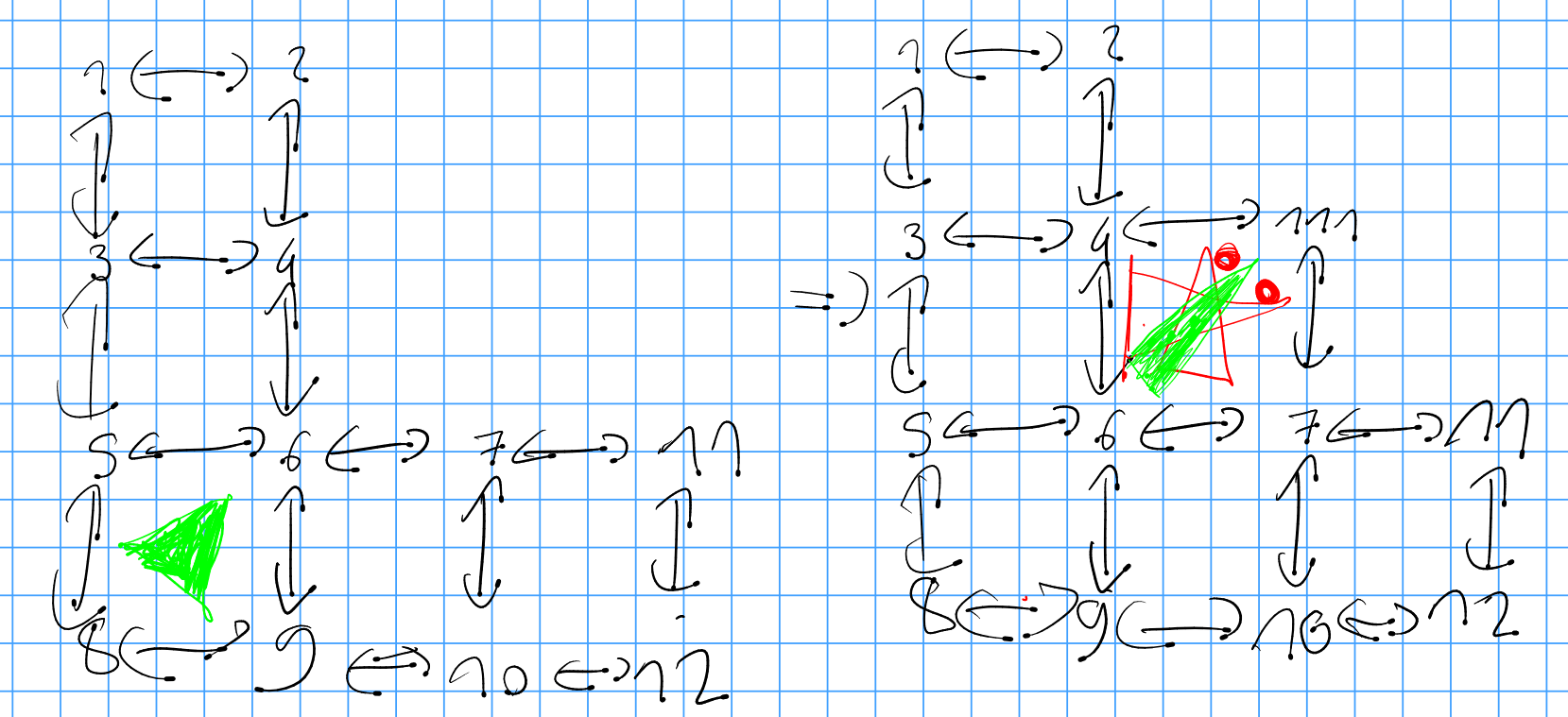
The dot always points away from the coordinate axis.

The code looks like that:

WolframModel[{
    {
     {5,6,9,8,5,6},
     {1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
     {4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
     {6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
     {6,7},{7,6},{7,10},{10,7},{10,9},{9,10},
     {7,11},{11,7},{11,12},{12,11},{12,10},{10,12}
    } -> {
     {4,111,7,6,4,111,4},
     {7,111,4,6,7,111,7},
     {4,111,7,6,4,111},
     {1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
     {4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
     {6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
     {6,7},{7,6},{7,10},{10,7},{10,9},{9,10},
     {7,11},{11,7},{11,12},{12,11},{12,10},{10,12},
     {4,111},{111,4},{111,7},{7,111}
    },
    {
     {6,7,10,9,6,7,6},
     {1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
     {4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
     {6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
     {6,7},{7,6},{7,10},{10,7},{10,9},{9,10}
    } -> {
     {4,111,7,6,4,111,4},
     {1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
     {4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
     {6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
     {6,7},{7,6},{7,10},{10,7},{10,9},{9,10},
     {4,111},{111,4},{111,7},{7,111}
    },
    {{1,2,3,4,1},{1,2},{2,1},{2,3},{3,2},{3,4},{4,3}}->
        {{11,12,2,1,11},{1,2},{2,1},{2,3},{3,2},{3,4},{4,3},{11,1},{1,11},{11,12},{12,11},{12,2},{2,12}}
},{
    {1,2,3,4,1},{2,3,4,1,2},{3,4,1,2,3},{4,1,2,3,4},
    {1,2,3,4,1,2},{2,3,4,1,2,3},{3,4,1,2,3,4},{4,1,2,3,4,1},
    {1,2},{2,1},{2,3},{3,2},{3,4},{4,3},{4,1},{1,4}
}
, 32, "FinalStatePlot"]

Thank You, Malthe Andersen,

after solving this toy problem, we can strive to attack bigger problems. The solution has more potential for optimization to run faster but now we can finaly say that we can build a 2d grid.