Are you aware of any initial conditions or rules for SetReplace that produces arbitrarily large patches of discretised R^2?

Are those defect free? (No Hyper edges or overlapping nodes)

How do you address the measurement issue problem on large enough graphs to exhaust our computation? Are there clever strategies to solve this issue?

Heureka. The solution was discovered thanks to Malthe Andersen who had an inspired solution in this thread: https://community.wolfram.com/groups/-/m/t/1946413

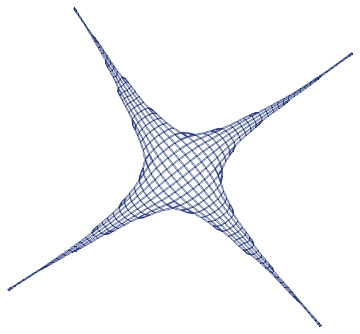
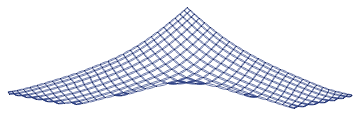
However you still got the problem of long tails.

I found it nicer to pre generate a (partial) pattern using just r1 and then fill is seperatly.

The current rules:

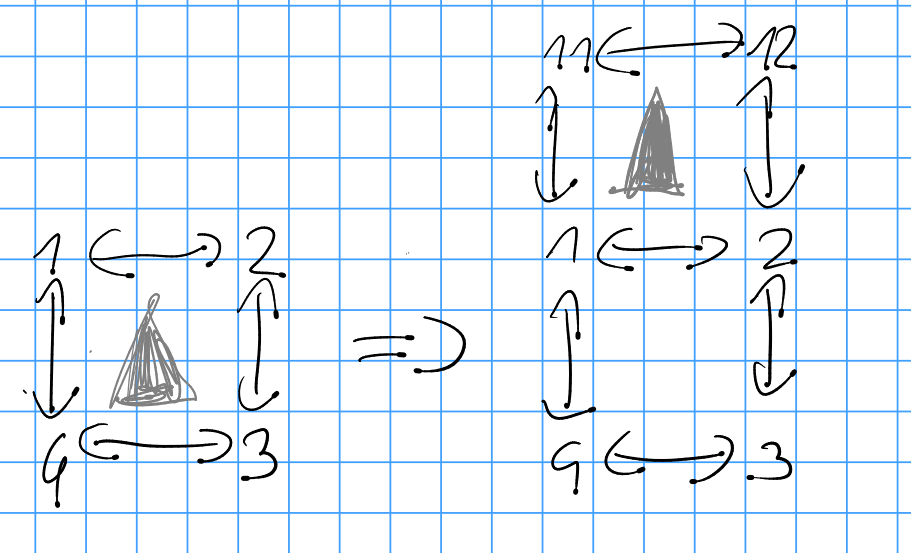
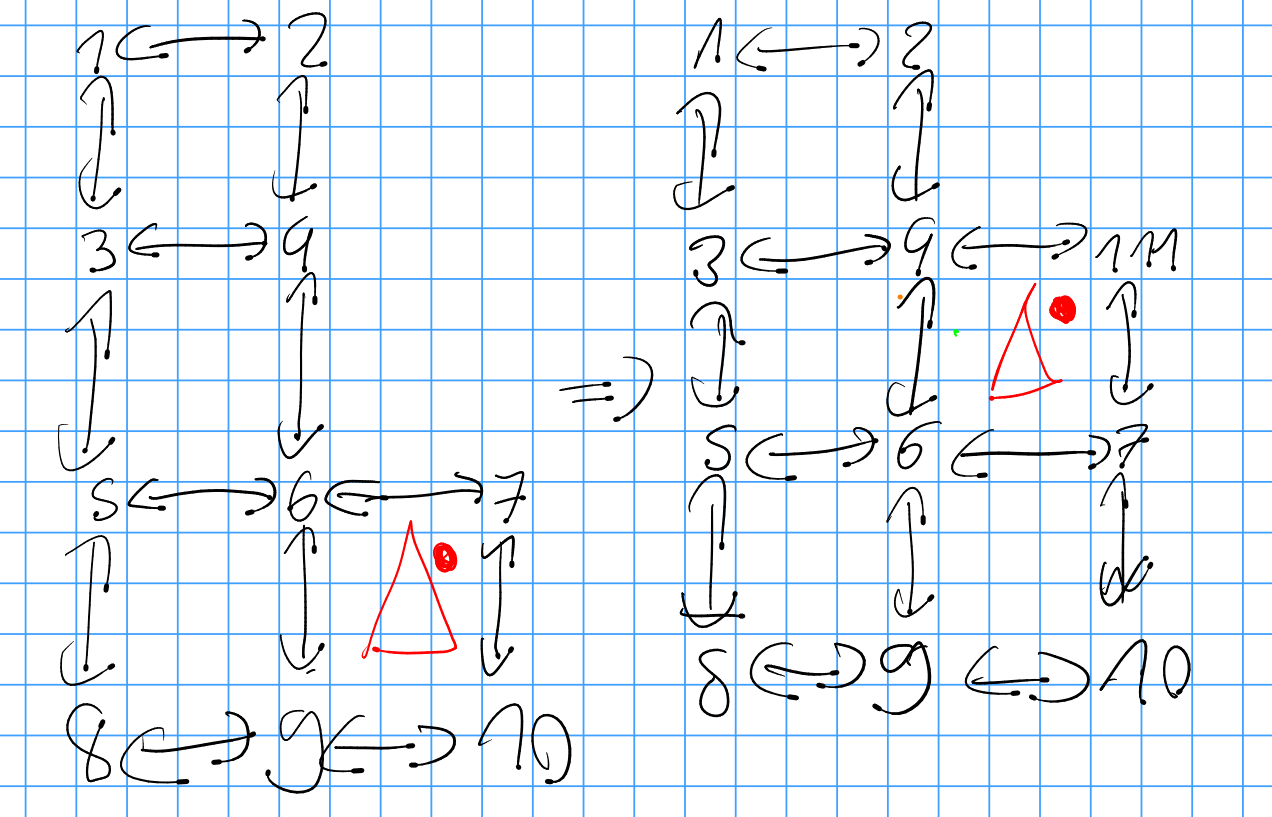
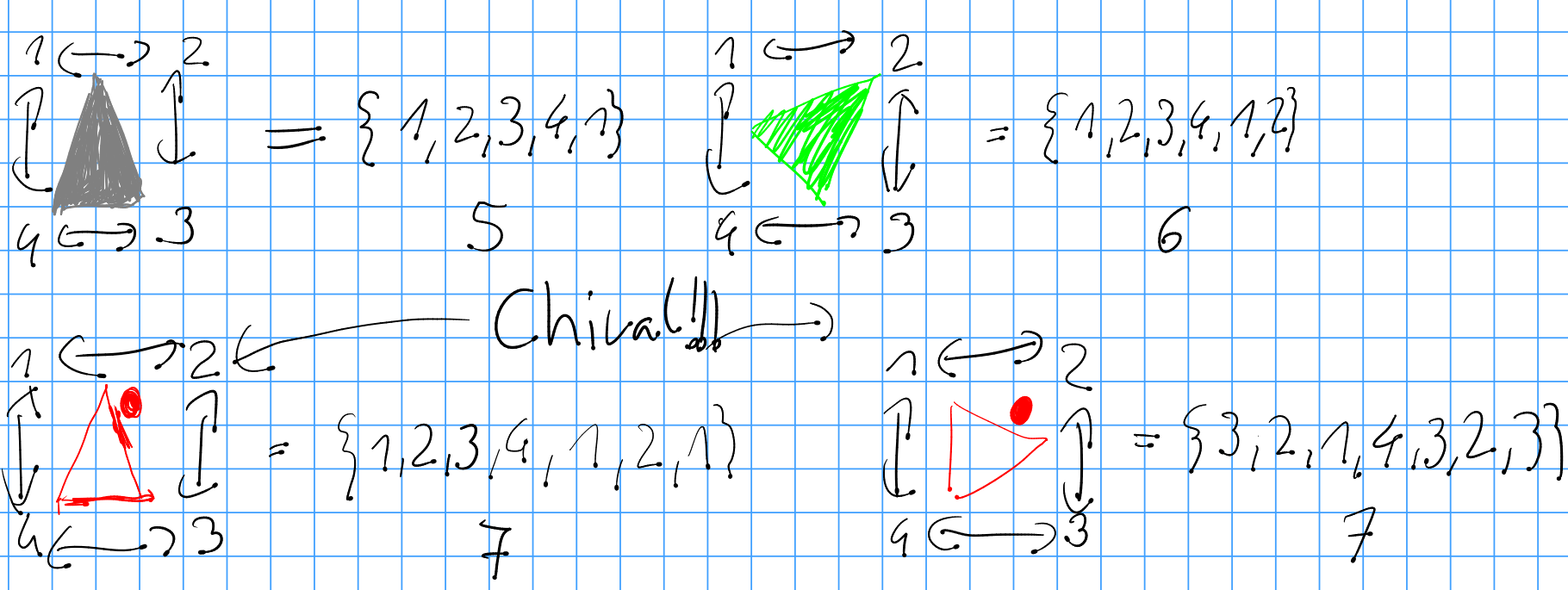
My represenations are not chiral, so i ran into problems with red, which could be solved by understanding that the problem was created by chirality.

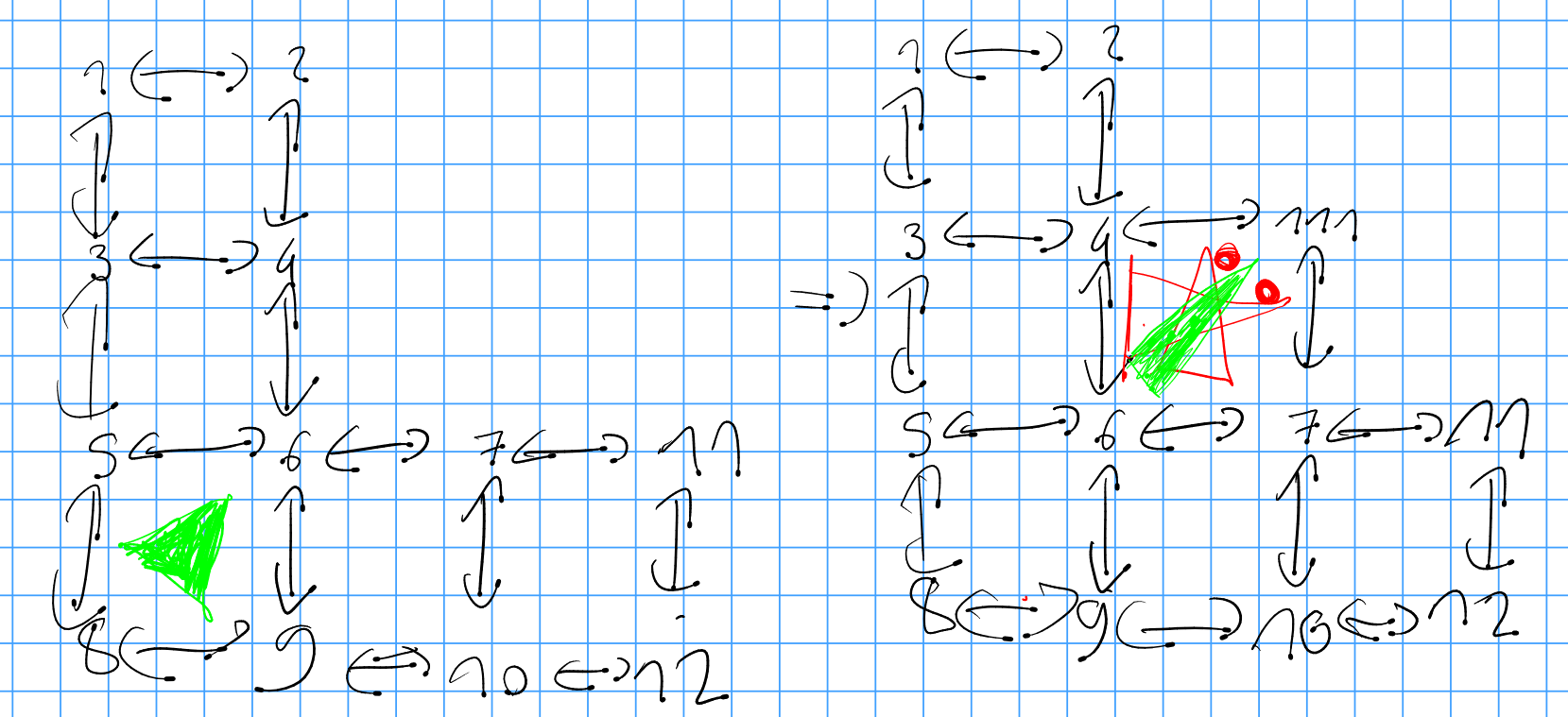
The dot always points away from the coordinate axis.

The code looks like that:

WolframModel[{
    {
     {5,6,9,8,5,6},
     {1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
     {4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
     {6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
     {6,7},{7,6},{7,10},{10,7},{10,9},{9,10},
     {7,11},{11,7},{11,12},{12,11},{12,10},{10,12}
    } -> {
     {4,111,7,6,4,111,4},
     {7,111,4,6,7,111,7},
     {4,111,7,6,4,111},
     {1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
     {4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
     {6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
     {6,7},{7,6},{7,10},{10,7},{10,9},{9,10},
     {7,11},{11,7},{11,12},{12,11},{12,10},{10,12},
     {4,111},{111,4},{111,7},{7,111}
    },
    {
     {6,7,10,9,6,7,6},
     {1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
     {4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
     {6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
     {6,7},{7,6},{7,10},{10,7},{10,9},{9,10}
    } -> {
     {4,111,7,6,4,111,4},
     {1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
     {4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
     {6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
     {6,7},{7,6},{7,10},{10,7},{10,9},{9,10},
     {4,111},{111,4},{111,7},{7,111}
    },
    {{1,2,3,4,1},{1,2},{2,1},{2,3},{3,2},{3,4},{4,3}}->
        {{11,12,2,1,11},{1,2},{2,1},{2,3},{3,2},{3,4},{4,3},{11,1},{1,11},{11,12},{12,11},{12,2},{2,12}}
},{
    {1,2,3,4,1},{2,3,4,1,2},{3,4,1,2,3},{4,1,2,3,4},
    {1,2,3,4,1,2},{2,3,4,1,2,3},{3,4,1,2,3,4},{4,1,2,3,4,1},
    {1,2},{2,1},{2,3},{3,2},{3,4},{4,3},{4,1},{1,4}
}
, 32, "FinalStatePlot"]

Thank You, Malthe Andersen,

after solving this toy problem, we can strive to attack bigger problems. The solution has more potential for optimization to run faster but now we can finaly say that we can build a 2d grid.