Great, I will test it.

That is the graph for the website, now you got it.

I have another challenge problem for you later.

Nice. I will study on it now.

Dear Michelle,

thank you for the matrix. Here are some comments. I first save the matrix

I then plot it.
Looks nice:


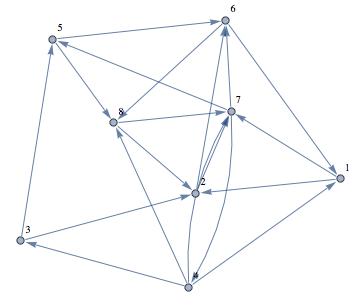
Next I calculate the eigenvalues - strictly speaking this is not necessary for your problem.
This gives

The normalised eigenvector to the largest (first) eigenvalue is obtained by

Now that gives the desired result
which are the relative times to spend at the different nodes.

If we normalise the sum to 1, we obtain the percentage of the time that a random walker would spend at a given node.
This gives
So about 12% of the time the random walker is at node one etc.
Just to check the result, let's use the power algorithm to determine the eigenvector. I define an arbitrary starting vector:
I then apply the matrix to the vector and iterate...say 100 times:
The result is 
which is identical to the one above. Normalising this to 1 in the numerically most clumsy way
gives the relative times spent at the nodes
I hope that this helps. Note that it does not take the probabilities that you gave into consideration. 

M.

Dear Michelle,

No, that is not surprising. After all, we are performing a random walk on the network. Everytime you run it it will give you a different sequence of websites.


I am not sure what mini-web you are referring to; can you upload the figure? If you are given a simple (toy) network, you would proceed as Sean Clarke has suggested. You would use Markov. So probably you want to find the eigenvector to the dominant eigenvalue. The values of the components of the vector will give you the relative times spent on the websites.

M.

Do you have your email address, so I can sent the real question to you. SInce I still confuse something and I don't know how to load the pdf picture in the quesion here.

I just ran exactly your code (copy and paste), but it came out a straight line with a circle. Is it strange?

Hi, Here is the code I have, what do you think about this one?

The idea:

1. Create a function that takes in a number of iterations to run for.
2. Use the "Module to create a list of variables you'll need to use in the function. One of these must be a counter to keep track of how many times you've hit each website.




rankwebsite[n_] :=
Module[{a, b, c, list, count = {0, 0, 0, 0, 0, 0, 0, 0}},
 
  (*3. Create a list that represents the network inside the function*)
\

 
  list = {};
  
   (*4. Generate a website to start with using the RandomInteger \
function*)
  
   a = RandomInteger[{1, 8}];
  
   (*5. Increase the counter for that website in your count by 1*)
  
   count[] = count[] + 1;
  
   (*6. Create a for loop to go through the iterations*)
  
   For[i = 1, i <= n, i++,
   
    (*7. Create another RandomInteger to store the probability*)
   
    b = RandomInteger[{1, 100}];
   
    (*8. If the probability is from 85-100,
    you  want to go to another random website,
    so you reset your initial variable,a,
    and increase its counter by 1 as before. Otherwise,
    go to a website linked to the website you're currently on*)
   
    If[b > 85,
    
     a = RandomInteger[{1, 8}];
     count[] count[] + 1;,
    
     c = RandomInteger[]; (*Access a number for the linked website \
you will now go to*)
     a = list[][];
     count[] = count[] + 1; (*Increase counter again*)
     ];
   
    ];
  
   (*Now all you have to do is print out the websites in such a way \
that you see the rankings clearly*)
  
   ;]

To: Vote 1,

When I use your code, I got something like

Graph::supp: Mixed graphs and multigraphs are not supported. >>

I couldn't figure out where the something I have to fix.

Thanks

There is also a quite nice book on this: "A Course on the Web Graph" by Anthony Bonato published by the American Mathematical Society. Many of the ideas in that book can be efficiently implemented in Mathematica. 

Actually, there are page ranking methods which aare based on this kind of thing, i.e. HITS (hyperlink-induced topic search), the well known page rank, and SALSA (Stochastic Approach for Link Structure Analysis). PageRank is sort of the stationary distribution of a random walk on a digraph; it represents the probability that a random surfer visits the page. The algorithm is just as you describe, i.e. a random walk with some probability of jumping to a completely unrelated page. 

On page 107 of "A Course on the Web Graph" you find a theorem that shows how the dominant eigenvector s, i.e. the one with eigenvalue 1, of the (suitably defined) transition matrix, is crucial here. The PageRank Markov Chain converges to a stationary distribution equalling s. 
Once the transition matrix is known it is, in theory, straight forward to calculate the dominant eigenvector with Mathematica.

Of ocurse there are the obvious limits for extremely large graphs. Mathematica estimates the number of websites 
to be roughly 10.82 billion as of May 2012. I suppose that in order to calculate the dominant eigenvector for the "entire network" there are substantial numerical difficulties on standard computer systems, even if we use sparse matrices. It appears that Google use the power iteration scheme to calculate the page rank; this takes a week or so of intensive calculations on quite powerful computer systems. There are algorithms based on Monte Carlo approaches which converge quite quickly and can be easily parallelised:
http://www-sop.inria.fr/members/Konstantin.Avratchenkov/pubs/mc.pdf

Cheers,
M.

NB: The google toolbar allows you to see the PageRank of any given website:
https://support.google.com/toolbar/answer/79837?hl=en-GB

Actually, can we use the

Monte Carlo Simulation to determine the percentage of time a user spends at each of the eight sites ? Thanks.

Dear Michelle,

you might want to try this code:

A standard output would be:



There are lots of obvious ways to improve this. Also it does not include the 15% probability to jump to a random website yet, but that is straight forward to program into it.

You can for example use
http://www.randomwebsite.com/cgi-bin/random.pl
and jump to where that redirects to get a new fresh starting site for your random walk.

Cheers,
M.