
Curved mirrors are exciting because of their interesting deformations. But geometrically perfect curved mirrors are not easy to come by. Cylindrical mirrors can be hand made relatively simple with reflective film but conical mirrors require machining or 3D printing and chemical chrome plating. Luckily, we have spherical mirrors and around Christmas, they are everywhere! I bought a new set of these and used Mathematica to study some new features of reflection and anamorphosis.
I made two functions for a convex sphere-shaped mirror with radius 1 (here called a "spherical mirror") and a viewpoint at infinity. The relatively small size of the mirror compared to the view distance simplifies the functions considerably:
a function for reflection: sphericreflectionMap[{x,y},h] will find the (virtual) reflection R of the point S {x,y,h} located in the plane z=h
a function for its inverse: sphericAnamorphosisMap[{y,z},h] will compute the coordinates of a point S in the plane z=h reflecting as point R{0,y,z}.
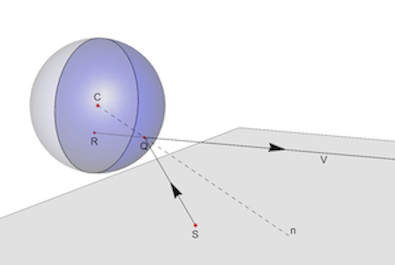
Applying the law of reflection: a point S on a plane z=h emits a light ray reflected by the mirror at Q and the eye at V observes the point as R. n is the normal to the sphere at Q and the angles SQN and VQn are equal.
sphericReflectionMap[{xs_, ys_}, h_ : 1] :=
Quiet[Module[{ptC = {0, 0, 0}, plane, ptQ, solI, xv = 1000000},
plane = InfinitePlane[{ptC, {xv, 0, 0}, {xs, ys, h}}];
ReplacePart[
First[{x, y, z} /.
NSolve[{{x, y, z} \[Element] Sphere[], {x, y, z} \[Element]
plane, x Sqrt[(x - xs)^2 + (y - ys)^2 + (z - h)^2] == -x^2 +
x xs - y^2 + y ys + z (-z + h), x > 0}]], 1 -> 0]]]
sphericAnamorphosisMap[{yi_, zi_}, h_ : 1] :=
Module[{x, y, z, sh, ptI, ptV, solQ, ptQ, eqns, sol},
sh = Sign[zi] Abs[h]; ptV = {1000000, 0, 0};
solQ = NSolve[{x, y, z} \[Element]
HalfLine[{{0, yi, zi}, ptV}] && {x, y, z} \[Element]
Sphere[], {x, y, z}]; ptQ = First[{x, y, z} /. solQ];
eqns = {RegionMember[
HalfLine[{ptQ, ReflectionTransform[ptQ][-ptV]}], {x, y, sh}],
RegionMember[
InfinitePlane[{{0, 0, sh}, {1, 0, sh}, {0, 1, sh}}], {x, y,
sh}]}; sol = Quiet[NSolve[eqns, {y, x}][[1]]]; {x, y, sh} /.
sol]
The two above functions are the inverse of each other. For example each new random point pnt in the plane z=2 will be reflected as a point whose anamorphic map is again the same point pnt. This computes the (negligible) difference between the two pnt:
With[{r = 10, h = 2}, pnt = RandomPoint[Rectangle[{-r, -r}, {r, r}]];
Most[sphericAnamorphosisMap[Rest[sphericReflectionMap[pnt, h]], h]] -
pnt]
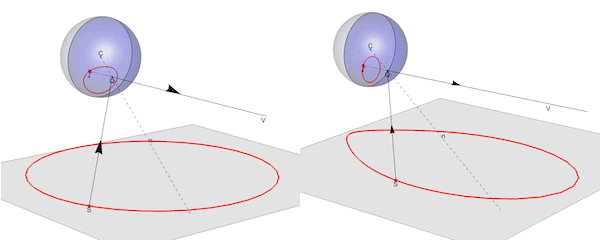
This is an example of application of the functions: 1. left : a circle in the plane z=-2.5 is reflected as an oval shaped curve, computed by sphericReflectionMap 2 right: an oval curve in z=-2.5, computed by sphericAnamorphosisMap is reflected as a circle in a spheric mirror
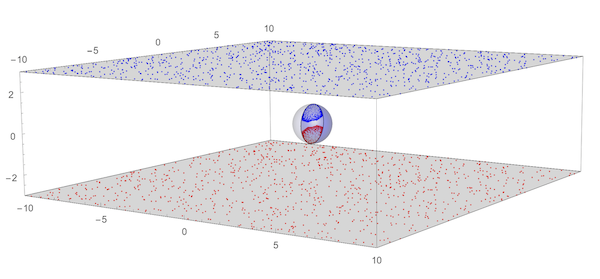
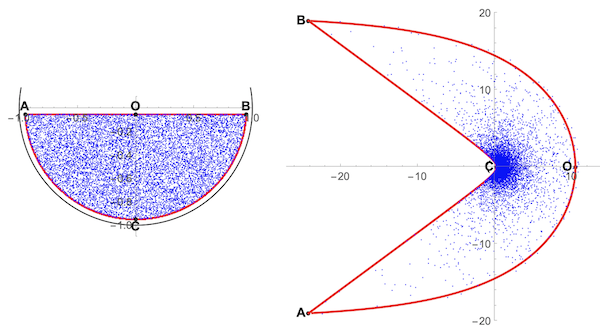
It can be observed that all of our surrounding space is reflected in a sphere shaped mirror. We can explore this by looking for the range and domain of the functions sphericReflectionMap and sphericAnamorphosisMap using random points . This shows the reflection in a spherical mirror of 1000 random points in the planes z=-2 and z=+2. Even if we extend the domain to the complete infinite planes z=+/-2, the range is limited to the upper or lower half-disks inside the mirror.
Module[{h = 3, r = 10, n = 1000, pnts, reflectedPntsBotttom,
reflectedPntsTop},
pnts = RandomPoint[Rectangle[{-r, -r}, {r, r}], n];
reflectedPntsBotttom =
ParallelMap[sphericReflectionMap[#1, -h] &, pnts];
reflectedPntsTop = ParallelMap[sphericReflectionMap[#1, h] &, pnts];
mirror = {{Opacity[.15], Lighter[Blue, .75],
Sphere[]}, {Opacity[.25],
Style[Sphere[], Blue, Specularity[White, 25],
ClipPlanes ->
InfinitePlane[{{0, 0, 0}, {0, 1, 0}, {0, 0,
1}}]]}, {Opacity[.2],
Cylinder[{{-.01, 0, 0}, {0, 0, 0}}, 1]}};
Graphics3D[{mirror, {Opacity[.25], (InfinitePlane[{{0, 0, #1}, {1,
0, #1}, {0, 1, #1}}] &) /@ {-h, h}}, AbsolutePointSize[1.5],
Red, Point[pnts /. {x_, y_} -> {x, y, -h}], Blue,
Point[pnts /. {x_, y_} -> {x, y, h}], AbsolutePointSize[.75], Red,
Point[reflectedPntsBotttom], Blue, Point[reflectedPntsTop]},
Lighting -> "Accent", PlotRange -> {{-10, 10}, {-10, 10}, {-h, h}},
Axes -> True]]
Points at infinity are reflected on the rim of the reflection half-disks. Points on the rim of the half-disk have their anamorphic map at infinity. For all practical applications, we have to stay away from the rims. This shows the four keypoints along the rim of the lower reflection half-disk (left) and their anamorphic map (right).
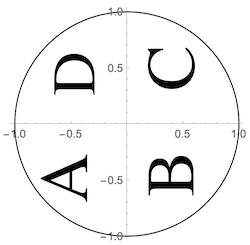
A first practical test of our functions is to fill up the two half-disks to a reasonable distance from the rim. Below is a help function to convert a letter to a FilledCurve with provisions for scaling (sc) and centering (dx,dy). Since FilledCurve is not supported in 3D, we convert the FilledCurve to a Line object.
horizontalLetter2D[lt_, sc_, dx_, dy_] :=
First[First[
ImportString[
ExportString[Style[lt, FontFamily -> "Times", FontSize -> 72],
"PDF"], "TextMode" -> "Outlines"]]] /. {x_?NumericQ, y_} :>
RotationMatrix[Pi/2] . {x, y}/sc /. {x_?NumericQ,
y_} :> {x + dx, y + dy};
horizontalLetter3D[lt_, sc_, dx_, dy_] :=
horizontalLetter2D[lt, sc, dx,
dy] /. {x_?NumericQ, y_?NumericQ} :> {0, x, y} /.
FilledCurve[a_, b_] -> Line[b]
Graphics[{Circle[], horizontalLetter2D["A", 85, -.2, -.7],
horizontalLetter2D["B", 85, +.75, -.65],
horizontalLetter2D["C", 85, +.75, .3],
horizontalLetter2D["D", 95, -.15, .25]}, Axes -> True,
ImageSize -> Small]
anaHorizontalLetter2D[lt_, sc_, dx_, dy_] :=
MapAt[Most[sphericAnamorphosisMap[#1, 3]] &,
horizontalLetter2D[lt, sc, dx, dy], {-1, 1, 1, -1, All, All}]
anaHorizontalLetter3D[lt_, sc_, dx_, dy_] :=
MapAt[sphericAnamorphosisMap[#1, 3] &,
horizontalLetter2D[lt, sc, dx, dy], {-1, 1, 1, -1, All, All}] /.
FilledCurve[a_, b_] -> Line[b]
Graphics3D[{{Opacity[.25], {{Opacity[.15], Lighter[Blue, .75],
Sphere[]},
Style[Sphere[], Blue, Specularity[White, 25], Opacity[.13],
ClipPlanes ->
InfinitePlane[{{0, 0, 0}, {0, 1, 0}, {0, 0,
1}}]]}}, {horizontalLetter3D["A", 85, -.2, -.7],
horizontalLetter3D["B", 85, +.75, -.65],
horizontalLetter3D["C", 85, +.75, .3],
horizontalLetter3D["D", 95, -.15, .25]} /.
Thickness[_] :>
AbsoluteThickness[1], {anaHorizontalLetter3D["A", 85, -.2, -.7],
anaHorizontalLetter3D["B", 85, +.75, -.65],
anaHorizontalLetter3D["C", 90, +.75, .3],
anaHorizontalLetter3D["D", 105, -.15, .25]} /.
Thickness[_] :> AbsoluteThickness[3], {AbsoluteThickness[2],
Line[{{-6, -8, -3}, {-6, 6, -3}, {6,
6, -3}, {7, -8, -3}, {-6, -8, -3}}],
Line[{{-6, -8, 3}, {-6, 6, 3}, {6, 6, 3}, {7, -8, 3}, {-6, -8,
3}}]}}, PlotRange -> {{-6, 7}, {-8, 6}, {-3, 3}},
Boxed -> False]

Above, we have the printout of the previous code (L) and the real world reflection in a Christmas ball hanging between two prints of the converted anamorphic letters (R). Now, we are ready to reflect two famous Christmas symbols in our Christmas-ball mirror. First the Xmas tree: these 15 points define the outline of a tree to be reflected in the lower half-disk:
xmasTree = {{-0.714, -0.571}, {-0.286, -0.771`}, {-0.286, -0.671`}, \
{0., -0.857}, {0.`, -0.714`}, {0.286, -0.9`}, {0.28600, -0.614`}, \
{0.571, -0.671`}, {0.571, -0.471}, {0.286, -0.529`}, {0.286, \
-0.243`}, {0.`, -0.429`}, {0., -0.286}, {-0.286, -0.471}, {-0.286, \
-0.371`}, {-0.714, -0.571}};
Graphics[{Circle[], FaceForm[Green], EdgeForm[AbsoluteThickness[3]],
Polygon[xmasTree]}, Axes -> True]
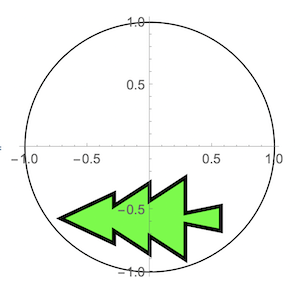
To get the correctly reflected shape, we need to interpolate a sufficient number of points between the original ones. The following function will interpolate enough points between pnt1 and pnt2 to reduce the distance between them to d. Applied to the original 15, this results in 90 points and a more accurate reflection if sphericAnamorphosisMap is applied resulting in curved lines between the original 15 keypoints:
interpol[{pnt1 : {x1_, y1_}, pnt2 : {x2_, y2_}}, d_ : 0.1] :=
Module[{n}, n = EuclideanDistance[pnt1, pnt2]/d + 0.001`;
Table[(1 - t) pnt1 + t pnt2, {t, 0, 1, 1/n}]]
xmasTreePoints = (interpol[#1, .05] &) /@
Partition[xmasTree, 2, 1, {1, 1}];
anaXmasTreePoints =
ParallelMap[Most[sphericAnamorphosisMap[#1, 2]] &,
xmasTreePoints, {2}] /. {x_?NumericQ, y_} -> {x, -y};
Graphics[{FaceForm[Green], EdgeForm[AbsoluteThickness[5]],
Polygon[Flatten[anaXmasTreePoints, 1]]}]

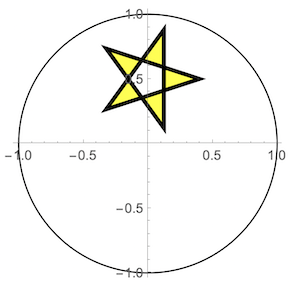
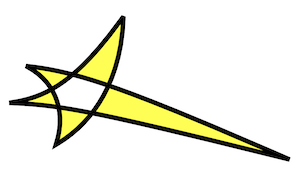
We do the same actions for a star shape to be reflected in the upper half-disk...
xmasStar =
Table[{Cos[(2 Pi k 2)/5.], Sin[(2 Pi k 2)/5.]}, {k,
5}] /. {x_?NumericQ, y_} -> {x, y + 1.25}/2.5;
Graphics[{Circle[], FaceForm[Yellow], EdgeForm[AbsoluteThickness[3]],
Polygon[xmasStar]}, Axes -> True]
xmasStarPoints =
interpol[#, .05] & /@ Partition[xmasStar, 2, 1, {1, 1}];
anaXmasStarPoints =
ParallelMap[Most[sphericAnamorphosisMap[#, 2]] &,
xmasStarPoints, {2}] /. {x_?NumericQ, y_} -> {x, -y};
Graphics[{FaceForm[Yellow], EdgeForm[AbsoluteThickness[5]],
Polygon@Flatten[anaXmasStarPoints, 1]}]
... and we put it all together in a Graphics3D (L) and in a real world setup reflected in a hanging Christmas ball!
Graphics3D[{mirror, {{FaceForm[Green], EdgeForm[AbsoluteThickness[1]],
Polygon@
Flatten[xmasTreePoints, 1] /. {x_?NumericQ, y_} -> {0, -x, -y},
EdgeForm[AbsoluteThickness[3]],
Polygon@Flatten[anaXmasTreePoints, 1] /. {x_?NumericQ, y_} -> {-x,
y, 2}}}, {{FaceForm[Orange], EdgeForm[AbsoluteThickness[1]],
Polygon@Flatten[xmasStarPoints, 1] /. {x_?NumericQ,
y_} -> {0, -x, -y}, EdgeForm[AbsoluteThickness[3]],
Polygon@Flatten[anaXmasStarPoints, 1] /. {x_?NumericQ, y_} -> {-x,
y, -2}}}, {AbsoluteThickness[3],
Line[{{-6, -5, -2}, {-6, 6, -2}, {6,
6, -2}, {7, -5, -2}, {-6, -5, -2}}],
Line[{{-6, -5, 2}, {-6, 6, 2}, {6, 6, 2}, {7, -5, 2}, {-6, -5,
2}}], AbsoluteThickness[2], Blue,
Line[{{0, 1, 0}, {0, 6, 0}}]}}, Boxed -> False, ImageSize -> 250]
