Following Bill,
In[1]:= data = {{0, 2.52}, {1., 2.83}, {2., 3}, {3., 3.2}, {4.1,
3.35}, {5., 3.47}, {6, 3.57}, {7, 3.66}, {8, 3.76}, {8.5,
3.81}, {9, 3.85}, {9.5, 3.89}, {10.1, 3.94}, {10.5, 3.98}, {11,
4.01}, {11.5, 4.06}, {12, 4.09}, {12.5, 4.15}, {13, 4.19}, {13.5,
4.25}, {14, 4.3}, {14.5, 4.35}, {15, 4.41}, {15.6, 4.47}, {16,
4.53}, {16.5, 4.6}, {17., 4.68}, {17.5, 4.77}, {18, 4.85}, {18.5,
4.96}, {19, 5.11}, {19.55, 5.34}, {19.7, 5.44}, {19.9,
5.58}, {20.1, 5.91}, {20.3, 6.27}, {20.5, 7.14}, {20.6,
7.14}, {20.8, 7.81}, {20.9, 8.32}, {21, 7.75}, {21.2,
9.07}, {21.4, 9.49}, {21.5, 9.71}, {21.6, 9.83}, {21.8, 10}, {22,
10.18}, {22.1, 10.21}, {22.2, 10.25}, {22.3, 10.27}, {22.5,
10.3}, {22.7, 10.42}, {22.9, 10.47}, {23.1, 10.52}, {23.3,
10.59}, {23.5, 10.63}, {23.7, 10.67}, {24, 10.74}, {24.2,
10.78}, {24.4, 10.8}, {24.6, 10.82}, {24.8, 10.84}, {25, 10.87}};
In[2]:= dplot = ListPlot[data, PlotStyle -> Red];
In[3]:= eq = .1 x + b/(1 + Exp[-c (x - x0)]) + d;
In[4]:= pars = FindFit[data, eq, {b, c, d, x0}, x]
Out[4]= {b -> 5.38732, c -> 2.16503, d -> 2.92208, x0 -> 20.7642}
In[5]:= Show[Plot[eq /. pars, {x, 0, 25}], dplot, PlotRange -> All]
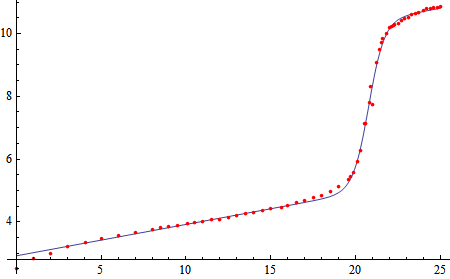
I put the 0.1 x in manually -- Mathematica does not seem very good at finding the value for itself.
Best,
David