Group Abstract Group Abstract

Message Boards Message Boards

1
|
227K Views
|
6 Replies
|
2 Total Likes
View groups...
Share
Share this post:

$\int_0^\infty e^{i \pi x} \left(1-(x+1)^{\frac{1}{x+1}}\right) dx$

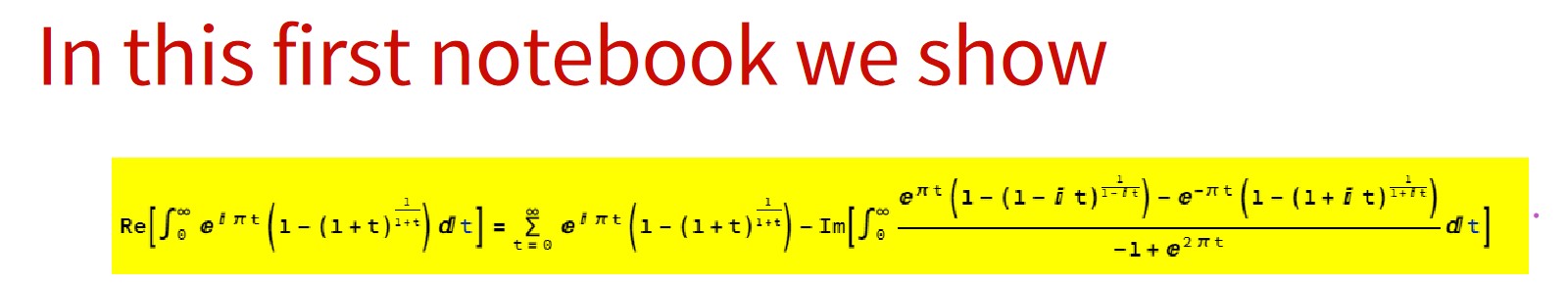
$\int_0^\infty e^{i \pi x} \left(1-(x+1)^{\frac{1}{x+1}}\right) dx$ enter image description here enter image description here

enter image description here

f[x_] = E^(I*Pi*x)*(1 - (x + 1)^(1/(x + 1))); 
g[x_] = x^(1/x); u := t/(1 - t); 

sub = Im[NIntegrate[(f[(-I t)] - f[( I t)])/(Exp[2 Pi t] - 1), {t,
          0, Infinity}, WorkingPrecision -> 100]]

0.1170836031505383167089899122239912286901483986967757585888318959258587743002\
7817712246477316693025869

m = NSum[f[( t)] , {t, 0, Infinity}, WorkingPrecision -> 100, 
  Method -> "AlternatingSigns"]

0.1878596424620671202485179340542732300559030949001387861720046840894772315646\
6021370329665443217278

m - sub

0.0707760393115288035395280218302820013657546962033630275831727881636184572643\
8203658083188126524252

Is the same as 


{Re[NIntegrate[f[t], {t, 0, Infinity}]], and, 
 Re[NIntegrate[f[t], {t, 0, Infinity I}, WorkingPrecision -> 100]]}

NIntegrate::deodiv: DoubleExponentialOscillatory returns a finite integral estimate, but the integral might be divergent.

NIntegrate::deodiv: DoubleExponentialOscillatory returns a finite integral estimate, but the integral might be divergent.

{0.070776, and, \
0.0707760393115288035395280218302820013657546962033630275831727881636184572643\
8203658083188126617723821}

To be continued.
POSTED BY: Marvin Ray Burns A.G.S. (cum laude)
6 Replies
Sort By:
POSTED BY: Marvin Ray Burns A.G.S. (cum laude)

POSTED BY: Marvin Ray Burns A.G.S. (cum laude)

POSTED BY: Marvin Ray Burns A.G.S. (cum laude)

So, I could conclude that enter image description here

The following "proof of it is from combining

https://www.quora.com/Why-is-it-that-f-x-e-i-pi-x-left-1-x-1-frac-1-x-1-right-int0-infty-f-t-dt-i-int0-infty-f-i-t-dt

and

https://www.quora.com/How-would-you-prove-for-g-x-x-1-x-lim-limits-N-to-infty-int-limits1-2N-e-i-pi-t-g-t-dt-i-lim-limits-N-to-infty-int-limits-0-2N-frac-g-1-it-exp-pi-t-dt.

Whileenter image description here enter image description here

enter image description here Something similar is shown: enter image description here enter image description here enter image description here enter image description here enter image description here enter image description hereenter image description here enter image description here

That looks like it proves it to me. But I don't see any proof for this.
POSTED BY: Marvin Ray Burns A.G.S. (cum laude)

I won't bring the subject of numerical computation into this discussion, but I spent several years learning to compute the digits of $\int_0^\infty{e^{i \pi x} \left(1-(x+1)^{\frac{1}{x+1}}\right)}dx.$ You can read about my adventure at How to calculate the digits of the MKB constant. If you like numeric computations, of much interest is the story of how I came across this integral, by investigating $\sum _{x=0}^{\infty } e^{i \pi x} \left(1-(x+1)^{\frac{1}{x+1}}\right)$ since the 1990s, at Try to beat these MRB constant records!
POSTED BY: Marvin Ray Burns A.G.S. (cum laude)

POSTED BY: Marvin Ray Burns A.G.S. (cum laude)
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard