$\int_0^\infty e^{i \pi x} \left(1-(x+1)^{\frac{1}{x+1}}\right) dx$ 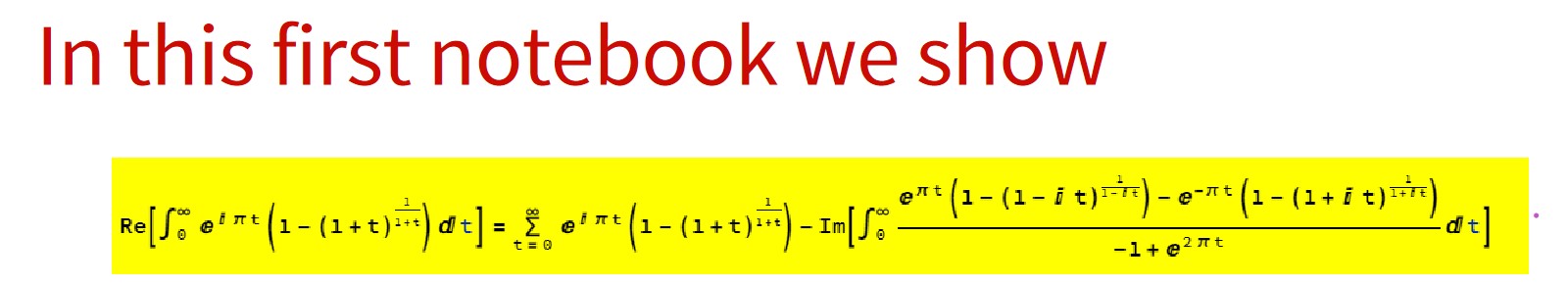


f[x_] = E^(I*Pi*x)*(1 - (x + 1)^(1/(x + 1)));
g[x_] = x^(1/x); u := t/(1 - t);
sub = Im[NIntegrate[(f[(-I t)] - f[( I t)])/(Exp[2 Pi t] - 1), {t,
0, Infinity}, WorkingPrecision -> 100]]
0.1170836031505383167089899122239912286901483986967757585888318959258587743002\
7817712246477316693025869
m = NSum[f[( t)] , {t, 0, Infinity}, WorkingPrecision -> 100,
Method -> "AlternatingSigns"]
0.1878596424620671202485179340542732300559030949001387861720046840894772315646\
6021370329665443217278
m - sub
0.0707760393115288035395280218302820013657546962033630275831727881636184572643\
8203658083188126524252
Is the same as
{Re[NIntegrate[f[t], {t, 0, Infinity}]], and,
Re[NIntegrate[f[t], {t, 0, Infinity I}, WorkingPrecision -> 100]]}
NIntegrate::deodiv: DoubleExponentialOscillatory returns a finite integral estimate, but the integral might be divergent.
NIntegrate::deodiv: DoubleExponentialOscillatory returns a finite integral estimate, but the integral might be divergent.
{0.070776, and, \
0.0707760393115288035395280218302820013657546962033630275831727881636184572643\
8203658083188126617723821}
To be continued.