Group Abstract Group Abstract

Message Boards Message Boards

How can I do the output waveform of Schmitt trigger circuit?

POSTED BY: Jairo Smith Quilumbaquin Lanchimba
3 Replies
Sort By:

I guess this is because the discretization is too coarse. If you use a finer resolution, things will improve. Try e.g.:

state = -1;
xrange = {x, 6.5, 9, .01};
dataSchmitt = Table[{x, schmitt[Sin[x]]}, Evaluate@xrange];
dataSin = Table[{x, Sin[x]}, Evaluate@xrange];

ListLinePlot[{dataSchmitt, dataSin}, GridLines -> {None, {vl, vh}}, PlotRange -> {.5, 1}, AspectRatio -> .2]

enter image description here

ADDENDUM:

As I just found out you do can use Plot - but with the proper options:

state = -1;
Plot[{schmitt[Sin[x]], Sin[x]}, {x, 0, 4 Pi}, MaxRecursion -> 0, PlotPoints -> 200]

Without recursion all data points are evaluated in order.
POSTED BY: Henrik Schachner

Jairo,

this is an interesting problem! Here is a simple outline how it could be done:

vccPlus = 1;
vccMinus = -1;
vh = 0.75;
vl = -0.75;
schmitt[x_] := Which[(state == -1) && (x > vh), (state = 1; vccPlus),
  (state == 1) && (x > vl), vccPlus,
  (state == 1) && (x < vl), (state = -1; vccMinus),
  (state == -1) && (x < vh), vccMinus]

Using this with some proper initialization:

state = -1; (* "quick and dirty" initialization - just for the example! *)
dataSchmitt = Table[{x, schmitt[Sin[x]]}, {x, 0, 4 Pi, .1}];
dataSin = Table[{x, Sin[x]}, {x, 0, 4 Pi, .1}];

ListLinePlot[{dataSchmitt, dataSin}, GridLines -> {None, {vl, vh}}]

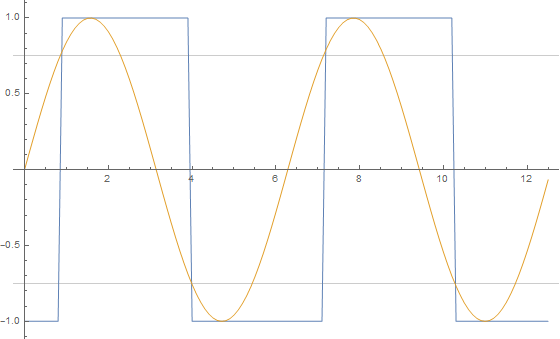
enter image description here

For this method to work it is necessary that the function points are evaluated in order (from left to right, so to speak). For this reason I generate explicit values and use ListLinePlot. Using simply

state = -1;
Plot[{schmitt[Sin[x]], Sin[x]}, {x, 0, 2 Pi}]

does not work in a clean way, because here there is no clear order of evaluation.

I am curious myself how this could be done in a better and more robust way!
POSTED BY: Henrik Schachner

Hi man, thanks for the method, I have a question: why exist a kind of delay in the positive Vcc, the negative Vcc is fine, it would be for the number of points? enter image description here

Thanks for help, thank you very much.
POSTED BY: Jairo Smith Quilumbaquin Lanchimba
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard