Hi Frederick, thanks for the thoughtful response.
I still can not run through your code, different Mathematica version (
I use 12.3 Chinese Version), but understand your RGB voxel puzzle
better.
Curious if the problem is with rasterize or system fonts or something else. I double checked on the cloud and got a totally wacky output:

Magnified
$10\times$ and "Antialiasing" is not an option for rasterize: "returns a rasterized version of the displayed form of expr". Suspicious behavior. Apple Safari seems to have the best display functions for CJK Unified Ideographs, see for example 道.
Otherwise, I think the code is okay when the input to function Partials is a set of
$14 \times 14$ binary matrices. You suggest going smaller, but I would even consider going to
$16 \times 16$ just to get a round power of two. The size of the space doesn't matter, only the size of the subspace containing non-zero values. For now leaving dimesnions as is, but later (especially when working with higher precision characters) it would be better to have adaptive sizing.
Your intuition is correct that the final theorem will involve conditionals, and I will now give a few counterexamples to show that dimensions of bounding box of non-zero subspace is an important concept in predicting output quality.
First, let me explain the math logic behind Partials, because it is kind of difficult to read in compact form. Say that we have three plane arrays of some square size, call them
$Z,X,Y$, with letter indicating normal vector direction in a Cartesian
$(x,y,z)$ system. Let each array contain a character pattern with binary values only,
$1$ for presence (有),
$0$ for absence (無). The way to create a positive 3D ambigram is simply to multiply values and find a set, call it
$$A = \langle (i,j,k) \in \mathbb{Z}^3 : Z(i,j)X(j,k)Y(k,i) = 1 \rangle . $$
This would be good enough to calculate the monotone ABC ambigram from wikipedia. Indeed, the function Partials calculates
$A$ first, but also calculates three supersets, which possibly intersect on
$A$:
$$A_z = \langle (i,j,k) \in \mathbb{Z}^3 : X(j,k)Y(k,i) = 1 \rangle , \\
A_x = \langle (i,j,k) \in \mathbb{Z}^3 : Y(k,i)Z(i,j) = 1 \rangle , \\
A_y = \langle (i,j,k) \in \mathbb{Z}^3 : Z(i,j)X(j,k) = 1 \rangle . $$
Then it returns
$A_z/A$,
$A_x/A$, and
$A_y/A$ as separate sets. In view outputs, elements of these sets get written to voxels in a simple
$\{R,G,B\}$ color space. The complement action is important because, depending on how Graphics3D stacks coincident blocks, a wrong color could possibly occur (example follows).
To simplify the situation, we can set say
$Y$ to monotone by choosing either
$Y(k,i)=0$ or
$Y(k,i)=1$ (over the entire domain) and see what happens.
xuanxue = "玄学";
bitmapBlank = Table[0, {i, 1, 14}, {j, 1, 14}];
bitmaps2 = With[{two =
RastToBitmap[Rasterize[#], 2] & /@ Characters[xuanxue]},
Join[Flatten[Append[two, #] & /@ {bitmapBlank, bitmapBlank + 1}, 1],
Flatten[Append[Reverse@two, #] & /@ {bitmapBlank, bitmapBlank + 1}, 1]]];
bitmaps2Ims = Image[Mod[# + 1, 2]] & /@ bitmaps2

BWTest = imDat[Partials[Sequence @@ #]] & /@ Partition[bitmaps2, 3];
TableForm /@ BWTest
Flatten[Superpose /@ BWTest]
CheckVals = MapThread[ImageSubtract,
{bitmaps2Ims, Flatten[Superpose /@ BWTest]}]
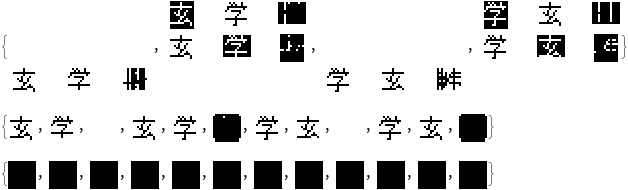
Great It worked! Except, oh wait a second, oh no!! The black check squares are hiding negative values that prove False results:
Partition[Mod[CheckVals, 2], 3]
So what happened? The bounding boxes of non-zero content do not match dimension from row to column, and this matters because they share an index diagonally. Notice that order of symbols matters, and for light on
$Y$, the second character turns out wrong, while for dark on
$Y$, both characters turn out fine.
Subtract @@ Reverse[MinMax[#]] & /@
Transpose[Position[bitmaps2[[1]], 1]]
Subtract @@ Reverse[MinMax[#]] & /@
MinMax /@ Transpose[Position[bitmaps2[[2]], 1]]
Out[] = {11,10}
Out[] = {11,10}
The clipping actually isn't that bad, and we still get relatively readable outputs, even in three dimesions. It's interesting to see what happens choosing light or dark:
Column[RGBResults[#] & /@ Partition[bitmaps2, 3]]

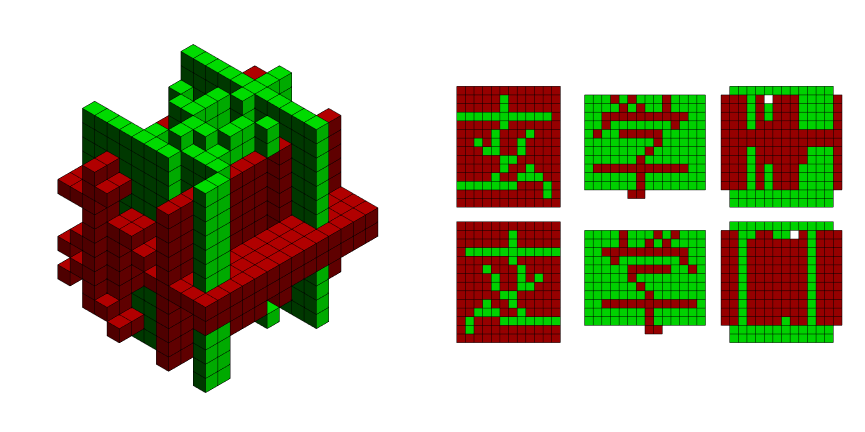


To reiterate, monotone Blue voxelgrams are almost readable, while Dark Red / Green voxelgrams totally readable. Anyone can explain why one graph is all Blue, while the other no Blue?
Anyways, no we know the secret, so it leads to an exploit and "further testing". If we make the bounding box very small, then we can slice out tiny segments and make the crypto (ha ha, joke) more difficult to read.
bitmapX = ReplacePart[
bitmapBlank, {{7, 7} -> 1, {8, 8} -> 1, {8, 7} -> 1, {7, 8} -> 1,
{6, 9} -> 1, {9, 6} -> 1, {6, 6} -> 1, {9, 9} -> 1}];
Exploit = {bitmaps2[[2]], bitmapX, bitmapBlank, bitmaps2[[2]],
bitmapBlank, bitmapX};
ExploitIm = Mod[Image[#] + 1, 2] & /@ Exploit
BWTest = imDat[Partials[Sequence @@ #]] & /@ Partition[Exploit, 3];
TableForm /@ BWTest;
Flatten[Superpose /@ BWTest]
Mod[MapThread[ImageSubtract, {ExploitIm, Flatten[Superpose /@ BWTest]}], 2]
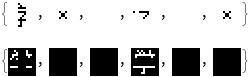
And in 3D:


These error cases are pretty convincing as to how a conditional could be written to gaurantee correct output. We need that sort of rigor before scheming about multi-million dollar autoglyph-style NFT business, possibly using some extra haskell programs. We definitely don't want multi-million dollar rounding errors!
Now the question of whether RGB face-first projection is equivalent to looking at Black and White Parts, Answer, seems yes, but maybe no. Say that we look along
$z$ at either
$Z(i,j)X(j,k)$ or
$Y(k,i)Z(i,j)$. Chose constant
$(i,j)=(a,b)$, if
$Z(a,b)$ is set, then we should scan along variable
$k$ and find some
$Y(k,a)=1$ with
$X(b,k)=0$ or some
$X(b,k)=1$ with
$Y(k,a)=0$, usually. A problem is if
$X$ and
$Y$ are transpose? Let's try one more test:
(at this point, functionalized test code needed?? )
bitmapSlash = ReplacePart[
Total[RotateRight[IdentityMatrix[14], #] & /@ {-1, 0, 1}], {{14,
1} -> 0, {1, 14} -> 0}];
Exploit2 = {Exploit[[1]], bitmapSlash, bitmapSlash};
Exploit2Im = Mod[Image[#] + 1, 2] & /@ Exploit2
BWTest = imDat[Partials[Sequence @@ #]] & /@ {Exploit2};
TableForm /@ BWTest
Flatten[Superpose /@ BWTest]
Mod[MapThread[ ImageSubtract, {Exploit2Im, Flatten[Superpose /@ BWTest]}], 2]
RGBResults[Exploit2]


But ah ha! We also need
$a=b$ chosen on diagonal, then the slash cut shows up, but it is in the Black / White data as desired. Whew, close call! Similarly if there is a natural absence, it should also occur in the Black / White data before RGB. What we can't predict easily is which correct color will show up where.
A few more counter cases, and the theorem will probably turn out clear as space.