
Above is the painting by Parmigiano "Self-portrait in a Convex Mirror". Based upon my past contribution on reflection and anamorphism in spherical mirrors, I investigated if I could make a similar "painting"using Mathematica. Here is the geometrical setup:
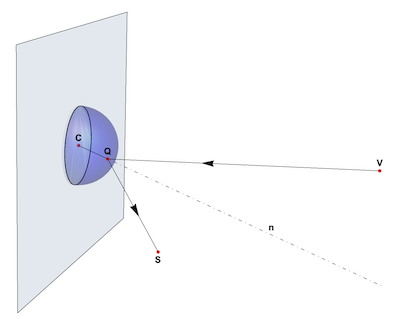
C is the center of he mirror sphere, V is the view point and let S be a point to be reflected. The first problem is to find a point Q on the sphere such that the light ray VQ and the reflected ray QS form equal angles with the normal n on the sphere at Q. I wrote a function including an NSolvevalues stating the laws of reflection: V,C, S and Q in same plane and vector angles VQ to n and SQ to n must be equal:
findIntersection[ptS : {xs_, ys_, zs_}, xv_] :=
Module[{ptC = {0, 0, 0}, plane, ptV = {xv, 0, 0}},
plane = InfinitePlane[{ptC, ptV, ptS}];
Quiet@First[
NSolveValues[{x, y, z} \[Element] Sphere[] &&
VectorAngle[ptV - {x, y, z}, {x, y, z}] ==
VectorAngle[ptS - {x, y, z}, {x, y, z}] && {x, y,
z} \[Element] plane && x > 0, {x, y, z}]]]
Works all right but the problem is the time it takes to find just one point Q. And I need a Q for every pixel in an image!
RepeatedTiming[findIntersection[{3.5, -4.5, -1.5}, 7.55]]
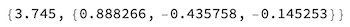
I know about the new compiler of the Wolfram Language but I am not familiar enough with it to write myself a CompiledFunction version of my function. The old Compile does not work properly for this and takes even longer:
findIntersectionCF = Compile[{{ptS, _Real, 1}, {xv, _Real}},
First@NSolveValues[{x, y, z} \[Element] Sphere[] &&
VectorAngle[ptV - {x, y, z}, {x, y, z}] ==
VectorAngle[ptS - {x, y, z}, {x, y, z}] && {x, y, z} \[Element]
InfinitePlane[{{0., 0., 0.}, {xv, 0., 0.}, ptS}] && x > 0, {x,
y, z}], CompilationTarget -> "C"]

My question is : Can somebody at Wolfram or this community convert my function to the new CompiledFunction code and speed my function up?