Hey there, I really @Armando Benjamín Cruz Hinojosa I like this, although I think we need more pie charts and word clouds and need to really show how to install the paclet, which really just means that all we need to do is have the file and install it. Actually, we can use the PacletInstall function to install the paclet and the rest is history.
PacletInstall["ArmandoCruz/ZeroKnowledgeProofs"];
Needs["ArmandoCruz`ZeroKnowledgeProofs`"]
zkProofHC = GenerateZeroKnowledgeProof["HamiltonianCycle"];
publicProblemHC = zkProofHC["ZeroKnowledgePublicProblem"];
privateSolutionHC = zkProofHC["ZeroKnowledgePrivateSolution"];
Row[{publicProblemHC["PublicProblem"],
Graph[privateSolutionHC["PrivateSolution"], VertexLabels -> "Name",
GraphLayout -> "CircularEmbedding"]}]
proverHC = GenerateZeroKnowledgeProver[privateSolutionHC, 5];
cipherHC = proverHC["ZeroKnowledgePrivateCipher"];
witnessHC = proverHC["ZeroKnowledgePublicWitness"];
cipherGraphs =
TableForm[
Transpose[
Table[{Graph[cipherHC["PrivateCipherSolutions"][[i, "Cipher"]],
VertexLabels -> "Name",
GraphLayout -> "CircularEmbedding"]}, {i,
Length[cipherHC["PrivateCipherSolutions"]]}]]]
solutionGraphs =
TableForm[
Transpose[
Table[{Graph[cipherHC["PrivateCipherSolutions"][[i, "Solution"]],
VertexLabels -> "Name",
GraphLayout -> "CircularEmbedding"]}, {i,
Length[cipherHC["PrivateCipherSolutions"]]}]]];
queryHC = GenerateZeroKnowledgeQuery[witnessHC];
queryHC["Queries"];
responseHC = GenerateZeroKnowledgeResponse[cipherHC, queryHC];
TableForm[
Transpose[
Table[{Graph[responseHC["Responses"][[n]], VertexLabels -> "Name",
GraphLayout -> "CircularEmbedding"]}, {n, 5}]]];
VerifyZeroKnowledgeProof[publicProblemHC, witnessHC, queryHC, \
responseHC]
ConnectGraphs[n_] :=
Module[{proverHC, cipherHC, witnessHC, graphList, combinedGraph,
newEdges, connectedGraph},
proverHC = GenerateZeroKnowledgeProver[privateSolutionHC, n];
cipherHC = proverHC["ZeroKnowledgePrivateCipher"];
witnessHC = proverHC["ZeroKnowledgePublicWitness"];
graphList = witnessHC["PublicCipherProblems"];
combinedGraph = GraphUnion @@ graphList;
newEdges =
Table[First[VertexList[graphList[[i]]]] \[UndirectedEdge]
First[VertexList[
graphList[[Mod[i + 1, Length[graphList], 1]]]]], {i,
Length[graphList]}];
connectedGraph = EdgeAdd[combinedGraph, newEdges];
Graph[connectedGraph, VertexLabels -> "Name",
GraphLayout -> "CircularEmbedding"]]
TableForm[Transpose[Table[{ConnectGraphs[n]}, {n, 5}]]]
Then we are actually able to show how to use the ZeroKnowledgeProofs packlet in the Wolfram Language. That's for Isomorphism, HamiltonianCycle, and SAT "problems" that all get summed up.
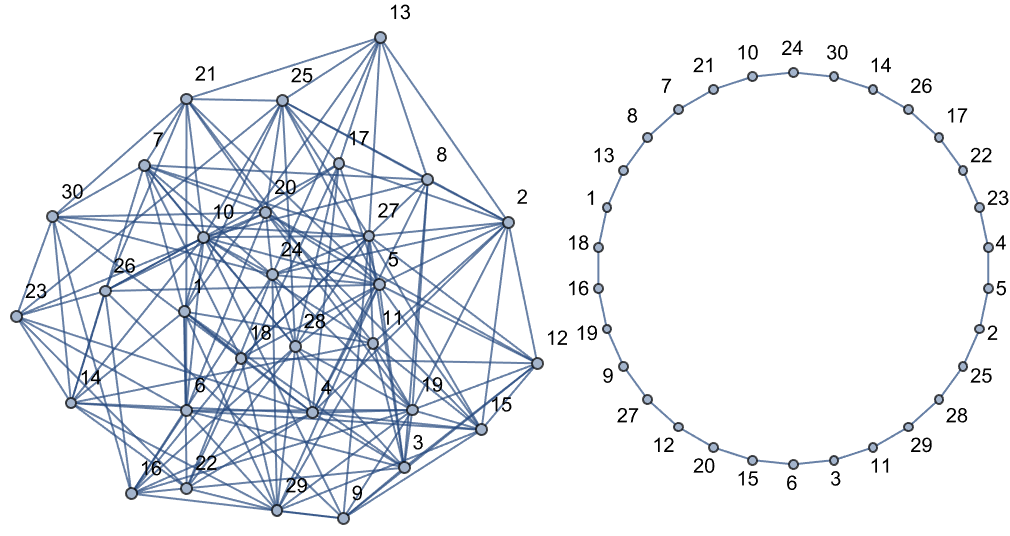
Wouldn't it be cool to solve the Boolean Satisfiability Problem, this is within the ArmandoCruz/ZeroKnowledgeProofs that makes it possible to solve public problems with private solutions and then verify them? The secret, hidden Hamiltonian Cycles in the Graph can be created and displayed.

Emphasize the graph structure side by side and use witnesses in the proof path, and then get some response for showing that we proved the visual queries, that is True, and the next is True. This really made my day I enjoyed every proof in here.

We know that the computations are being executed correctly without actually executing them!
There's no man in the middle there's just knowledge that there's a solution, and yeah there's the NP-complete 3SAT and Quadratic Span Problem compilers and @Armando Benjamín Cruz Hinojosa it's the interactivity of your proof protocols and the smaller witness sizes and shorter verification times and the generation of computationally hard problems & solutions, they have significant implications for non-interactive, privacy in decentralized technology.