@Theodore Mollano generalize this it's like the thing that you do with the graph tilings.

My favorite function of all time is the token event graph like @Richard Charette. I used to like the token event graph.

graph = CompleteGraph[65,
   VertexLabels -> Placed["Name", Center],
   EdgeStyle -> 
    Thread[EdgeList[graph] -> 
      ColorData["SunsetColors"] /@ Rescale[Range[EdgeCount[graph]]]],
   VertexSize -> 0];
highlightedGraph = SetProperty[
   graph,
   {EdgeStyle -> Thread[
      RandomSample[EdgeList[graph], Floor[EdgeCount[graph]/100]] -> 
       Directive[Thick, Lighter[Pink]]
      ]}];
tokenEventGraph = ResourceFunction[
    ResourceObject[<|"Name" -> "TwoWayStringTokenEventGraph",
      "UUID" -> "6efe33fc-c0fa-4d4f-8198-1e9db29ac03e",
      "ResourceType" -> "Function", 
      "ResourceLocations" -> {CloudObject[
         "https://www.wolframcloud.com/obj/wolframphysics/Resources/\
6ef/6efe33fc-c0fa-4d4f-8198-1e9db29ac03e"]}, "Version" -> None,
      "DocumentationLink" -> 
       URL["https://www.wolframcloud.com/obj/wolframphysics/\
TwoWayStringTokenEventGraph"],
      "ExampleNotebookData" -> Automatic, 
      "FunctionLocation" -> 
       CloudObject[
        "https://www.wolframcloud.com/obj/wolframphysics/Resources/\
6ef/6efe33fc-c0fa-4d4f-8198-1e9db29ac03e/download/DefinitionData"], 
      "ShortName" -> "TwoWayStringTokenEventGraph",
      "SymbolName" -> 
       "FunctionRepository`$6efe33fcc0fa4d4f81981e9db29ac03e`\
TwoWayStringTokenEventGraph"|>]][
   Thread[UndirectedEdge @@@ EdgeList[graph] -> StringJoin[
      RandomChoice[{"Dreamy", "Sunset", "Honey", "Melody", 
        "Butterfly"}, 2]]],
   "Sorting" -> True,
   VertexSize -> .75,
   Sequence["EventDeduplication" -> True,
    "TokenLabeling" -> False]];
HighlightGraph[highlightedGraph, tokenEventGraph]

My favorite function is Map[].

Okay so there's these tilings and then, @Theodore Mollano when you walk in it is like heaven and Earth. I always wondered how to make 3d token event graphs.

@Theodore Mollano I see your article exploring the graph tilings, and the constrained network systems. It almost makes me want to use Graph3D, to separate different evolution paths in 3D space.

Graph[GraphUnion @@ generateSimpleTemplate[{3}, 6], 
 VertexStyle -> RandomColor[RGBColor[1, 0.51, 0.2]], 
 EdgeStyle -> RGBColor[0.331, 0.4884, 0.7223]]

With @James Boyd this is easy. There's an old Ruliad proverb that whenever you're working with big graphs, when you're dancing with the Ruliad you should bitmap.

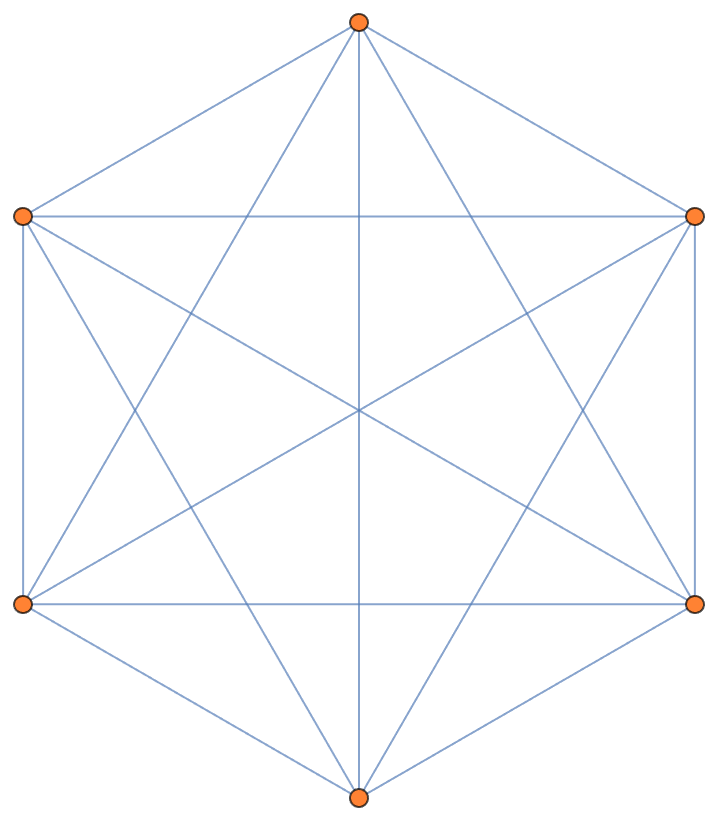
Because graph tilings have important relations to Combinatorics, Graph Theory, and Computer science, and this article was Space & Time.

With[{graphstwo = 
   Select[DeleteDuplicates[
     Graph[VertexList@#, #, 
        VertexStyle -> {RandomColor[], EdgeForm[Black], 
          AbsolutePointSize[15]}, 
        EdgeStyle -> {RandomColor[], AbsoluteThickness[2.5]}] & /@ 
      Subsets[EdgeList[
        GraphUnion[CompleteGraph[5], 
         Graph[{1 \[UndirectedEdge] 1, 2 \[UndirectedEdge] 2, 
           3 \[UndirectedEdge] 3, 4 \[UndirectedEdge] 4, 
           5 \[UndirectedEdge] 5}]]]], IsomorphicGraphQ], 
    ConnectedGraphQ]}, 
 Grid[Partition[graphstwo, 50], Frame -> None, 
  ItemSize -> {1.5, 1.5}]]

Offer us a glimpse into statistical and algorithmic connections, and we have got the template tiling.

These are illustrative examples of the k-valent tilings.

Grid[Partition[
  Flatten[Map[Map[NeighborhoodGraph[#, 1, 1] &, #] &, 
    Map[{doubleEdge[#], tripleEdge[#], tripleEdge[doubleEdge[#]]} &, 
     graphstwo], {2}]], 50], Frame -> None, ItemSize -> {1.5, 1.5}]

And the @Stephen Wolfram future problem determines the largest graph that can be formed using a simple set of templates.

This is such a good framework for project culmination.