But in general, just as there are many different expressional forms of resource allocation there is a definite procedure..as soon as you have π and that phenomenon of using Mathematica for implementing the algorithm and visualizing the results really bites you in the sense of the resource allocation problem in Lagos. The idea is that we only use weights for use cases where we don't have full control of the loaded greedy algorithm which we include to compute the optimal allocation of resources. So we have got to look at the constraints such as the total weight and the project interdependencies. If I look at it and model it (and don't sneeze because the project interdependencies are quite fragile in the sense of practice)..I have got to just, under-stand the visualization of the Mathematica's computational and graphical tools, by using these kind of industrial strength methods and so on. Once you guess the answer, you can always differentiate; if you know the form that that answer is supposed to have, and you differentiate that answer again and then solve that equation for what values of a, b, and c you have so that that derivative is actually the thing you started with so that method, is one that one uses all the time when one tries to get computers and isn't just using these industrial strength formulas. You just have to match up those coefficients and so on; the goal is to minimize the total cost and so forth of purchasing lumber wherein the same amount of lumber can have multiple meanings in the list of cuts and we fulfill this, there's, to some extent this analogous cost of making sure that the sum of cuts made from the available boards can meet or exceed the demand specified in the cut-list. It's not quite the same thing as the knapsack problem (and the cat's already out of the bag with regard to that problem) because we have this minimization problem and we can, use "it" to Minimize..specifically, the Minimize function "utilizes" integer constraints for board counts.
lumberCutManagementList = {33.5, 25.75, 12, 16, 16, 16.5, 33.5, 64.5,
90.25, 90.5, 90.5, 64, 64, 64};
lumberList = {{8*12, 5.68}, {10*12, 8.84}, {12*12, 10.62}, {14*12,
12.36}, {16*12, 14.15}};
availableLengths = lumberList[[All, 1]];
costs = lumberList[[All, 2]];
variables = Array[x, Length[availableLengths]];
totalCost = costs . variables;
constraints =
Table[Total[Floor[availableLengths/length]*variables] >=
Count[lumberCutManagementList, length], {length,
Union[lumberCutManagementList]}];
solution =
Minimize[{totalCost, constraints,
variables >= 0 && Element[variables, Integers]}, variables];
numBoards =
Table[{availableLengths[[i]], variables[[i]] /. solution[[2]]}, {i,
Length[availableLengths]}];
totalCostFinal =
Total[Table[(variables[[i]] /. solution[[2]])*costs[[i]], {i,
Length[availableLengths]}]];
numBoards
totalCostFinal
cuttingPlan = {{192, lumberCutManagementList}};
visualizeCuttingPlan[availableLengths_, cutList_, cuttingPlan_] :=
Module[{cuts, colors, rectangles, cutLabels, boardGraphics,
boardLabels}, colors = RandomColor[Length[cutList]];
boardGraphics =
Table[cuts = cuttingPlan[[i, 2]];
Module[{x = 0, rects = {}, labels = {}},
Do[AppendTo[
rects, {colors[[Position[cutList, cut][[1, 1]]]],
Rectangle[{x, i}, {x + cut, i + 1}]}];
AppendTo[labels,
Text[Style[ToString[cut] <> " in", FontSize -> 10], {x + cut/2,
i + 0.5}]];
x += cut;, {cut, cuts}];
{rects, labels}], {i, Length[cuttingPlan]}];
rectangles = Flatten[boardGraphics[[All, 1]], 1];
cutLabels = Flatten[boardGraphics[[All, 2]], 1];
boardLabels =
Table[Text[
Style[ToString[cuttingPlan[[i, 1]]] <> " in", FontSize -> 12,
Bold], {-10, i + 0.5}], {i, Length[cuttingPlan]}];
Graphics[{boardLabels, rectangles, cutLabels},
ImageSize -> {1000, 300},
PlotRange -> {{-20, Max[availableLengths]}, {0,
Length[cuttingPlan] + 1}}, AspectRatio -> 0.3,
PlotRangePadding -> Scaled[0.1], Axes -> True,
AxesLabel -> {"Length (inches)", "Board Number"},
Ticks -> {Automatic, Range[Length[cuttingPlan]]}]]
visualizeCuttingPlan[availableLengths, lumberCutManagementList, \
cuttingPlan]
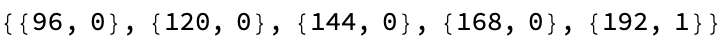
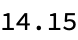
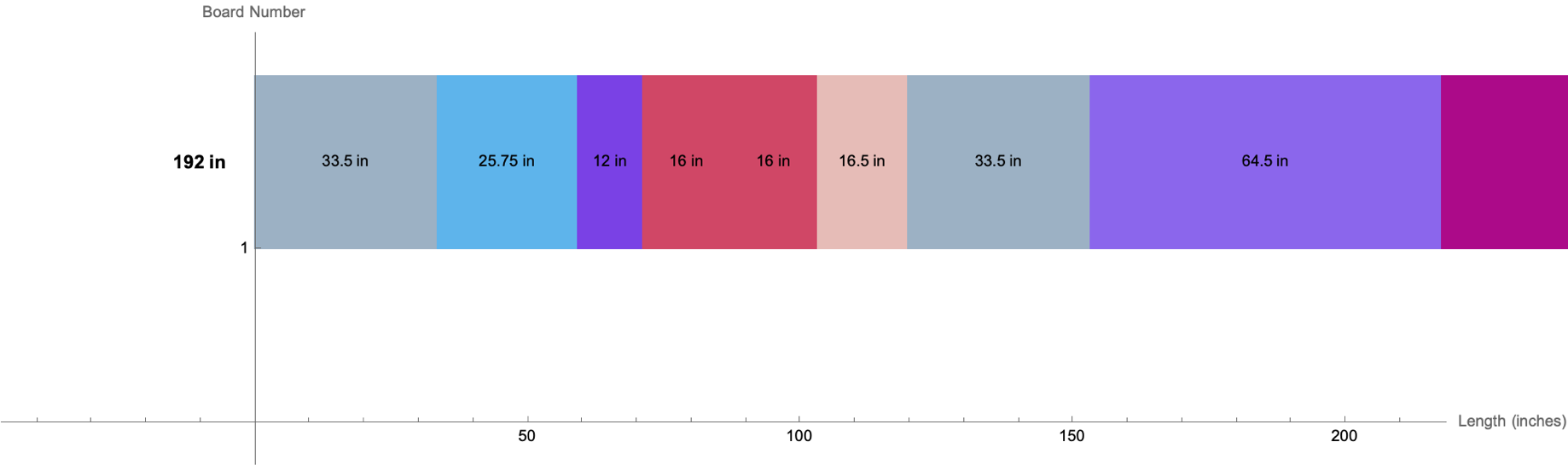
And things get thoroughly wrong but "still" the solution does minimize cost while meeting the cuts that are required. It's the computation calculation that provides an intuitive view, we can collapse and then fulfill the total cost quite "reasonably" it's quite breath-taking. There's an ancient Rulial story about a statue two vast and trunkless legs of stone, the Lagos district of the crumbled empire, your article @David Daniel was like hitching a ride on the spacecraft.
benefits = {7, 9, 5, 8, 6, 5};
weights = {3, 4, 1, 3, 5, 2};
vars = Table[Subscript[x, s], {s, 6}];
obj = benefits . vars;
constr1 = weights . vars <= 10;
constr2 = Subscript[x, 1] + Subscript[x, 2] <= 1;
constr3 = Subscript[x, 1] + Subscript[x, 6] <= 1;
constr4 = Subscript[x, 2] + Subscript[x, 3] <= 1;
constr5 = Subscript[x, 3] + Subscript[x, 4] <= 1;
constr6 = Subscript[x, 3] + Subscript[x, 6] <= 1;
constr7 = Subscript[x, 4] + Subscript[x, 5] <= 1;
constr8 = Subscript[x, 5] + Subscript[x, 6] <= 1;
intervals = Thread[0 <= vars <= 1];
{val, point} =
Maximize[{obj, constr1, constr2, constr3, constr4, constr5, constr6,
constr7, constr8, intervals}, vars, Integers]
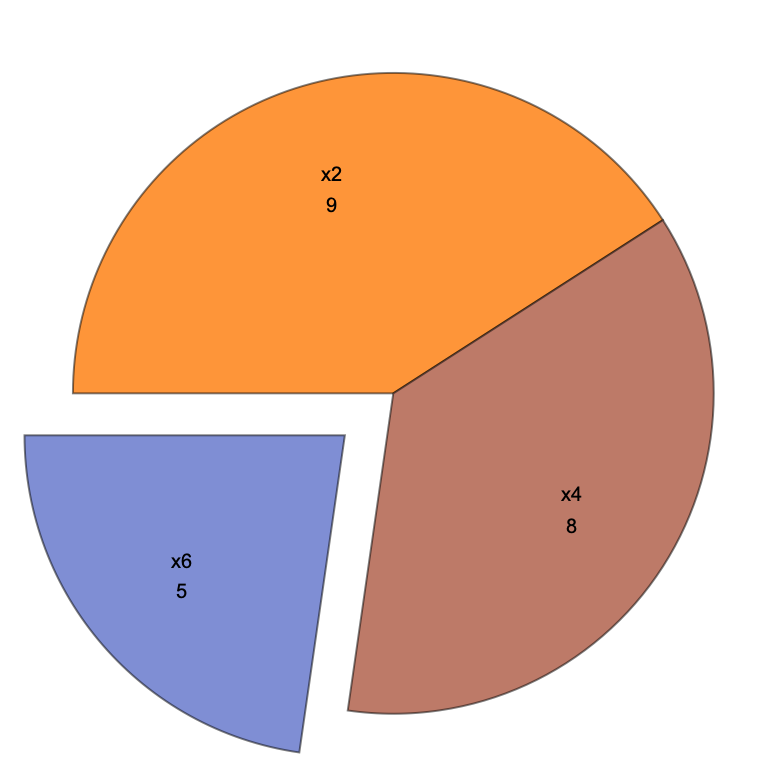
benefitsValues = benefits*Values[point];
PieChart[benefitsValues,
ChartLabels ->
Table[Labeled["x" <> ToString[i], benefitsValues[[i]]], {i,
Length[benefitsValues]}]]
And I was crying when I heard about the Ruliad because it's just phenomenal like this beautiful graph that we have here solving the Project Allocation Problem (PAP) using the Fractional Knapsack model.
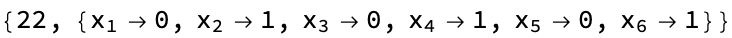
The objective is to maximize the benefit of a set of six projects, and we can do more.
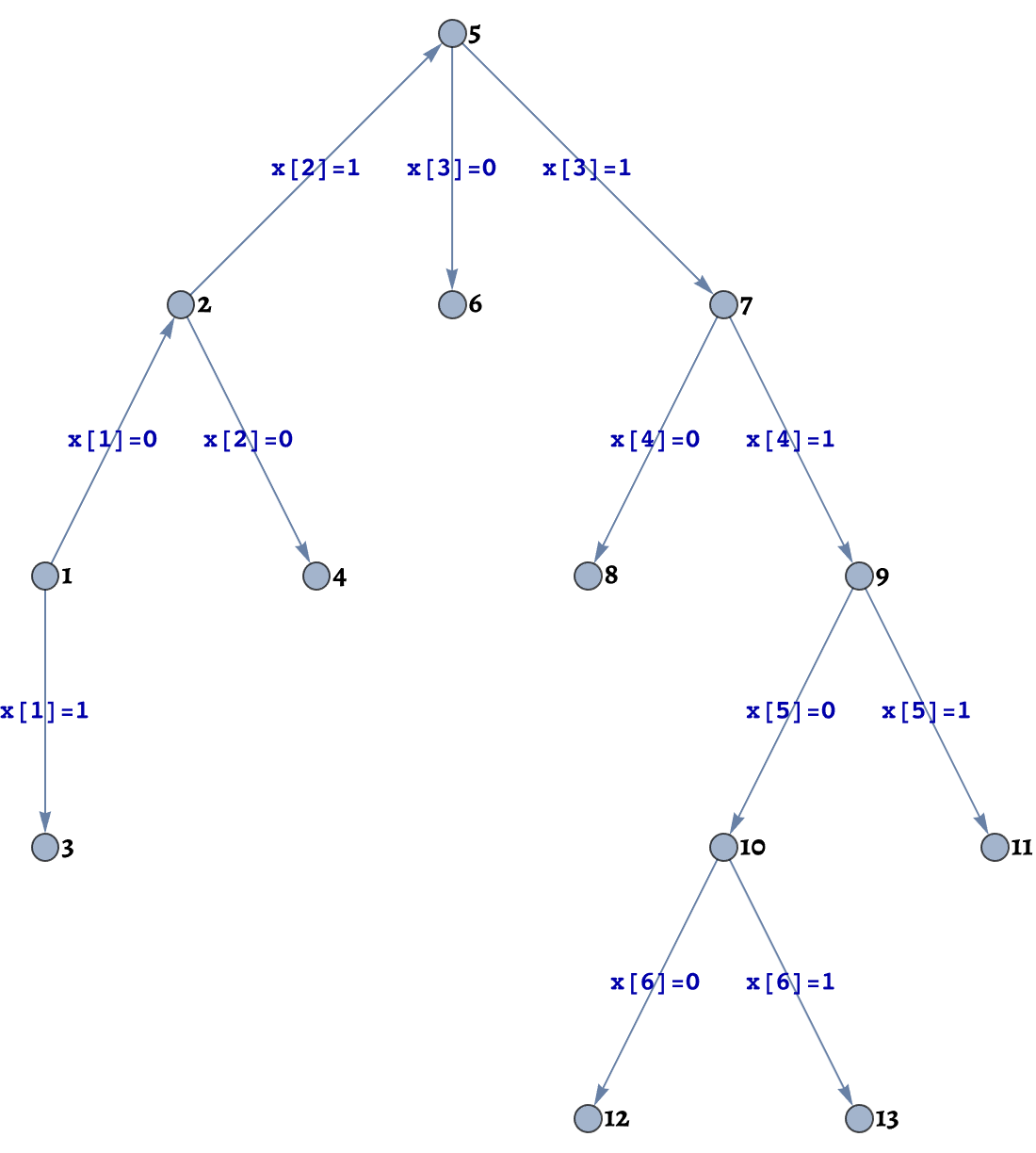
edges = {Labeled[1 -> 2, "x[1]=0"],
Labeled[1 -> 3, "x[1]=1"],
Labeled[2 -> 4, "x[2]=0"],
Labeled[2 -> 5, "x[2]=1"],
Labeled[5 -> 6, "x[3]=0"],
Labeled[5 -> 7, "x[3]=1"],
Labeled[7 -> 8, "x[4]=0"],
Labeled[7 -> 9, "x[4]=1"],
Labeled[9 -> 10, "x[5]=0"],
Labeled[9 -> 11, "x[5]=1"],
Labeled[10 -> 12, "x[6]=0"],
Labeled[10 -> 13, "x[6]=1"]};
Graph[edges,
GraphLayout -> "LayeredEmbedding",
VertexLabels -> Placed["Name", After],
VertexSize -> 0.1,
VertexLabelStyle ->
Directive[FontFamily -> "Alegreya SC", Bold, 16],
EdgeLabelStyle ->
Directive[FontFamily -> "Courier", Bold, 14, Darker[Blue]]
]
And what do you say about the greedy algorithm? Even if we do its bidding, it's amazing because we can make optimal project selections.
Thank you @David Daniel for publishing this version. It's like the way that something would be written today, the cultural difference, that something was put here on purpose, the 0-1 Knapsack problem, a variation of the knapsack problem where each item can be included only once or not at all. We're keeping within the knapsack's capacity so it doesn't weigh that much but it has so many benefits and values.
ClearAll[FractionalKnapsack]
SortByRatio[weights_,
profits_] := {weights, profits}[[All,
Ordering[N[profits/weights], All, Greater]]]
FractionalKnapsack[noOfObjects_, weightsAndprofits_, capacityOfbag_] :=
Module[{x, tp, i, u, weight, profit}, {weight, profit} =
SortByRatio @@ Transpose[weightsAndprofits];
x = ConstantArray[0.0, noOfObjects]; tp = 0; u = capacityOfbag;
For[i = 1, i <= noOfObjects && weight[[i]] <= u, i++, x[[i]] = 1.0;
tp += profit[[i]]; u -= weight[[i]]];
If[i <= noOfObjects, x[[i]] = u/weight[[i]];
tp += x[[i]]*profit[[i]]];
Labeled[BarChart[x, ChartStyle -> 24],
Style["Your Maximum Profit is " <> ToString[N@tp]]]]
weightsAndProfits =
Transpose[{RandomInteger[{1, 20}, numItems = 20],
RandomInteger[{5, 50}, numItems = 20]}];
FractionalKnapsack[numItems, weightsAndProfits, capacity = 50]
@David Daniel the "problem" of indiscriminate allocation of projects by decision-makers, well, it turns out that this graph is actually a beautiful graph for one day, and guess what? The cards are down, and the [WSS22] Fractional Knapsack model for project allocation problem is the physical embodiment of these cards in that the proposed Fractional Knapsack model is completed with efficiency and we can see each aspect of the allocated budget.
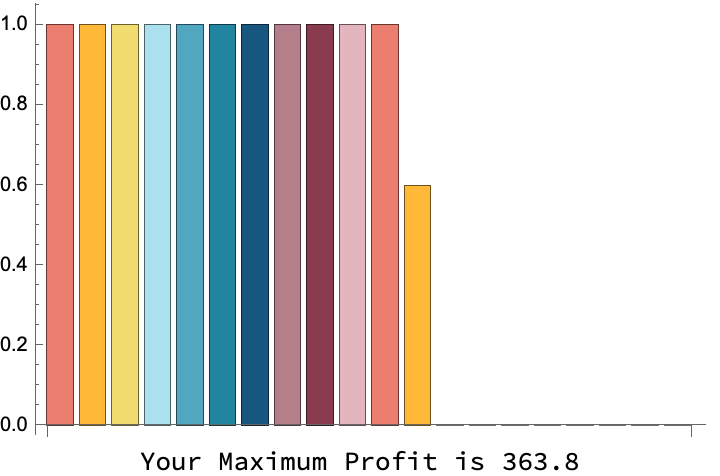
The algorithm can be applied to project management problems and we should eagerly be supportive of its inundation, because any amount can guide us through this project like we can @David Daniel with this fantastic adoption of the Fractional Knapsack Algorithm.
I want to say which atom is at that particular position and you know the world is made of atoms, because there are only a discrete set of positions at which there is an atom. This idea of infinitesimal distances all over the place isn't going to make sense because there is an elementary length, it might be 10^{-n} meters but there is an elementary length.
logLength = 40;
lengthList = {8, 12, 16, 20};
quantity = {90, 111, 55, 30};
costs = {5, 7, 10, 12};
nLengths = Length[lengthList];
patterns = DiagonalMatrix[Floor[logLength/# & /@ lengthList]];
nPatterns = Length[patterns[[1]]];
x = Array[x, nPatterns];
infraSolution =
LinearProgramming[ConstantArray[1, nPatterns], Transpose[patterns],
quantity, Table[0, {nPatterns}]];
logsUsed = Total[infraSolution];
Print["Initial solution uses ", logsUsed, " logs"];
generateNewPattern[lambda_] :=
Module[{subProblem, newPattern, cuts = Array[cuts, nLengths]},
newPattern =
NMinimize[{1 - lambda . cuts,
Total[lengthList cuts] <= logLength && cuts >= 0}, cuts];
newPattern[[2]]];
reducedCost = -Infinity;
exitflag = True;
patternsUpdated = patterns;
While[reducedCost < -0.0001 && exitflag,
infraSolution =
LinearProgramming[ConstantArray[1, Length[patternsUpdated[[1]]]],
Transpose[patternsUpdated], quantity,
Table[0, {Length[patternsUpdated[[1]]]}]];
logsUsed = Total[infraSolution];
lambda = infraSolution;
newPattern = generateNewPattern[lambda];
reducedCost = 1 - lambda . newPattern;
If[reducedCost < -0.0001,
patternsUpdated = Append[patternsUpdated, newPattern];
Print["New pattern added, logs used: ", logsUsed],
exitflag = False];];
Print["Final solution uses ", logsUsed, " logs"];
totalWaste =
Total[Table[
Max[0, logLength - Total[lengthList*patternsUpdated[[i]]]], {i, 1,
Length[patternsUpdated]}]];
Print["Total waste: ", totalWaste, " feet"];
TableForm[
Transpose[{lengthList, quantity, patternsUpdated . infraSolution}],
TableHeadings -> {{"Length", "Required", "Produced"}}]
logsUsedByLength =
Table[Total[patternsUpdated[[All, i]]*infraSolution], {i, 1,
nLengths}];
TableForm[Transpose[{lengthList, logsUsedByLength}],
TableHeadings -> {{"Length", "Logs Used"}}]



And our Wolfram Educational Unit, you can actually get the physical book now and that's making use of all of the technology that shows how when you allow-list you're doing the needful, you're defining the variable cuts across space-time with a valid domain that is the Integers or the Reals or and some other direction that we can take but we know that that's sort of a vacuous statement in and of it-self. Rest assured that when we specify the domain with utmost desperation and dedication we can compatabilize the domain constraints and that's the reason why that our infinite loops in While, they start out but there's no conclusion they just trail off and that's what we do we "think so much" about the optimization of, multiplying numbers together and it's pretty easy to do but if you want to factor those numbers to figure out what numbers you could multiply together, that's prime time for knowing how to go back to the clear representation of resource allocation and reduce expenses in purchasing raw materials, that's a "formidable opponent". It turns out that as is often the case, with computations with integers when you're just multiplying and factoring and so on those turn out to be fundamentally "harder" to get a computer to do but it is something, that once you've taught a computer to do it it is "probably" easier because there are some pieces I don't know, than multiplying integers..harder to do that factoring than to do these integrals where I'm taking an integral and want to go back to where I'm starting from. That's the "combination of" computational efficiency with the "visualization" that serves as the foundation of creativity. In this system and Wolfram Institution of recursion we know that we can say hey, we can provide an intuitive view of how cuts are allocated across boards and thus make sure that all the cuts are assigned.