So I have been working some time on a very specific model called the Space Element Reduction Duplication (SERD) model that is similar to the wolfram model in the sense that it involves the evolution of a graph data structure space-time representation through discrete time evolving via update operations on the elements of the graph structure. The order of update operations can alter the outgoing state at each time-step and in this sense it generates causal and branchial graphs, and is very much as described in NKS a multi-way system. It has a few differences to the wolfram model. 1. Information (in the form of integers, arrays, or arrays of arrays) is stored on the nodes (gaps between elements) of the system. 2. Information is transferred between nearest neighbours through time and updated on point particles (the observers of the system). 3. Coordinates of particles are determined through a strain/curvature minimizing algorithms that fits particles in space and that are applied at each successive time step. There maybe some level of isomorphism to the wolfram model that I would be keen to discuss with member of this community however I have struggled to model this system using the wolfram model framework since I cannot seem to be able to enforce specific update operations through time, and accounting for the information propagation mechanisms has proven, for me at least, difficult to do. Never the less much of my research, as can be seen in my previous Mathematica notebook, which I have shared in a previous post https://community.wolfram.com/groups/-/m/t/2589079 has used Mathematica extensively to probe the behaviour of this system. My code tends to use Monte Carlo simulations and Multi-Leveled Monte Carlo Simulations (these behave like a series of consecutive Monte Carlo simulations where the outputs that satisfy given conditions are used as inputs for the next simulation recursively, this can have the effect of symmetry breaking, generating complexity and collapsing the set of states like an observation of the system) to observe expectation values of the evolution of position of particles and behaviour of substructures of the system, but inso doing I do lose information of the causal relationships between specific update events that the Wolfram Model is incredibly capable of doing and as a result my current code structure does not have the power to probe more quantum mechanical behaviour such as superposition and the uncertainty relations. I hope to make greater use of the Wolfram model in future to do this.
To give a brief overview, the system is a network with two fundamental elements, Point Particles (PPs) and Space Elements (SEs). The SEs form long strings of connected SEs that spatially separate PPs called interaction edges (IEs). SEs may do nothing, duplicate (1->2) or reduce (1->0) through one time step and PPs can do nothing, split (becoming 2 PPs separated by one SE) or merge (all SEs between them reduce and the two PPs become one PP, this can lead to internal structures of PPs in a compactified space that I wish to explore more in the future). When a split occurs it creates Propagating Structural Bifurcations (PSBs) along all incident IEs, these traverse the IEs at a rate of 1 SE per TS (demonstrated in my previous post https://community.wolfram.com/groups/-/m/t/2589090) and can overlap, cross but never overtake each other, causing a time delay to when splits may be observed by PPs. When mergers occur it can lead to multi-IEs and self-loop-IEs, or possibly 're-zipping of IEs' so there is likely a time delay from when mergers are observed. When duplications or reductions occur it adds to the information on the gaps surrounding the SE that duplicated or reduced (+1 for duplications and -1 for reductions) and that information then propagates through the IEs through time, leading to a time delay to when a reduction or duplication is observed. This information forms propagating information packets (PIPs) which behave similar to photons in that they can superpose, they transport quanta of energy/information at light speed and there is no limit to how many PIPs can be in any unit of space (unlike PPs which make up the matter particles and cannot exist in the same location if separated by at least one IE). Every PP has an 'awareness' of the state around it purely defined by the sum history of information that has been updated on it, in this sense matter has a 'reference frame' and acts as the observers of the system. This means that there is a hidden state and an observed state, (I have found it difficult to represent this within the Wolfram Model framework). In this sense it forms a multi-way system, the only true reality being the reality that is observed. Mass density is defined as the amount of PPs in a given space, energy density is defined as the amount of information in a given space. Most importantly this system emerges out of a philosophical consideration relating to the existence of planes of dimension within nothingness discussed in previous posts.
If this system were the universe then photons would travel along IEs through space to reach us. My latest paper looks at the growth rates of these IEs (since they are related to the overall growth rate of the system) and shows that when the hidden scale of the system is enforced to expand faster than the information propagation speed then the observed scale is constrained to be no more than the time information takes to travel across the system times the speed of light (which in this case is just 1), in other words a Hubble horizon. (There is a link here I strongly believe with light-cone dynamics of massive particles.)
There are then anthropic arguments as to how order emerges out of this seemingly chaotic system through selective observations, however this paper shows that in the case where the system expands exponentially/superluminally fast each PP is constrained to only observe a finite region of that space defined by the information propagation speed. It is then possible that the dark energy that is causing the accelerated expansion of space may be the information of the inflation that has not been observed reaching us at a later time. Furthermore, this expansion will result in addition duplications that will reduce the overall magnitude of reduction PIPs/photons, effectively reducing the energy, causing a ‘redshift’ of the PIPs/photons.
I've included some results if people are interested.
I will continue investigating this system for further physically comparable behaviour.
Firstly the emergence of photon-like information packets out of the IE system. The diagram below was created using Mathematica array plot. The blue dots correspond to negative numbers (reduction PIPs) and the orange represent smaller positive numbers (duplication PIPs). As you can see there are many background duplication PIPs, could this correspond to what is observed as dark energy if the universe has already been enforced to expand at much greater distances then we observe then there will be a surplus of duplication PIPs to reduction PIPs?
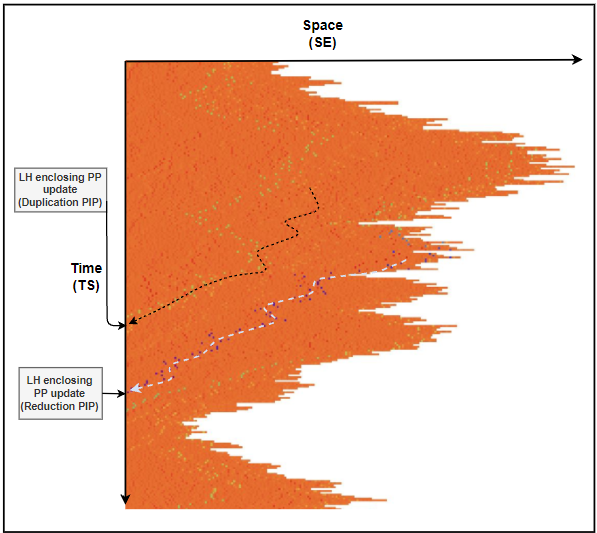
The graph below, created using Mathematica, shows how the observed state of IE evolves for one branch of the multi-way system. Notice the downward jumps. It's these constrictive jumps that correspond to the update of the PIPs/photons (in the full system, not just the single IE system, PIPs contain information of the entire state graph not just reductions from the IE that they are propagating along and so may result in repulsive responses as well as attractive ones). The gradual increase I see as having a relation to dark energy, resulting from the expansion of the universe that has already happened that we don't see and fills the background of all space. 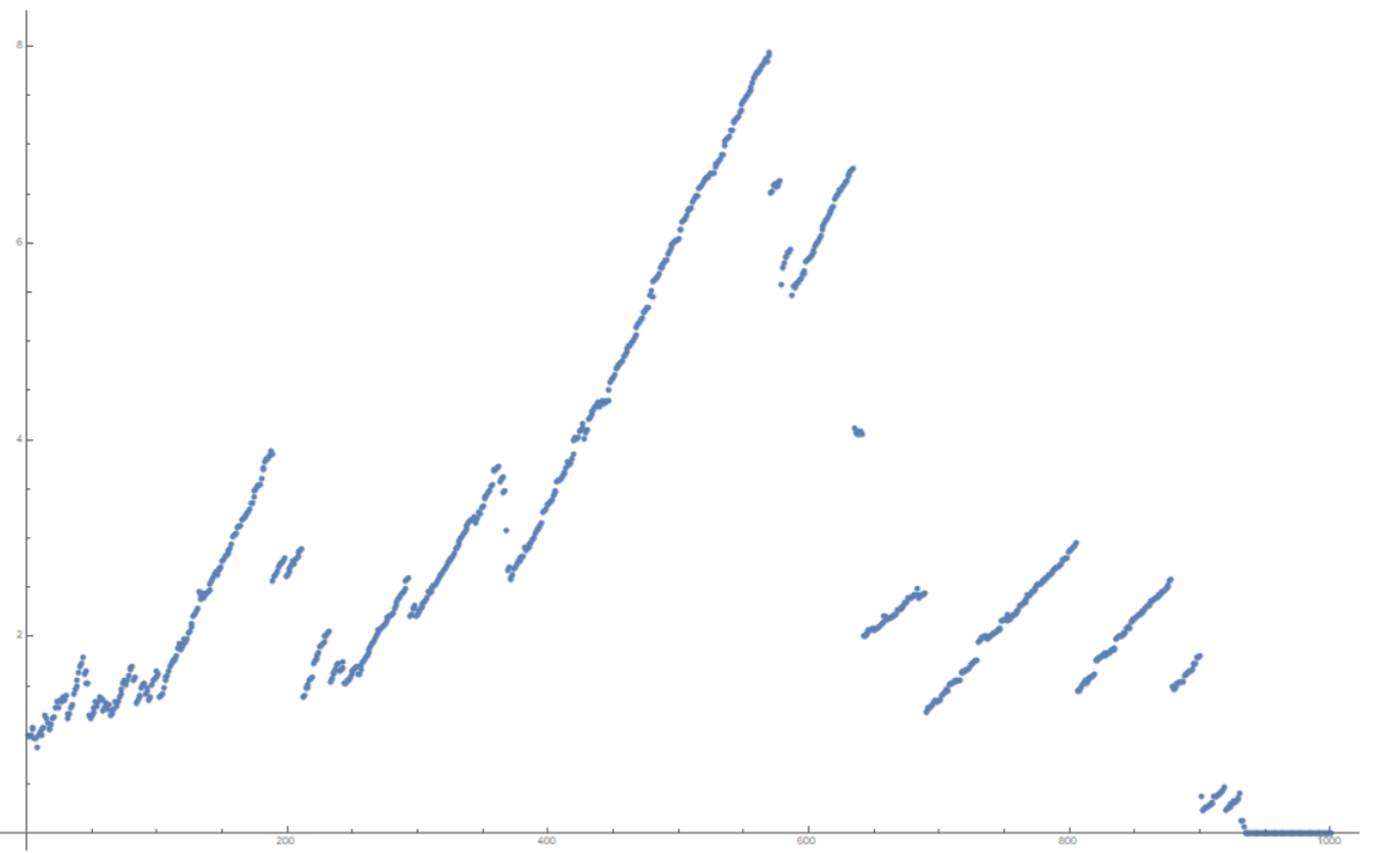
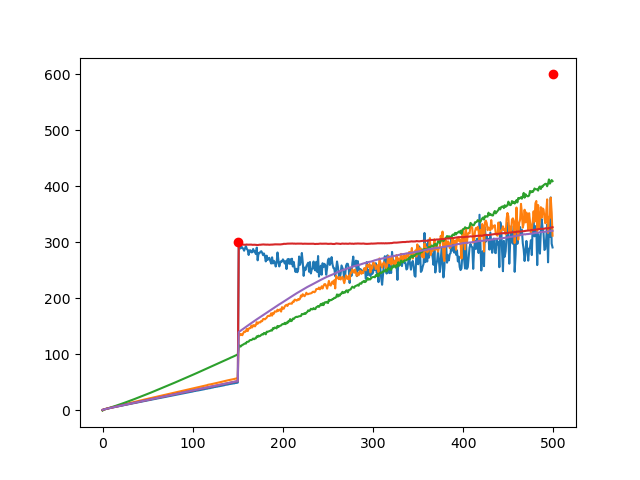
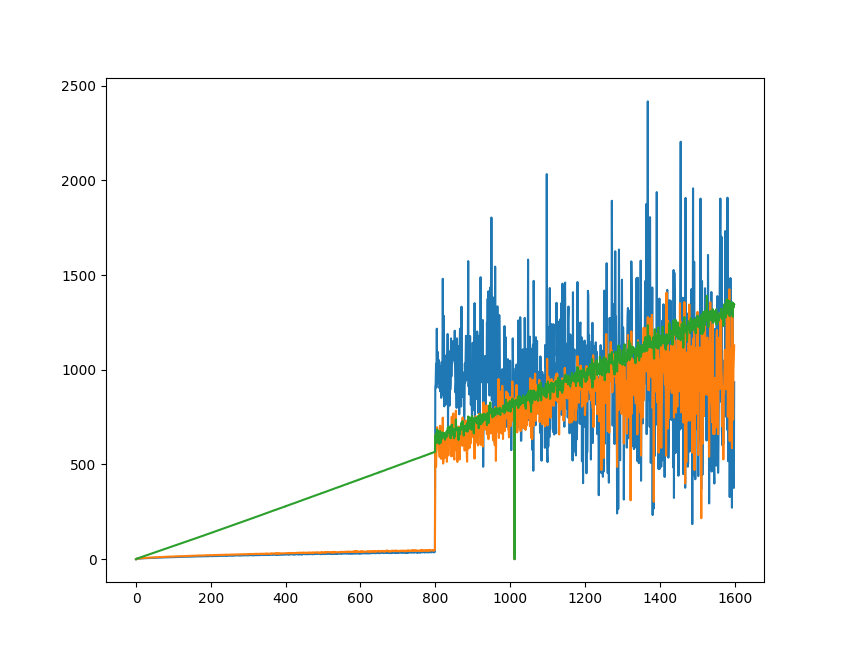
The growth rates of both the hidden scale (blue) at the instance of information observation and the observed scale (orange) at the instance of information observation, average information update time (green) at the instance of information observation, overall average hidden scale (red), overall average observed scale (purple). The red dot is the middle value of the range of hidden scales that the system is enforced to take at that time. This is what enforces the system to grow at a superluminal rate, however this enforcement could be argued for with an anthropic argument, or may occur naturally as described below.
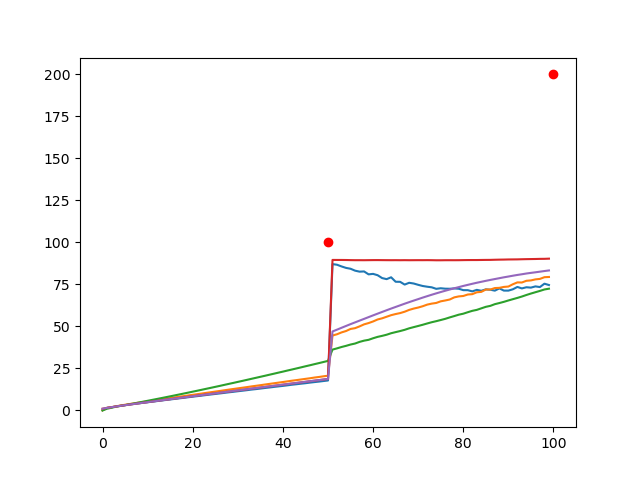
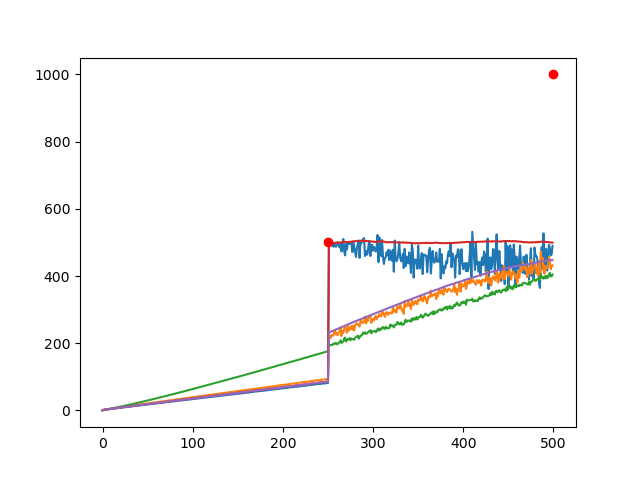
Notice here that as the system relaxes the hidden scale approaches the observed scale yet the system appears to continue to grow. I believe this to be down to the fact that IEs that don't fully reduce tend to grow larger (a sort of natural selection of Ies) as the IEs that shrink are more likely to fully reduce. This may lead to an overall growth rate of the system that I do not have the efficiency of simulation nor the computing power yet to fully explore.
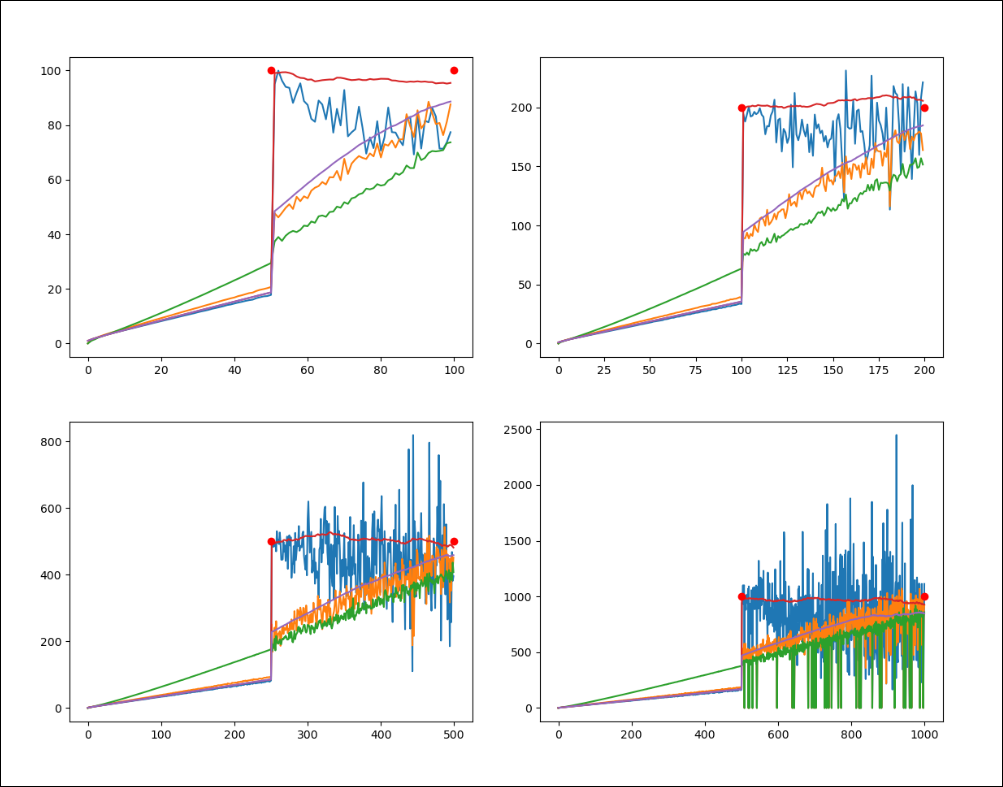
There is time dilation on receding point particle systems and it is possible still to see light from particles that are now receding away from us at superluminal velocities. If the universe inflates in an anthropic manner this will then lead to emergent causally bounded 'packet universes' each with their own horizons emerging out of this system.
I'm interested to hear peoples thoughts on these results and how they may relate to the observations made by the wolfram model, and physical observations in astronomy. Is there scope for this system to match up with physical observation?
Please feel free to reach out for any further discussions on this system, my work is very independent and I'm looking for collaboration on this project if people are interested. I'm also welcoming any information that may falsify the physical comparisons i make regarding this system.
Once my paper is published I may post it on here.
tommyleonwood@gmail.com https://twitter.com/TommyWo24564630
Connections to earlier posts:
https://community.wolfram.com/groups/-/m/t/2589079
https://community.wolfram.com/groups/-/m/t/2589090