Back in 1972, Salvador Dalí published five lithographs assembled in the suite "Anamorphoses". According to one of the galleries selling the prints: "when one of these prints is placed flat on a table with a cylindrical mirror about 3 inches in diameter at a specific spot a new image appears in the cylinder". This describes exactly the effect of "cylindrical anamorphosis", an optical illusion frequently used by Dalí to conceal "secret" or "forbidden" images in plain sight. I have been analysing anamorphosis here and here in previous community contributions.

Above is the complete set of prints (top row) and the reflections in a cylindrical mirror (bottom row). To the left is the "double image" I analysed here some time ago in this community. This time, I take a look at the skull (Le crâne) and see what I can do with the Mathematica functions I used.
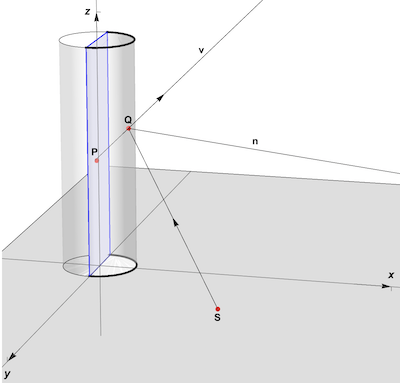
A point S in the x-y plane is observed as as P along the view line v. P is the reflection of S and S is the anamorphic map of P. The points S and P is form an enantiomorph pair. In my Wolfram Demonstration Cylindrical Mirror Anamorphosis, I showed how the function cylindAnamorphic below computes the coordinates of S from the coordinates of a reflected point P and the view direction phi formed by the view line v:
cylindAnamorphic[imagePnt : {yi_, zi_}, viewDir : phi_] :=
Module[{qx, qy,
qz}, {qx, qy, qz} = {yi, Sqrt[1 - yi^2],
zi - Sqrt[1 - yi^2] Tan[-phi]};
{(qx (2 qy qz Cos[phi] + (qx^2 + qy^2) Sin[phi]))/(
qx^2 Sin[phi] + qy^2 Sin[phi]), (
Cos[phi] ((-qx^2 + qy^2) qz + qy (qx^2 + qy^2) Tan[phi]))/(
qx^2 Sin[phi] + qy^2 Sin[phi])}]
cylindAnamorphic[{yi, zi}, phi] // Simplify
{yi (3 - 2 yi^2 + 2 Sqrt[1 - yi^2] zi Cot[phi]),
2 (1 - yi^2)^(3/2) + (zi - 2 yi^2 zi) Cot[phi], 0};
cylinderAmorphic[{yi_, zi_},
phi_] := {yi (3 - 2 yi^2 + 2 Sqrt[1 - yi^2] zi Cot[phi]),
2 (1 - yi^2)^(3/2) + (zi - 2 yi^2 zi) Cot[phi]}
The inverse function for the coordinates of the reflection P given those of the anamorphic map S and the view direction phi is derived below:
cylinderReflection[{xr_, yr_}, phi_] :=
Re /@ First[
Select[{yi, zi} /.
Solve[{xr,
yr} == {yi (3 - 2 yi^2 + 2 Sqrt[1 - yi^2] zi Cot[phi]),
2 (1 - yi^2)^(3/2) + (zi - 2 yi^2 zi) Cot[phi]}, {yi, zi}],
Last[#] > 0 &]]
Here we can test the effectiveness of the two inverse functions cylinderAmorphic and cylinderReflection. We apply to a random point S in the x-y plane:
phi = RandomReal[{5., 85.}]; Degree; pt =
RandomReal[{-10, 10}, {2}]; Rasterize@pt
cylinderAmorphic[cylinderReflection[pt, phi], phi] // Rasterize

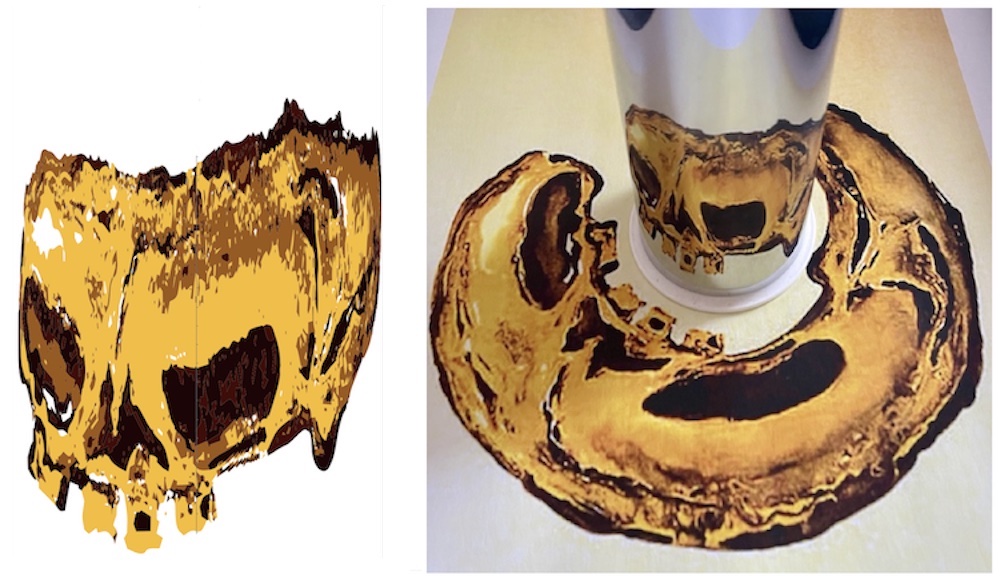
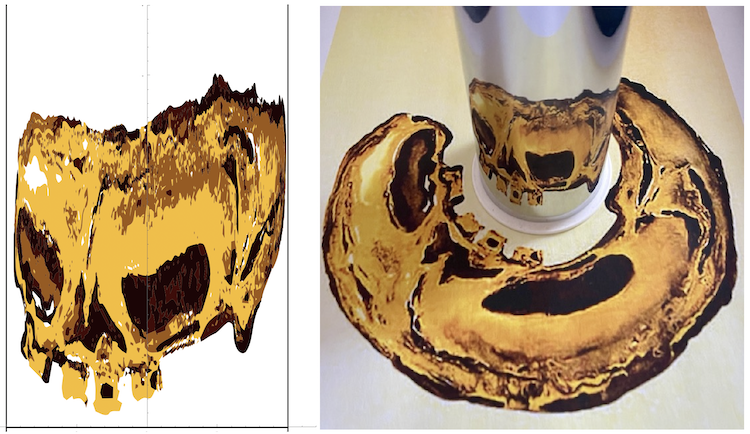
With the function cylinderReflection, we can now reconstruct the skull without the use of a mirror! We take the Dalí lithograph (Le Crâne or The Skull, attached at the end as: "le crane.jpg" ) as the anamorphic version and find the original "hidden" image.
anaCrane = Import[.../"le crane.jpg" ];
craneIG = ImageGraphics[ImageReflect[anaCrane, Left], 5]
The original instructions from archivist Albert Field were as follows: "putting a cylindrical mirror about 3 inches in diameter at a specific spot gives a new image". The lithograph is about 75cm x 56cm. The printout I will use is on an A4 sheet and, to be proportional, I used a cylinder of 7.5 X 25/56 or about 3.5 cm diameter.
craneComplex =
craneIG[[
1]] /. {x_?(And[NumericQ[#], Not[IntegerQ[#]]] &),
y_} :> {x - 175, y - 125}/25;
Graphics[{craneComplex, {Dashed, Circle[]}}, Axes -> True,
AxesOrigin -> {0, 0}];
reflectCrane =
Quiet@MapAt[cylinderReflection[#, 23.5 °] &, craneComplex, {1, All}];
Graphics[{{Line[{{-1, -1}, {-1, 4}}], Line[{{1, -1}, {1, 4}}],
Line[{{-1, 0}, {1, 0}}]}, reflectCrane}, Axes -> True,
TicksStyle -> 1, PlotRange -> {{-1.2, 1.2}, {0, 3}}]
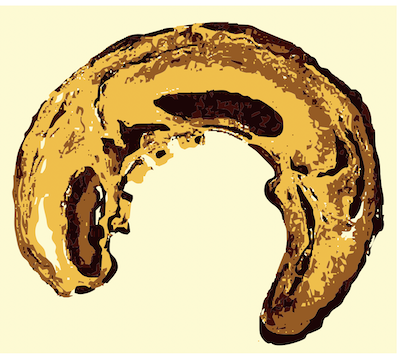
Using the inverse function cylinderAmorphic, we can make our own Dalí type "anamorphose". We use use the image of a human skull from e.g shutterstock.com. (attached as "skull.png")
skull = ImageResize[ImageAdjust@ Import[.../"skull.jpg" ], 500] ;
This converts the image to a GraphicsComplex:
skullIG = ImageGraphics[skull, 10]

Mapping cylinderAmorphic to the point coordinates in the GraphicsComplex gives an anamorphic map of the skull graphic:

As with the Dalí lithograph, putting a cylindrical mirror of the right diameter in the right spot, we see a reflection of the original skull image.

Anamorphism was one of the illusions frequently used by Dalí and similar works could be analysed the same way as above. However, the galleries, selling these lithographs for thousands of dollars, seem to have lost any notion of the original intent of the works. Some even recommend it using as a vertical wall decoration! The admirer would have to try putting a cylindrical mirror perpendicular to the wall and in the middle of the picture to observe the image originally intended by Dalí! Or use Mathematica!

MODERATOR NOTE: the following are original sources of the used images
Skull
Le Crane