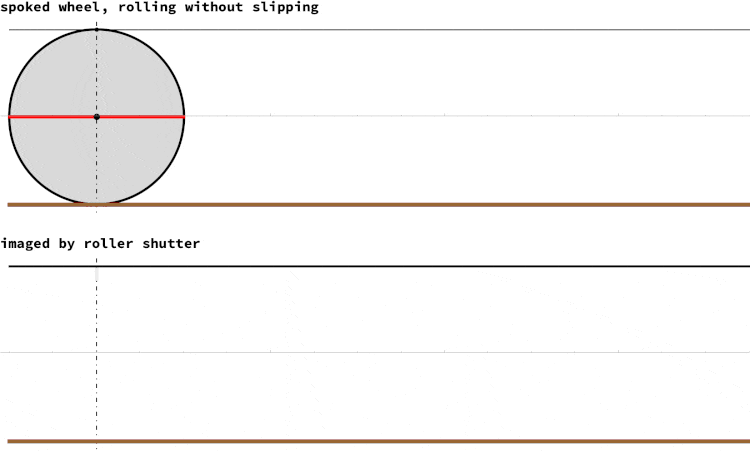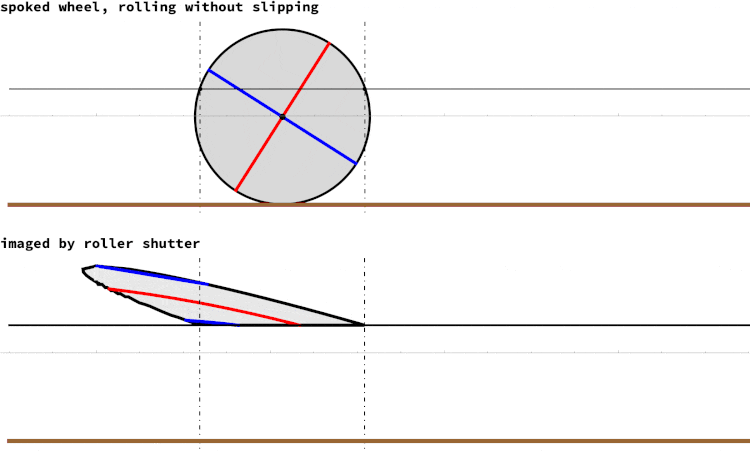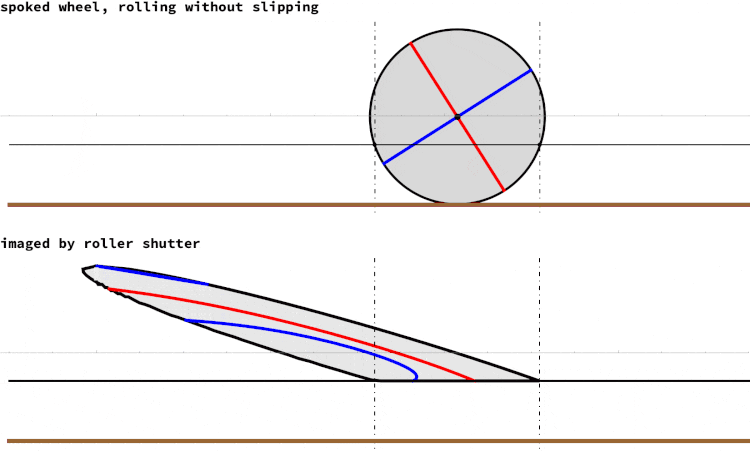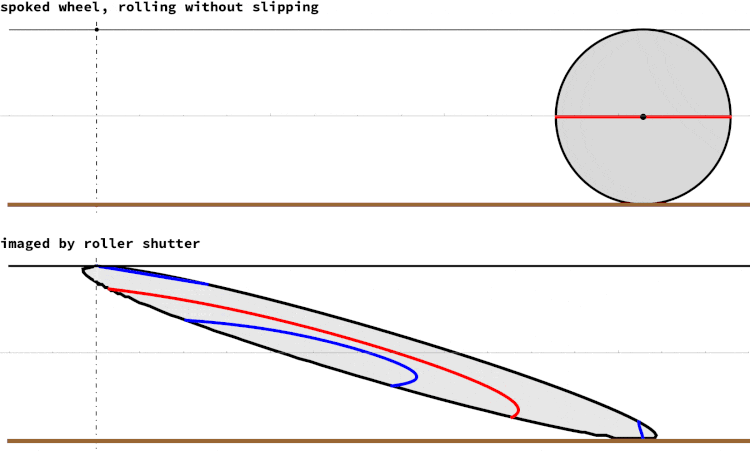
A rolling camera shutter operates by sequentially exposing the image sensor, capturing one line at a time starting from the top and moving downwards. In contrast, a global shutter exposes the entire sensor simultaneously. When photographing fast-moving objects, the rolling shutter can introduce a distinctive distortion known as the "rolling shutter effect." The accompanying image illustrates this phenomenon. The top portion depicts a spoked wheel rolling smoothly without slipping, while the bottom portion represents the corresponding image traced by a rolling shutter. The rotational speed of the wheel in revolutions per second is equal to the frame rate of the camera shutter. Previous contributions from the community regarding the rolling shutter effect mainly focused on capturing images of rotating objects with distinct lines, such as propellers.

Airplane propellers imaged with a rolling shutter by Greg Hurst

Modelling the Rolling Shutter Effect by Christopher Grattoni

Rolling Shutter III by Hendrik Schachner

... or a rotating disk:

Imaging a rotating disk with a rolling shutter by Erik Mahieu,

In this contribution, we explore the combination of rotating lines and a disk within a spoked wheel. Unlike previous examples, the wheel in question is not rotating around a fixed axis but rather rolling without slipping along a horizontal line.

This is the parametric expression of a rolling shutter: a horizontal line moving cyclically between y=+r and y=-r at a constant speed v:

{v*t + r Cos[p], 1 - 2 Mod[t, 1]}

This is the parametric equation of a circle of radius r rolling without slipping at a constant speed v over a horizontal line:

{t + r Cos[2 \[Pi] v t], r Sin[2 \[Pi] v t]}

These are the two intersection points:

{v*t + r Cos[p], r Sin[p]} /. 
    Solve[{v*t + r Cos[p], r Sin[p]} == {v*t + r Cos[p], 
       1 - 2 Mod[t, 1]}, p, Reals] // FullSimplify // 
  Normal // Rasterize

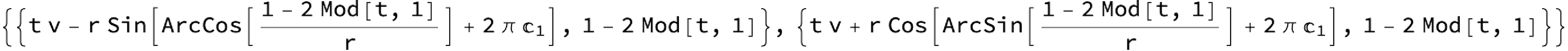
The function circle2ShutterIntersect computes these intersection point coordinates:

circle2ShutterIntersect[t_, v_, 
  r_] := {{v t - r Cos[ArcSin[(1 - 2 Mod[t, 1])/r]], 
   1 - 2 Mod[t, 1]}, {v t + r Cos[ArcSin[(-1 + 2 Mod[t, 1])/r]], 
   1 - 2 Mod[t, 1]}}

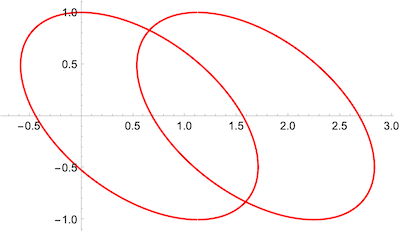
This shows the locus of Intersection points for a descending line from top to bottom for 2 passes of the shutter:

Module[{v = 1.123, r = 1}, 
 ParametricPlot[circle2ShutterIntersect[t, v, r], {t, 0, 2.00001}, 
  PlotPoints -> 1000, PlotStyle -> Red]]

This is an animation showing 3 passes of the rolling shutter intersecting the rolling circle:

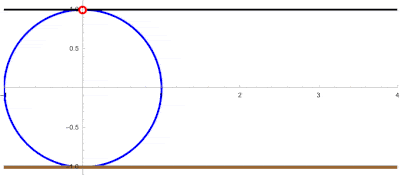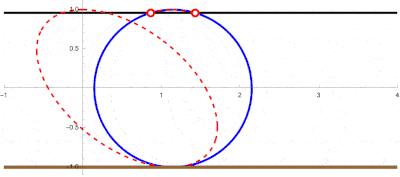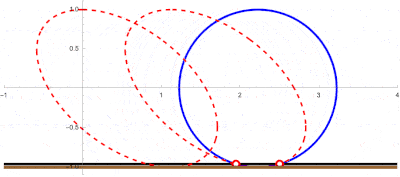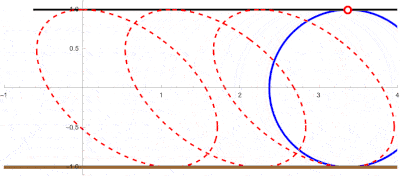
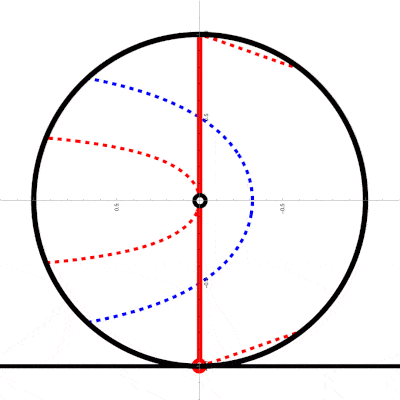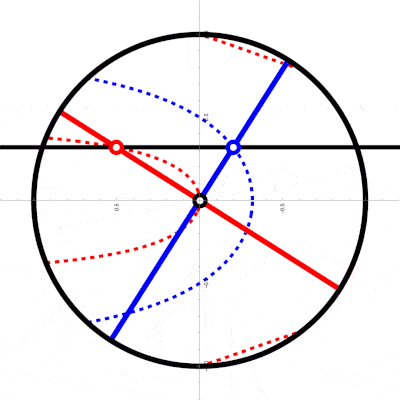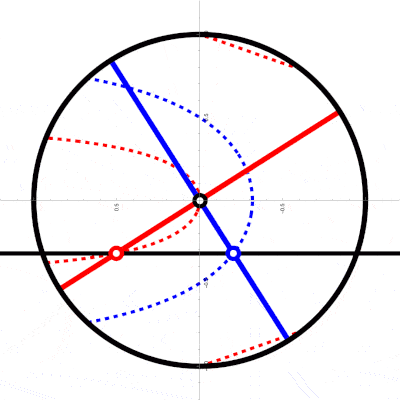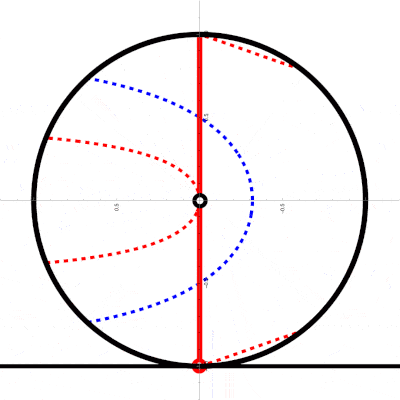
If the circle is only rotating around a fixed center, the spokes are in fact rotating lines forming a type of propeller and we can use some of the code of the notebook mentioned above:

spoke2ShutterIntersect[t_, 
  v_, \[Alpha]_ : 0] := {-1 + 
   2 Mod[t, 1], (-1 + 2 Mod[t, 1]) Tan[2 \[Pi] t v + \[Alpha]]}

With[{v = 1, r = 1}, 
 Animate[Graphics[{ParametricPlot[
      spoke2ShutterIntersect[t, v, 0], {t, 0, .999}, 
      PlotStyle -> Directive[Dashed, AbsoluteThickness[3], Red], 
      RegionFunction -> Function[{x, y, p}, 0 < Norm[{x, y}] <= 1]][[
     1]], ParametricPlot[
      spoke2ShutterIntersect[t, v, Pi/2], {t, 0, .999}, 
      PlotStyle -> Directive[Dashed, AbsoluteThickness[3], Blue], 
      RegionFunction -> Function[{x, y, p}, 0 < Norm[{x, y}] <= 1]][[
     1]], ParametricPlot[{p, p Tan[2 Pi v t]}, {p, -2, 2}, 
      PlotStyle -> Directive[AbsoluteThickness[5], Red], 
      RegionFunction -> Function[{x, y, p}, 0 < Norm[{x, y}] < 1]][[
     1]], ParametricPlot[{p, p Tan[2 Pi v t + Pi/2]}, {p, -2, 2}, 
      PlotStyle -> Directive[AbsoluteThickness[5], Blue], 
      RegionFunction -> Function[{x, y, p}, 0 < Norm[{x, y}] < 1]][[
     1]], {Directive[AbsoluteThickness[4], Black], 
     Line[{{-1 + 2 Mod[t, 1], -2}, {-1 + 2 Mod[t, 1], 
        2}}]}, {AbsolutePointSize[14], Black, Point[{0, 0}], 
     AbsolutePointSize[6], White, 
     Point[{0, 0}]}, {AbsolutePointSize[14], Red, 
     Point[spoke2ShutterIntersect[t, v, 0]], Blue, 
     Point[spoke2ShutterIntersect[t, v, Pi/2]], AbsolutePointSize[6], 
     White, Point[{spoke2ShutterIntersect[t, v, 0], 
       spoke2ShutterIntersect[t, v, Pi/2]}]}, {Directive[
      AbsoluteThickness[5], Black], Circle[]}}, PlotRange -> 1.2], {t,
    1., 0., -.02}]]

When the circle is rolling without slipping, we need a new function :

wheel2ShutterIntersect[t_, 
  v_, \[Alpha]_ : 
   0] := {2 Pi v t + (-1 + 2 Mod[t, 1]) Cot[
     2 Pi t v + \[Alpha]] , -(-1 + 2 Mod[t, 1])}

Now the animation looks like this:

With[{v = 1, r = 1}, 
 Animate[Graphics[{{AbsoluteThickness[5], Circle[{2 Pi v tt, 0}, 1], 
     LightGray, Disk[{2 Pi v tt, 0}, 1]}, 
    ParametricPlot[wheel2ShutterIntersect[t, v, 0], {t, .001, 0.999}, 
      RegionFunction -> 
       Function[{x, y, t}, 
        Norm[{x - 2 Pi v t, y}] <= 1 && y > 1 - 2 tt], 
      PlotStyle -> Directive[AbsoluteThickness[2], Red]][[1]], 
    ParametricPlot[
      wheel2ShutterIntersect[t, v, Pi/2], {t, .001, 0.999}, 
      RegionFunction -> 
       Function[{x, y, t}, 
        Norm[{x - 2 Pi v t, y}] <= 1 && y > 1 - 2 tt], 
      PlotStyle -> Directive[AbsoluteThickness[2], Blue]][[1]], 
    ParametricPlot[{{s (2 Pi p v - Sqrt[1 - (1 - 2 Mod[p, 1])^2]), 
        1 - 2 Mod[p, 1]}, {s (2 Pi p v + Sqrt[
           1 - (1 - 2 Mod[p, 1])^2]), 1 - 2 Mod[p, 1]}}, {p, 
       0, .99}, {s, 0, 1.}, PlotStyle -> Lighter[Gray, .35], 
      BoundaryStyle -> Directive[AbsoluteThickness[2.5], Black], 
      RegionFunction -> 
       Function[{x, y, t}, 
        Norm[{x - 2 Pi v t, y}] <= 1 && y > 1 - 2 tt]][[1]], 
    ParametricPlot[{2 Pi v tt + p, p Tan[-2 Pi v tt]}, {p, -1, 1}, 
      PlotStyle -> Directive[Red, AbsoluteThickness[2]], 
      RegionFunction -> 
       Function[{x, y, p}, Norm[{x - 2 Pi v tt, y}] <= 1]][[1]], 
    ParametricPlot[{2 Pi v tt + p, p Tan[-2 Pi v tt + Pi/2]}, {p, -1, 
       1}, PlotStyle -> Directive[Blue, AbsoluteThickness[2]], 
      RegionFunction -> 
       Function[{x, y, p}, Norm[{x - 2 Pi v tt, y}] <= 1]][[
     1]], {AbsolutePointSize[6], 
     Point[{2 Pi v tt, 0}]}, {Directive[AbsoluteThickness[2], Black], 
     Line[{{-1, 1 - 2 Mod[tt, 1]}, {10, 1 - 2 Mod[tt, 1]}}]}, 
    If[Norm[{wheel2ShutterIntersect[tt, v, 0][[1]] - 2 Pi v tt, 
        wheel2ShutterIntersect[tt, v, 0][[2]]}] <= 
      1, {AbsolutePointSize[9], Red, 
      Point[wheel2ShutterIntersect[tt, v, 0]], AbsolutePointSize[4], 
      White, Point[{wheel2ShutterIntersect[tt, v, 0]}]}, {}], 
    If[Norm[{wheel2ShutterIntersect[tt, v, Pi/2][[1]] - 2 Pi v tt, 
        wheel2ShutterIntersect[tt, v, Pi/2][[2]]}] <= 
      1, {AbsolutePointSize[9], Blue, 
      Point[wheel2ShutterIntersect[tt, v, Pi/2]], 
      AbsolutePointSize[4], White, 
      Point[{wheel2ShutterIntersect[tt, v, Pi/
         2]}]}, {}], {AbsolutePointSize[10], Black, 
     Point[Re[circle2ShutterIntersect[tt, 2 Pi v, 1]]], 
     AbsolutePointSize[4], White, 
     Point[Re[
       circle2ShutterIntersect[tt, 2 Pi v, 1]]]}, {AbsoluteThickness[
      4], Brown, 
     Line[{{-1, -1 - .01}, {10, -1 - .01}}]}, {AbsoluteThickness[4], 
     White, Line[{{0, .86}, {0, .96}}], Lighter[Gray, .85], 
     Line[{{0, .86}, {0, .96}}]}}], {tt, 0., 1, .02}]]