RectanglePacking - A Wolfram Language package for 2D bin packing

A few years ago I found myself needing to take a bunch of 2D objects and arrange them together in a compact space so that they don't overlap. Searching on the web I found out I was facing a packing problem, specifically rectangle packing.
I found the paper "A Thousand Ways to Pack the Bin - A Practical Approach to Two-Dimensional Rectangle Bin Packing." by Jukka Jylänki, along with a C++ library implementing the algorithms described in the paper.
I was able to use that library to solve my problem, at the time thinking "This would be a useful tool to make available to Wolfram Language users." But I didn't know an easy way to package up my code, which uses LibraryLink to call the C++ functions, in a way that could be used by the Wolfram Function Repository. So it sat in my unfinished projects folder and I moved on.
I recently looked back at this project and decided to share it via the Wolfram Paclet Repository, since it can easily work with LibraryLink. The package is called RectanglePacking and can be installed in any Mathematica version 13 or higher with the commands
(* install the paclet *)
PacletInstall["JasonB/RectanglePacking"]
(* load the package *)
Needs["JasonB`RectanglePacking`"]
There are two functions in this package, PackRectangles and RectanglePacker. The first function is quite simple
In[6]:= ?PackRectangles
Out[6]= "PackRectangles[boundingbox,{rect1,rect2,..}] packs the given rectangles in the given bounding box.
PackRectangles[boundingbox,rectangles,method] uses the given method to pack rectangles."
Here boundingbox is a pair of integers representing the width and height of the bounding rectangle, and rectangles is a list of (a) width-height pairs or (b) explicit Rectangle objects. Note all coordinates need to be integers. The full list of methods can be obtained from the symbol $RectanglePackingMethods.
Let's start by generating some rectangles and packing them in a 100 by 100 area:
In[71]:= toPack = Table[{n, Floor[5 n/4]}, {n, 28}];
packed = PackRectangles[{100, 100}, toPack];
Short[packed]
Out[73]//Short= {{{26,99},{27,100}},{{30,65},{32,67}},<<24>>,{{0,35},{27,68}},{{0,0},{28,35}}}
The output is a list of {{xmin, ymin},{xmax,ymax}} representing the packed rectangles. Here is a graphical representation:
Graphics[{FaceForm[LightYellow], EdgeForm[Black], Rectangle @@@ packed}, Frame -> True]
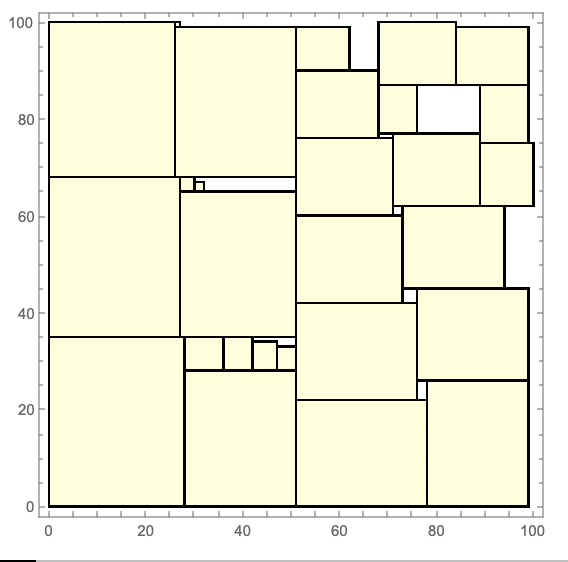
The above function is perfect when you have a set list of rectangles and want to pack them in any order. You can also create a mutable data structure for sequential rectangle packing:
packer = RectanglePacker[{300, 150}]
The RectanglePacker object has methods for inserting rectangles and visualization:
SeedRandom[1978];
packer["Insert", RandomInteger[{2, 42}, {30, 2}]];
packer["Graphics"]
packer["Insert", RandomInteger[{2, 42}, {30, 2}]];
packer["Graphics"]

You can visualize the different packing methods described in the paper linked above:
SeedRandom @ 1978;
rects = RandomInteger[{6, 24}, {200, 2}];
plots = Map[
Function[
With[{packer = JasonB`RectanglePacking`RectanglePacker[{300, 150}, #]},
packer["Insert", rects];
packer["Graphics", PlotLabel -> #, ImageSize -> 200]
]
],
{"MaxRects", "Guillotine", "Shelf", "Skyline"}
];
Grid @ Partition[plots, 2]

I hope people find these functions useful. If you have any suggestions or bugs please create an issue on the github page.