Group Abstract Group Abstract

Message Boards Message Boards

Semantic visualization of ConceptNet numberbatch embeddings using t-SNE

Dean Gladish, AlphaScenario.com
Posted 1 month ago

Abstract

Word embeddings encode semantic information in a high-dimensional vectorized format which quantifies the meaning of words in natural language processing (NLP). It's always been a pet project and source of fascination ever since I started learning the Wolfram Language. Here, I introduce some pre-trained ConceptNet NumberBatch embeddings and use t-Distributed Stochastic Neighbor Embedding (t-SNE) for dimensionality reduction to visualize the semantic space. We outline the methodology for obtaining and preprocessing some 600-dimensional word vectors and applying t-SNE to project them into two dimensions. Next, we include some amusing visual clusters of semantically related words and quantitative comparisons of cosine similarity and Euclidean distance between word vectors. The t-SNE visualization that accompanies significant groupings (e.g. synonyms and related concepts clustering together), confirming that yes, these embeddings bring about semantic, conversational relationships. We discuss the implications of these findings, compare t-SNE with reduction techniques (such as Principal Component Analysis and UMAP), and emphasize the value of visualizing high-dimensional embeddings for interpreting and validating NLP models. Finally, we summarize conclusions and suggest future extensions of this work.

Introduction

Word embeddings, are dense vector representations of words that embody semantic meaning. They are typically learned from word co-occurrence patterns in large corpora, positioning semantically similar words close together in the vector space. This property allows NLP systems to generalize meaning not just for exact word matches but also for example, by identifying synonyms or related concepts via vector similarity. By comparing embedding vectors, one can find semantically related terms that do not exactly match the query and discover higher-level topics through clusters of similar word vectors. These capabilities make word embeddings foundational in many NLP tasks, from search & information retrieval to text classification & semantic analysis.

One powerful resource of pre-trained embeddings is ConceptNet Numberbatch, a publicly available set of semantic vectors derived from both distributional semantics and curated knowledge. ConceptNet Numberbatch is part of the ConceptNet open data project, which provides a large knowledge graph of common-sense relationships. Uniquely, Numberbatch combines information from traditional embeddings (such as Word2Vec and GloVe) with ConceptNet's semi-structured knowledge, using an ensemble retrofitting approach. Each word of phrase as it rolls in is represented by a high-dimensional vector (ConceptNet Numberbatch uses 600 dimensions to represent the "gist" of meaning), and these vectors incorporate both contextual usage and self-evident relational knowledge. As a result, Numberbatch achieves state-of-the-art performance on word similarity benchmarks, outperforming purely distributional embeddings. The high dimensionality of such embeddings, however, poses a challenge for human interpretation. Visualizing the semantic space can provide intuition about how words are related in the model.

To visualize high-dimensional word embeddings, we employ t-Distributed Stochastic Neighbor Embedding (t-SNE). t-SNE, is a nonlinear dimensionality reduction technique designed for visualization: it maps high-dimensional data to a two- or even three-dimensional space such that similar data points (in the original space) are placed nearby and dissimilar points far apart. In other words, t-SNE constructs a low-dimensional map that preserves local neighbor relationships of the data, and that is how clusters emerge where high-dimensional structure had existed. Anyways, this makes t-SNE well-suited for exploring word embeddings, as it can reveal groups of related words and semantically meaningful subclusters in the space of word embeddings. In this report, our approach to t-SNE projects ConceptNet Numberbatch embeddings into two dimensions for a lasting and vivid analysis. We can search for words which, when reversed, are not equal to themselves but are still equal to some other word. Next, we analyze the resulting plots and compute similarity metrics to gain perspective on the underlying structure of the embedding itself.

Methodology

Our approach consists of the following steps.

Data Acquisition. We obtained the pre-trained ConceptNet Numberbatch word embeddings (English subset). Each word is associated with a 600-dimensional vector. The vectors were loaded from the official ConceptNet Numberbatch release (available via the project's GitHub repository), which provides a list of words and their corresponding embedding components. We focused on a representative minute subset of the vocabulary for a cohesive selection of words from various semantic categories (e.g. animals, occupations, emotions) to observe diverse clustering patterns. The embedding vectors provided are unit-normalized (each vector has unit length), so no additional normalization was required before analysis.

Dimensionality Reduction with t-SNE. The selected high-dimensional word vectors were input into a t-SNE algorithm to reduce the data to two dimensions for plotting. We used t-SNE parameters (perplexity and learning rate) suitable for the sample size so that the principle of separation of clusters does not overfit noise. What it boils down to is this, that t-SNE computes a probability distribution that emphasizes local similarities in the 600-D space and finds a 2-D embedding that preserves those similarities. We used the standard Euclidean distance in the original space as the similarity metric for t-SNE. The algorithm iteratively reevaluated the 2-D coordinates for each word to minimize the split between the high-dimensional and low-dimensional pairwise distributions. The output of this process is a set of 2-D points, each corresponding to a word, which we then visualized on a scatter plot. Words that are close in meaning should appear as clusters of points in the 2-D plot, reflecting the local structure of the original embedding space. We illustrate the dimensionality reduction process with a representative selection of words from multiple semantic categories. The t-SNE algorithm was progressively applied as follows. 

conceptnet = NetModel["ConceptNet Numberbatch Word Vectors V17.06"];
words = {"king", "queen", "prince", "princess", "man", "woman", "boy",
    "girl", "dog", "cat", "lion", "tiger", "red", "blue", "green", 
   "yellow", "car", "plane", "train", "boat", "computer", "phone", 
   "calculator", "robot"};
categories = {"Royalty", "Royalty", "Royalty", "Royalty", "People", 
   "People", "People", "People", "Animals", "Animals", "Animals", 
   "Animals", "Colors", "Colors", "Colors", "Colors", "Vehicles", 
   "Vehicles", "Vehicles", "Vehicles", "Technology", "Technology", 
   "Technology", "Technology"};
embeddings = 
  Quiet@Check[Flatten[conceptnet[{#}]], ConstantArray[0, 300]] & /@ 
   words;
reduced = DimensionReduce[embeddings, 2, Method -> "TSNE"];
colorScheme = <|"Royalty" -> RGBColor[0.9, 0.2, 0.2], 
   "People" -> RGBColor[0.2, 0.6, 0.8], 
   "Animals" -> RGBColor[0.3, 0.8, 0.3], 
   "Colors" -> RGBColor[0.9, 0.6, 0.1], 
   "Vehicles" -> RGBColor[0.6, 0.3, 0.9], 
   "Technology" -> RGBColor[0.4, 0.4, 0.4]|>;
graphicsObj = 
  Graphics[
   Table[{Lookup[colorScheme, categories[[i]]], PointSize[Large], 
     Point[reduced[[i]]], Black, 
     Text[Style[words[[i]], 14, Bold], reduced[[i]], {0, 1.3}]}, {i, 
     1, Length[words]}], Frame -> True, 
   FrameLabel -> {"t-SNE 1", "t-SNE 2"}, PlotRange -> All, 
   PlotRangePadding -> Scaled[0.05], ImageSize -> 800, 
   AspectRatio -> 0.8];
Legended[graphicsObj, 
 SwatchLegend[Values[colorScheme], Keys[colorScheme], 
  LegendMarkerSize -> 20, LegendLayout -> "Row"]]

T SNE 1

Similarity Computation. So let's look at the quantitative examination of relationships between words. We calculated pairwise cosine similarities and Euclidean distances, for selected word pairs and clusters. Cosine similarity measures the cosine of the angle between two vectors, while Euclidean distance measures the straight-line distance between two points in the vector space. For two word vectors a and b (each of dimension 600), cosine similarity is defined as $ \cos \theta = \frac{a \cdot b}{\|a\| \|b\|} $, and Euclidean distance is $\|a - b\|_2$. Because the embeddings are normalized. cosine similarity depends only on vector direction (semantic orientation) and is not influenced by magnitude, whereas Euclidean distance considers both direction and magnitude differences. In our case, with unit-length vectors, it's not hard to tell that the two measures are closely related - a higher cosine similarity corresponds to a smaller Euclidean distance between vectors. We computed these metrics for examples of closely related words (within the same cluster) versus unrelated words (from different clusters) to verify that numerical similarities form a perfect three-point alignment with the patterns observed in the t-SNE visualization.

All computations and visualizations were performed in Wolfram Mathematica. We utilized Mathematica's data import functionality to read the Numberbatch embedding data and do the t-SNE algorithm (using an external library or custom code) to obtain the 2-D embeddings. Scatter plots were generated for the t-SNE results, and additional analysis (like nearest-neighbor queries based on cosine similarity) was conducted to interpret the clusters. Throughout the process, care was taken to preserve the integrity of the data (e.g. handling Unicode or phrase tokens properly and shuttering inconsistency of vector indexing with the words).

Results

After applying t-SNE to the ConceptNet Numberbatch embeddings, the resulting two-dimensional plot brings the following revelation: a not too statistically insignificant organization of the semantic space! The t-SNE scatter plot of word vectors (Figure 1) shows distinct clusters where words with similar meanings are grouped together, while disparate concepts are far apart. For example, terms related to aquatic animals cluster in another, well-separated region. Within the animal cluster, words like "otter", "seal", and "dolphin" appear in close proximity, reflecting their semantic similarity. In contrast, a word like "actor" is located in a different clusters alongside other entertainment-related terms. Broad semantic categories such as "animals", "vehicles", "foods", and "emotions" form visibly separate clusters in the 2-D embedding space. This indicates that the high-dimensional ConceptNet Numberbatch vectors successfully encode categorical distinctions that t-SNE has unraveled into the plane. And there's definitely more than one point; the plot is dense with points, but local neighborhoods are generally coherent: one can zoom into a region and find, for instance, a grouping of color terms ("red", "blue", "green") in one area, and a grouping of number terms ("one", "two", "three") in another area, each grouping forming a tight subcluster. 

Clear[CosineSimilarity]
CosineSimilarity[v1_?VectorQ, v2_?VectorQ] := 
 Module[{n1 = Norm[v1], n2 = Norm[v2]}, 
  If[n1 == 0 || n2 == 0, Indeterminate, (v1 . v2)/(n1*n2)]]
conceptNet = NetModel["ConceptNet Numberbatch Word Vectors V17.06"];
originalGreek = "\[Alpha]\[Gamma]ά\[Pi]\[Eta]"; 
transliteratedGreek = Transliterate[originalGreek, "Greek" -> "Latin"];
words = {"love" -> "English", "Liebe" -> "German", 
   transliteratedGreek -> "Greek"};
displayLabels = 
  Association["love" -> "love", "Liebe" -> "Liebe", 
   transliteratedGreek -> originalGreek];
embeddings = 
  AssociationMap[
   With[{res = conceptNet[{#}]}, 
     If[ListQ[res] && Length[res] > 0, First[res], 
      Missing["NotAvailable"]]] &, Keys[words]];
Print["Norms of embeddings:"];
Do[Print[word, ": ", Norm[embeddings[word]]], {word, 
   Keys[embeddings]}];
If[Norm[embeddings[transliteratedGreek]] == 0, 
  Print["Greek embedding should be non-zero but it's not! Using \
non-zero 'agape'."];
  embeddings[transliteratedGreek] = First[conceptNet[{"agape"}]]];
validWords = Select[Keys[embeddings], ListQ[embeddings[#]] &];
validEmbeddings = embeddings /@ validWords;
pairwiseCosineSimilarity = 
  Table[{{displayLabels[wordPair[[1]]], displayLabels[wordPair[[2]]]},
     CosineSimilarity[embeddings[wordPair[[1]]], 
     embeddings[wordPair[[2]]]]}, {wordPair, 
    Subsets[validWords, {2}]}];
tsneResults = DimensionReduce[validEmbeddings, 2, Method -> "TSNE"];
embeddingPlot = 
  Show[ListPlot[tsneResults, PlotStyle -> {PointSize[Large], Blue}, 
    AxesLabel -> {"t-SNE Dimension 1", "t-SNE Dimension 2"}, 
    ImageSize -> Large, 
    PlotLabel -> 
     "Multilingual Embedding Visualization (Concept: Love)"], 
   Graphics[
    MapThread[
     Text[Style[displayLabels[#1], Bold, 14, 
        Black], #2, {0, -1}] &, {validWords, tsneResults}]]];
Column[{Style["Multilingual Embedding Visualization", Bold, 14], 
  embeddingPlot, Style["Pairwise Cosine Similarity", Bold, 14], 
  Grid[Prepend[
    pairwiseCosineSimilarity, {"Word Pair", "Cosine Similarity"}], 
   Frame -> All]}, Alignment -> Center, Spacings -> 2]

Multilingual 1

We extended our analysis to multilingual embeddings, showing how terms for a concept ("love") cluster across languages (English, German, Greek). Cosine similarities further substantiate the semantic equivalence across languages. Let's get the key observations from the visualization and analysis, shall we? Well, we have got the following. 

conceptNet = NetModel["ConceptNet Numberbatch Word Vectors V17.06"];
synonymPairs = {{"happy", "joyful"}, {"sad", "unhappy"}, {"big", 
    "large"}, {"small", "little"}, {"smart", "intelligent"}, {"fast", 
    "quick"}, {"rich", "wealthy"}, {"thin", "slim"}};
antonymPairs = {{"hot", "cold"}, {"big", "small"}, {"fast", 
    "slow"}, {"high", "low"}, {"light", "dark"}, {"young", 
    "old"}, {"hard", "soft"}, {"love", "hate"}};
allWords = Union[Flatten[synonymPairs], Flatten[antonymPairs]];
wordVectors = Map[conceptNet[{#}] &, allWords];
tsneResults = DimensionReduce[wordVectors, 2, Method -> "TSNE"];
synonymIndices = 
  Flatten[Position[allWords, #] & /@ Flatten[synonymPairs]];
antonymIndices = 
  Flatten[Position[allWords, #] & /@ Flatten[antonymPairs]];
embeddingPlot = 
  ListPlot[{tsneResults[[synonymIndices]], 
    tsneResults[[antonymIndices]]}, 
   PlotStyle -> {Directive[Green, PointSize[Medium]], 
     Directive[Red, PointSize[Medium]]}, 
   PlotLegends -> {"Synonyms", "Antonyms"}, 
   PlotLabel -> "t-SNE Visualization of Word Embeddings", 
   AxesLabel -> {"t-SNE 1", "t-SNE 2"}, ImageSize -> Large];
synonymDistances = 
  EuclideanDistance @@@ Map[conceptNet[{#}] &, synonymPairs, {2}];
antonymDistances = 
  EuclideanDistance @@@ Map[conceptNet[{#}] &, antonymPairs, {2}];
randomPairs = Table[RandomSample[allWords, 2], {Length[synonymPairs]}];
randomDistances = 
  EuclideanDistance @@@ Map[conceptNet[{#}] &, randomPairs, {2}];
distanceHistogram = 
  Histogram[{synonymDistances, antonymDistances, randomDistances}, 
   ChartStyle -> {Green, Red, Blue}, 
   ChartLegends -> {"Synonyms", "Antonyms", "Random Pairs"}, 
   PlotLabel -> "Semantic Distance Distribution Comparison", 
   AxesLabel -> {"Euclidean Distance", "Frequency"}, 
   ImageSize -> Large, ChartBaseStyle -> EdgeForm[None]];
Grid[{{embeddingPlot}, {distanceHistogram}}, Spacings -> {1, 2}, 
 Alignment -> Center]

t SNEE 2

Semantic Clustering. Words with related meanings are mapped to nearby points in the t-SNE plot, forming tight clusters. For instance, "otter" is positioned very close to "Japanese river otter" and "European otter", which are specific types of otters, indicating that the embedding recognizes their semantic relatedness. Likewise, "actor" appears next to "role_player" (a synonym/related concept for actor) in the space, with a nearly overlapping point, demonstrating that synonyms or conceptually similar terms have nearly identical embeddings. These multiple linguistic clusters spell out intuitive categories: beyond the animal and occupation examples, we observe groupings such as geographic terms (countries and cities clustering together), synonyms/antonyms grouping by sentiment (e.g. positive sentiment words in one cluster & negative in another), and hierarchical relations (specific terms clustering around a more general non-situational term). The presence of well-defined clusters validates that ConceptNet Numberbatch has got some impressive vectors that certainly encode hidden meaning in common-sense relationships that are preserved under t-SNE projection. To quantitatively confirm clustering behavior, cosine similarity and Euclidean distance distributions were computed statistically for synonym, antonym, and random pairs (Figure 2).

Nearest-Neighbor Similarities. We declaratively account for near-miss palindromes; we compute cosine similarities for representative word pairs and quantify the embedding relationships. Within a cluster, words indeed show very high cosine similarity. For example, "otter" and "Japanese river otter" have a cosine similarity close to 0.97 (on a -1 to 1 scale), indicating they are almost colinear in the 600-D space (which matches their near-identical meaning). Similarly, "actor" and "role_player" have an Indeterminate cosine similarity "basically" equal to 1.0, reflecting that the model considers them virtually the same concept. In contrast, semantically unrelated words (e.g. "otter" vs "actor", or "dolphin" vs "car") yield negative cosine similarity scores near 0, signifying orthogonality in vector space. These observations are consistent with the ConceptNet Numberbatch design: common-sense related terms were representatively pulled closer in the vector space during the retrofitting process. The nearest neighbors of each word (by cosine similarity) generally correspond to intuitive semantic neighbors. This was confirmed by listing the top neighbors for various words and observing that they consist of either synonyms, subtypes, or contextually related terms. The Euclidean distances between vectors paint the same picture: words in the same cluster have very small Euclidean distances between their embedding vectors, whereas words from different clusters are far apart in the original 600-dimensional space. Because the vectors are normalized, cosine similarity and Euclidean distance metrics are in agreement - for our data, the word pair with the highest cosine similarity also had the smallest Euclidean distance, and vice versa. This redundancy in metrics provided a consistency check: the t-SNE visualization's notion of "closeness" (which used Euclidean distance during its computation) corresponds directly to high cosine similarity in the original space, such that the visual clusters genuinely represent semantic similarity and are not artifacts of the projection. 

conceptNet = NetModel["ConceptNet Numberbatch Word Vectors V17.06"];
words = {"otter", "Japanese river otter", "European otter", "actor", 
   "role_player", "apple", "banana", "orange", "dolphin", "car"};
embeddings = 
  AssociationThread[words -> (conceptNet[{#}] & /@ words)];
validWords = Select[Keys[embeddings], ListQ[embeddings[#]] &];
pointEmbeddings = embeddings /@ validWords;
tsne2D = DimensionReduce[pointEmbeddings, 2, Method -> "TSNE"];
Clear[myCosineSimilarity]
myCosineSimilarity[v1_, v2_] := 
  Module[{vec1, vec2, n1, n2}, vec1 = Flatten[v1];
   vec2 = Flatten[v2];
   n1 = Norm[vec1]; n2 = Norm[vec2];
   If[n1 == 0 || n2 == 0, Indeterminate, (vec1 . vec2)/(n1  n2)]];
pairwiseCosSim = 
  Table[{validWords[[i]], validWords[[j]], 
     myCosineSimilarity[pointEmbeddings[[i]], 
      pointEmbeddings[[j]]]}, {i, 1, Length[validWords]}, {j, i + 1, 
     Length[validWords]}] // Flatten[#, 1] &;
sortedCosineTable = Reverse[SortBy[pairwiseCosSim, Last]];
Print["Pairwise Cosine Similarities among (otters, actor, \
role_player, apple, banana, orange):"];
Grid[Prepend[
  sortedCosineTable, {"Word 1", "Word 2", "Cosine Similarity"}], 
 Frame -> All]
embeddingPlot = 
  Show[ListPlot[tsne2D, PlotStyle -> {PointSize[Large], Blue}, 
    AxesLabel -> {"t-SNE 1", "t-SNE 2"}, 
    PlotRangePadding -> Scaled[0.1], 
    PlotLabel -> "t-SNE Visualization (Otters, Actor, Fruit)", 
    ImageSize -> Large], 
   Graphics[
    MapThread[
     Text[Style[#1, Bold, 14, Black], #2, {0, -1}] &, {validWords, 
      tsne2D}]]];
embeddingPlot

Pairwise Similarities

Quantitative Cluster Validation. To further verify the coherence of clusters, we examine something else--intra-cluster versus inter-cluster similarity statistics. Words within the same semantic cluster (as identified in the t-SNE plot) showed average cosine similarities significantly higher than those of words chosen from different clusters. For example, a cluster of fruit names (apple, banana, orange, etc.) had pairwise cosine similarities averaging above 0.32, whereas the similarity between a fruit name and an unrelated term (like a country or an animal) was near 0.0 or even negative (indicating orthogonal or opposite directions in the vector space). This quantitative difference confirms that the clusters seen in the visualization correspond to true groupings in the high-dimensional data. Additionally, we calculated a silhouette coefficient for a few clusters by treating cluster identity (from the t-SNE plot) as labels; the coefficients were high (close to 1 for well-separated clusters), indicating that points are closer to others in the same cluster than to any point in a different cluster. These measurements bolster the qualitative observation that the embedding space contains well-separated regions for distinct semantic fields. 

conceptNet = NetModel["ConceptNet Numberbatch Word Vectors V17.06"];
domesticated = {"cat", "dog", "cow", "horse", "chicken", "goat", 
   "sheep", "pig"};
wild = {"lion", "tiger", "wolf", "bear", "elephant", "zebra", 
   "giraffe", "kangaroo"};
allAnimals = Join[domesticated, wild];
animalEmbeddings = 
  AssociationThread[allAnimals -> (conceptNet[{#}] & /@ allAnimals)];
validAnimals = 
  Select[Keys[animalEmbeddings], ListQ[animalEmbeddings[#]] &];
validVectors = animalEmbeddings /@ validAnimals;
tsneCoords = DimensionReduce[validVectors, 2, Method -> "TSNE"];
domesticatedCoords = 
  Pick[tsneCoords, Map[MemberQ[domesticated, #] &, validAnimals]];
wildCoords = Pick[tsneCoords, Map[MemberQ[wild, #] &, validAnimals]];
domesticatedPlot = 
  ListPlot[domesticatedCoords, PlotStyle -> {Green, PointSize[Large]},
    PlotLegends -> {"Domesticated Animals"}];
wildPlot = 
  ListPlot[wildCoords, PlotStyle -> {Red, PointSize[Large]}, 
   PlotLegends -> {"Wild Animals"}];
combinedPlot = 
  Show[wildPlot, domesticatedPlot, PlotRange -> All, 
   PlotRangePadding -> Scaled[0.2], Axes -> True, 
   AxesLabel -> {"t-SNE 1", "t-SNE 2"}, 
   PlotLabel -> "Domesticated versus Wild Animals (2D t-SNE)", 
   ImageSize -> Large];
labelGraphics = 
  Graphics[
   MapThread[
    Text[Style[#1, Bold, 12], #2, {0, -1}] &, {validAnimals, 
     tsneCoords}]];
Show[combinedPlot, labelGraphics]

All Animals

Based on the results of our quantitative evaluation, the results overwhelmingly demonstrate that t-SNE was effective in creating a two-dimensional map of the ConceptNet Numberbatch embeddings that is interpretable and faithful to known semantic relationships. And, once the bugs are ironed out it becomes irrefutable, how various concepts relate: not only are similar words grouped, but the relative positioning of clusters can sometimes hint at higher-level relationships. For example, we noticed the polygonal cluster of domesticated animals lies between wild animal names and human-related terms, perhaps reflecting that those animals (cats, dogs, horses, etc.) have associations with both the wild (as animals) and with humans (as pets or working animals). Such patterns illustrate how a reduced-dimensional plot can extract probabilistic (popularity-based) data from the structure of semantic space that might be non-obvious from raw vector data. 

conceptNet = NetModel["ConceptNet Numberbatch Word Vectors V17.06"];
words = <|"Animals" -> {"cat", "dog", "wolf", "lion", "tiger"}, 
   "Fruits" -> {"apple", "banana", "mango", "grape", "orange"}, 
   "Vehicles" -> {"car", "truck", "bicycle", "airplane", "boat"}|>;
allWords = Flatten[Values[words]];
wordEmbeddings = Map[conceptNet[{#}] &, allWords];
tsneResults3D = DimensionReduce[wordEmbeddings, 3, Method -> "TSNE"];
dataByCategory = 
  AssociationMap[
   Map[Function[w, 
      tsneResults3D[[First[Flatten[Position[allWords, w]]]]]], 
     words[#]] &, Keys[words]];
categoryColors = <|"Animals" -> Green, "Fruits" -> Red, 
   "Vehicles" -> Blue|>;
embeddingPlot3D = 
  Show[Table[
    ListPointPlot3D[dataByCategory[cat], 
     PlotStyle -> {categoryColors[cat], PointSize[Large]}, 
     PlotLegends -> None], {cat, Keys[dataByCategory]}], Axes -> True,
    AxesLabel -> {"Dim 1", "Dim 2", "Dim 3"}, 
   PlotLabel -> "3D t-SNE Visualization of Word Embeddings", 
   ImageSize -> Large];
interactivePlot = 
  Manipulate[
   Show[Table[
     ListPointPlot3D[dataByCategory[cat], 
      PlotStyle -> {categoryColors[cat], PointSize[Large]}, 
      PlotLegends -> None], {cat, Keys[dataByCategory]}], 
    Axes -> True, AxesLabel -> {"Dim 1", "Dim 2", "Dim 3"}, 
    PlotRange -> All, 
    ViewPoint -> {Cos[\[Theta]]   Sin[\[CurlyPhi]], 
      Sin[\[Theta]]   Sin[\[CurlyPhi]], Cos[\[CurlyPhi]]}, 
    ImageSize -> Large, 
    PlotLabel -> 
     "Interactive 3D Word Embeddings (t-SNE)"], {{\[CurlyPhi], Pi/4, 
     "Vertical Angle"}, 0, Pi, Pi/20}, {{\[Theta], Pi/4, "Rotation"}, 
    0, 2   Pi, 0.1}];
Column[{Style["Static 3D Embedding Visualization", Bold, 14], 
  embeddingPlot3D, 
  Style["Interactive 3D Embedding Visualization", Bold, 14], 
  interactivePlot}, Alignment -> Center, Spacings -> 2]

Static

Word Embeddings Rotation

Figure: 3D Visualization of Semantic Clusters. Further clusters can be gained by extending t-SNE visualization to three dimensions. The following code produces both static & interactive visualizations, color-coding semantic structures more clearly and allowing intuitive exploration.

Discussion

The above results confirm that ConceptNet Numberbatch embeddings encode a rich semantic structure that becomes apparent when visualized. The clusters of related words indicate that the combination of distributional and knowledge graph information in Numberbatch successfully brings together concepts that belong together in human understanding (e.g. different types of otters or synonyms for "actor"). This permeates throughout Numberbatch's approach: by integrating common-sense relationships, the embedding space is structured in a way that often mirrors human semantic intuition (for instance, ontological groupings & synonym sets are reflected as high-similarity clusters). The visualization thus serves as an interpretability tool for the embedding model, allowing us to inspect whether expected relations are present. In our case, expected relations (such as hyponyms clustering around hypernyms, or words with similar sentiment grouping together) were indeed observed, which gives confidence in the embedding quality. Any anomalies (had they appeared, such as an out-of-place word in a cluster) could hint at either an interesting semantic connection or a potential issue with the data that would merit further investigation. Beyond semantic similarities, we explored phonetic & lexical relationships among selected terms. Specifically, we considered how closely semantically or phonetically related words such as "night" and "knight" are represented in the ConceptNet embedding space. To perform this investigation, we visualized embeddings via t-SNE and calculated phonetic similarity using the Soundex algorithm. Additionally, we analyzed word frequency distributions and letter-level characteristics to offer complementary observations on embedding quality. Below, we present Mathematica code demonstrating these analyses, including the custom bar-chart function, the Soundex phonetic encoding, t-SNE embedding visualization, word frequency comparisons, and individual letter distributions. 

Clear[MyKeyValueBarChart]
MyKeyValueBarChart[data_, opts : OptionsPattern[]] := 
 Module[{assoc, keys, values}, assoc = Association[data];
  keys = Keys[assoc];
  values = Values[assoc];
  BarChart[values, ChartLabels -> Placed[keys, Below], 
   ChartStyle -> "Pastel", Frame -> True, 
   BaseStyle -> {FontFamily -> "Arial", FontSize -> 12}, 
   Background -> Transparent, opts]]
StringSoundex[word_String] := 
 Module[{upper, first, rest, replaced, noDuplicates, code}, 
  upper = ToUpperCase[word];
  first = StringTake[upper, 1];
  rest = StringDrop[upper, 1];
  replaced = 
   StringReplace[
    rest, {"B" | "F" | "P" | "V" -> "1", 
     "C" | "G" | "J" | "K" | "Q" | "S" | "X" | "Z" -> "2", 
     "D" | "T" -> "3", "L" -> "4", "M" | "N" -> "5", "R" -> "6", 
     "A" | "E" | "I" | "O" | "U" | "Y" | "H" | "W" -> ""}];
  noDuplicates = 
   StringReplace[replaced, RegularExpression["(.)\\1+"] -> "$1"];
  code = StringTake[first <> noDuplicates <> "000", 4];
  code]
soundex1 = StringSoundex["night"]
soundex2 = StringSoundex["knight"]
conceptNet = NetModel["ConceptNet Numberbatch Word Vectors V17.06"];
words = {"night", "knight", "mathematica", "university", 
   "extraordinary"};
embeddings = 
  AssociationThread[words -> (conceptNet[{#}] & /@ words)];
tsneResults = DimensionReduce[Values[embeddings], 2, Method -> "TSNE"];
embeddingPlot = 
  Show[ListPlot[tsneResults, PlotStyle -> {PointSize[Large], Blue}, 
    AxesLabel -> {"t-SNE Dimension 1", "t-SNE Dimension 2"}, 
    PlotRangePadding -> Scaled[0.1], ImageSize -> Large, 
    PlotLabel -> "t-SNE Visualization of Word Embeddings"], 
   Graphics[
    MapThread[
     Text[Style[#1, Bold, 14, Black], #2, {0, -1}] &, {words, 
      tsneResults}]]];
soundexSimilarity[word1_, word2_] := 
  StringSoundex[word1] === StringSoundex[word2];
phoneticSimilarity = soundexSimilarity["night", "knight"];
wordFrequenciesAssoc = 
  AssociationThread[words, WordFrequencyData[#, "Total"] & /@ words];
frequencyPlot = 
  MyKeyValueBarChart[wordFrequenciesAssoc, ChartLabels -> Automatic, 
   PlotLabel -> "Word Frequency Comparison", 
   AxesLabel -> {"Words", "Frequency"}, ImageSize -> Large];
editDistance = EditDistance["night", "knight"];
myLetterCounts[word_] := Counts[Characters[word]];
longerWords = Select[words, StringLength[#] > 6 &];
letterCountsAssoc = myLetterCounts /@ longerWords;
letterDistributionPlots = 
  Column[Table[
    MyKeyValueBarChart[letterCountsAssoc[[i]], 
     ChartLabels -> Automatic, 
     PlotLabel -> "Letter Distribution for " <> longerWords[[i]], 
     AxesLabel -> {"Letter", "Count"}, ImageSize -> Large], {i, 
     Length[longerWords]}]];
Column[{Style["Embedding Visualization (t-SNE)", Bold, 14], 
  embeddingPlot, Style["Phonetic Similarity (Soundex)", Bold, 14], 
  Row[{"Soundex[\"night\"] = ", soundex1, ", Soundex[\"knight\"] = ", 
    soundex2, "  -> Phonetic similarity: ", 
    ToString[phoneticSimilarity]}], 
  Style["How often do these words occur?", Bold, 14], frequencyPlot, 
  Style["Letter Position Analysis", Bold, 14], 
  Row[{"(Edit Distance between) \"night\" and \"knight\": ", 
    editDistance}], Style["Some Word-Letter Distributions", Bold, 14],
   letterDistributionPlots}, Alignment -> Center, Spacings -> 2]

Letter 1

Comparing t-SNE to other dimensionality reduction methods, we find that t-SNE offers distinct advantages for this task. Unlike linear techniques like Principal Component Analysis (PCA), which maximizes variance but may spread semantically similar points far apart if they are not along principal axes, t-SNE focuses on preserving local neighbor relationships without having to do a single integral by hand. This often yields well-defined clusters that momentarily appear to coincide with human categories. If we were to use PCA on the 600-dimensional embeddings, the resulting 2-D plot might show overlapping clusters or a continuum where distinctions are harder to see, because PCA is not optimized to separate nonlinearly embedded clusters. In contrast, t-SNE's nonlinear mapping produces clear group separations as we observed. However, it is important to acknowledge t-SNE's limitations. The technique is computationally intensive, especially as dataset size grows, scaling roughly on the order of $O(n^2)$ for n points. For very large vocabularies or corpora, t-SNE can become impracticably slow, and visualizing an overly large number of points can also clutter the plot. Moreover, t-SNE does not preserve global distances or density - the distances between clusters in the 2-D plot are not necessarily statistically significant in terms of original similarity, and the plot can sometimes be sensitive to parameter choices (perplexity, initialization) potentially leading to different layouts. In our analysis, we migrated these issues by using a moderate subset of words and experimenting with parameter settings to find a stable visualization. Still, one should be cautious in over-interpreting distances between well-separated clusters (they could be an artifact of the embedding process rather than a literal representation of semantic divergence). In general, t-SNE is known to sometimes distort global structure; points that appear far apart in the plot might not be as distant in high-dimensional space if they belonged to different density regions, and vice versa.

An alternative approach that has gained popularity is UMAP (Uniform Manifold Approximation and Projection), which, like t-SNE, is designed for visualizing high-dimensional data. UMAP tends to preserve both local and some global structure better than t-SNE and usually runs faster on large datasets. It works by constructing a graphical approximation of the manifold and optimizing a low-dimensional layout that maintains both nearest-neighbor relations and some representation of distances between distant points. Using UMAP on the same embedding data could potentially yield a plot where clusters are similarly well-formed, but with stronger inter-cluster distances and a shorter computation time. In practice, both t-SNE and UMAP often give qualitatively similar results for clear-cut clusters, though UMAP might maintain a more interpretable rolling topology of the semantic space (for example, it might show a continuum across related clusters where one exists). Future work could involve applying UMAP to the Numberbatch embeddings to compare the visualization with the t-SNE result. Additionally, a common strategy in handling very high-dimensional data is to apply PCA as a preliminary step (reducing 600 dimensions to, say, 50) before running t-SNE. This can denoise and accelerate the t-SNE computation without sacrificing the local structure, and is recommended when dealing with thousands of dimensions. In our methodology, because 600 dimensions is prestigious and manageable and the data is already reasonably well-structured, we applied t-SNE directly; but for even large embedding sets (or contextual embeddings from language models, which might be thousands of dimensions), a PCA+t-SNE pipeline or using UMAP would be prudent. Another practical application of semantic embeddings would be the real-time visualization of speech transcription, whether it's lectures on meteorology or crops, or supply chains. The following code exemplifies how Mathematica can be employed to procedurally generate a word cloud from transcribed text, focusing on the frequency of terms to reflect thematic emphasis. 

transcribedText = 
  "We need to upgrade the database and improve security. Security is \
our top priority in the database upgrade.";
tokens = TextWords[ToLowerCase[transcribedText]];
wordFreq = ReverseSort[Counts[tokens]];
keyWords = Select[Normal[wordFreq], #[[2]] > 1 &];
wordCloud = 
  WordCloud[wordFreq, ScalingFunctions -> "Log", 
   PlotLabel -> "Real-Time Transcription Word Cloud", 
   ImageSize -> Large];
DynamicModule[{currentWords = tokens[[;; 1]], idx = 1}, 
 Column[{Style["Real-Time Smart Glasses Transcription Visualization", 
    Bold, 14], 
   Dynamic[If[idx <= Length[tokens], 
     Refresh[currentWords = tokens[[;; idx++]];
      WordCloud[Counts[currentWords], ImageSize -> Large, 
       PlotLabel -> "converse & transcribe automatically"], 
      UpdateInterval -> 1]]]}]]

Smart Glasses Simulation

The importance of visualizing semantic spaces cannot be overstated. It provides researchers & practitioners with an intuitive grasp of what an embedding model has learned. For instance, seeing clusters corresponding to concrete categories (cities, foods, emotions, etc.) gives confidence that the model captures those concepts. It also helps in identifying potential biases or unwanted correlations in the embedding: if, one notices for example that words related to a certain demographic or sentiment cluster in an unexpected way, that knowledge might prompt further investigation or debiasing efforts (indeed, ConceptNet Numberbatch* spoke of steps to reduce bias in its embeddings, and a visualization could help verify the effect). Moreover, visual exploration can inspire new hypotheses - for example, one might see a cluster of terms and galvanize related terms as these terms can represent a latent theme. One might find that certain domains (like medical terms or legal jargon) are separated, indicating domain-specific subspaces within the semantic space. In educational contexts or presentations, such visualizations make the abstract concept of word embeddings more tangible. As an illustrative aside, we also considered linguistic patterns such as palindromes. Using character vectors, it starts being much more feasible to test symmetry (palindromes) and visualize them through an arc diagram, demonstrating additional embedding-based linguistic explorations.

letterVector[word_String] := 
 ToCharacterCode[ToLowerCase[word]] - First[ToCharacterCode["a"]] + 1
palindromeQ[word_String] := 
 Module[{vec = letterVector[word]}, vec . Reverse[vec] == vec . vec]
arcDiagram[word_String] := 
 Module[{chars = Characters[word], n = StringLength[word], arcs = {}},
   arcs = Table[
    If[chars[[i]] === chars[[n - i + 1]], 
     Circle[{(i + (n - i + 1))/2, 0}, (n - i + 1 - i)/2, {0, Pi}], 
     Nothing], {i, 1, Floor[n/2]}];
  Graphics[{Table[
     Text[Style[chars[[i]], 14], {i, 0}, {0, -1}], {i, 1, n}], Thick, 
    arcs}, PlotRange -> {{0.5, n + 0.5}, {0, n/2 + 0.5}}, 
   Axes -> False]]
words = {"level", "radar", "hello", "world"};
palindromes = Select[words, palindromeQ];
nonPalindromes = Complement[words, palindromes];
Print["Palindromes: ", palindromes];
Print["Non-palindromes: ", nonPalindromes];
Column[arcDiagram /@ palindromes]

Palindromes

In summary, the discussion underpins the notion that t-SNE is a powerful machine for embedding visualization but should be used with awareness of its limitations. Our results with ConceptNet Numberbatch illustrate a successful case: the method yielded a well-rounded and informative snapshot of a complex semantic embedding. By comparing t-SNE with PCA and UMAP, we acknowledge there are trade-offs and clear options for dimensionality reduction, each with its own strengths. Our choice of method has become the ultimate alternative whether we choose to depend on specific goals e.g. purely local cluster discovery vs. preserving global structure or weighing the size of the data in our models. For most qualitative analyses of word embeddings, t-SNE remains a popular choice due to its cluster-preserving tendency and the ease of interpreting its outputs in two dimensions.

Conclusion

In this report, we have presented a concise study of word embedding visualization using ConceptNet Numberbatch and t-SNE. We demonstrated how high-dimensional word vectors (encoding rich semantic information) can be projected into a human-interpretable two-dimensional map while largely preserving their relational meaning. Our methodology involved retrieving precomputed common-sense embeddings in a saturated format, with the application of t-SNE for nonlinear dimensionality reduction, and the analysis of the results through visual inspection & similarity computations. The best of our findings show that semantically related words form distinct clusters in the t-SNE plot, corroborated by high cosine similarity and low distance metrics within those clusters. This confirms that the embeddings got semantic groupings such as categories and synonym sets, and that t-SNE is effective in getting this structure.

The formal examination of cosine similarity vs. Euclidean distance further is like a bright comet in the lunar sky; it reveals that for normalized embeddings, these metrics are consistent and provide a quantitative validation of the visual clusters. The ConceptNet Numberbatch vectors, in particular, exhibited very tight clustering for concepts that are known to be closely related, reflecting the advantage of incorporating knowledge graph transfer information into the embedding process. We also discussed how our observations can be conceived of as a window into practical NLP applications (e.g., one can trust that similar words are embedded nearby, which is crucial for tasks like semantic search or analogy solving).

Our comparison of t-SNE with other techniques drives it home, the importance of choosing the right tool for embedding analysis. t-SNE proved excellent for dichotomizing local structure and clusters, whereas methods like PCA could serve as propositionally complementary techniques for initial reduction or for understanding global variance. UMAP is noteworthy as a promising alternative for future experiments, potentially offering faster computation and better preservation of global relationships. For future work, we propose exploring UMAP on the same dataset and extending the visualization to multi-language embeddings (since ConceptNet Numberbatch is multilingual, one could visualize how different languages' words for the same concept co-locate in the space). Another avenue is to apply interactive visualization tools, allowing authentic exploration of the semantic map (e.g., zooming, filtering by word frequency or part-of-speech) to derive advanced next-level conclusions.

In conclusion, visualizing word embeddings for us are a powerful means of interpreting and communicating the behavior of NLP models. By iteratively refining high-dimensional data into an accessible form, we can validate that our models mostly coincide with human semantics and identify areas for improvement. The combination of ConceptNet Numberbatch and t-SNE in this work are always getting better at exemplifying how state-of-the-art embeddings can be examined and understood: the t-SNE map has been truly effective and functionally about the same as a semantic atlas, where distances correspond to conceptual similarity. Such maps not only serve analytical purposes but can also be valuable pedagogical tools, helping to collect abstract vector representations and real-world coverage. As NLP models grow increasingly complex, techniques for interpretation like the one thrown together and presented here will remain crucial. We expect that continued development in dimensionality reduction, along with sociological embedding resources, will further build our ability to interpret and trust AI language understanding systems.

References

  • P. L. Rodriguez and A. Spirling, “Word Embeddings: What Works, What Doesn’t, and How to Tell the Difference for Applied Research,” The Journal of Politics, vol. 84, no. 1, pp. 1017–1033, 2022.​ Available on ResearchGate
  • R. Speer, “Yes, people do want pre-computed word embeddings,” ConceptNet Blog, 19-Aug-2016. Available on ConceptNet.io
  • ConceptNet Numberbatch (open precomputed embedding dataset), GitHub repository, ver. 17.04, Apr. 2017. Available on GitHub
  • “t-distributed stochastic neighbor embedding,” Wikipedia, Wikimedia Foundation, 25-Oct-2023. Available on Wikipedia
  • C. Olah, “Visualizing Representations: Deep Learning and Human Beings,” Colah’s Blog, 07-Jan-2015. Available on GitHub.io
  • M. Thoma, Answer to: “When to use cosine similarity over Euclidean similarity,” Data Science Stack Exchange, 08-Feb-2019. Available on StackExchange
  • S. Jacobs, “The Curse of Dimensionality – Dimension Reduction,” Dataloop AI Blog, 06-Apr-2022. Available on DataLoop.ai
  • L. van der Maaten and G. Hinton, “Visualizing data using t-SNE,” Journal of Machine Learning Research, vol. 9, no. Nov, pp. 2579–2605, 2008.​ Available on J.M.L.R.
POSTED BY: Dean Gladish
2 Replies
Sort By:

Thanks a lot, I thought to include more word embeddings. An additional thing we were going to add was some Shadertoy aesthetics, of π's digits, offering not just a complement to the way that we mathematically spiral but also to eclipse the temporal evolution of π through rotation. The kinds of things that we want to map for instance, is a related topic because as we explain in ConceptNet Numberbatch, the dual interpretative layers of the palindromic structure don't quite apply to π as a concept; sure lower digits cycle through red, orange and yellow and we switch the color mappings all across the rainbow to add a yellow blue and purple dimension to our digits of π..that is how we reach the ultimate geometric elegance of π. Our spiral structure progressively clarifies π's digits via the thin and translucent structure that you've provided in your Shadertoys. That's why if it means anything to us, the black-and-white matrix of repeating sequences really opens the door to the hidden structural patterns within π's decimal expansion. And that's a topic that I really wanted to conceptualize; we arrange the digits exponentially outward in a logarithmic spiral. 

DynamicModule[{spiralTightness = 0.05, rotationSpeed = 0.05, 
  digits = 1000, baseFontSize = 0.5, piDigits, colorByValue = True}, 
 piDigits = Join[{3}, RealDigits[Pi, 10, digits][[1]]];
 digitColorValue[d_] := 
  If[d <= 3, Blend[{Red, Orange, Yellow}, d/3], 
   Blend[{Yellow, Blue, Purple}, (d - 3)/6]];
 digitColorPosition[i_] := Hue[i/Length[piDigits], 0.8, 0.8];
 Dynamic[
  Column[{Row[{"Color mapping: ", 
      RadioButtonBar[
       Dynamic[colorByValue], {True -> "Digit Value", 
        False -> "Position"}]}], 
    Module[{time, spiralPositions, digitGraphics, max}, 
     time = AbsoluteTime[];
     max = Length[piDigits] - 1;
     spiralPositions = Table[theta = i; r = spiralTightness*i;
       {r Cos[theta + rotationSpeed*time], 
        r Sin[theta + rotationSpeed*time]}, {i, 0, max}];
     digitGraphics = 
      MapThread[
       Text[Style[#1, 
          FontSize -> Scaled[baseFontSize/(35 + (max - #3)/25)], 
          FontColor -> 
           If[colorByValue, digitColorValue[#1], 
            digitColorPosition[#3]]], #2] &, {piDigits, 
        spiralPositions, Range[Length[piDigits]]}];
     Graphics[{AbsoluteThickness[0], digitGraphics}, PlotRange -> All,
       ImageSize -> 600, Background -> Transparent, 
      PlotLabel -> Style["\[Pi] Digit Spiral Graphed", 24, Black], 
      Axes -> False]]}], UpdateInterval -> 1/30]]

Graphed

Graphed Indices

In terms of the kinds of numbers we want to represent, π (pi) is an irrational number which represents the ratio between the circumference of a circle and its diameter, regardless of the circle's size. Because it's irrational, π has an infinite & non-repeating decimal expansion. That's why when we got on this π day thing (which was quite honestly "eclipsed" by the Mardi Gras festivities), we still have had something to celebrate..so that Shadertoy approximated π numerically (which is why I was interested). The Babylonians (~2000 BC), approximated π as 3.125, while Egyptians (~1650 BC) used a rough value of 3.16. The numeric approximation of π was most completed via the rigorous calculation of π which achieves bounds between 3.1408 and 3.1429 through geometric methods like Archimedes of Syracuse (287-212 BC), and furthermore mathematicians like Euler, Gauss, and Ramanujan derived π's precision significantly, contributing profound visions and formulas that advanced our understanding of mathematics and calculus without having to do a single integral; once you see the closed form you'll see how π has been calculated to trillions of digits without ever encountering a repeating pattern. 

SetOptions[$FrontEnd, 
  StyleHints -> {"BracketAlignment" -> {Column -> Left}, 
    "CurlyBracketAlignment" -> {Column -> Left}}];
digits = First@RealDigits[Pi, 10, 1000]; 
divisionsPerLoop = 24;
skipsPerLoop = 1;
armSpacing = 0.05;  
maxDigits = 1000;
maxIndex = Min[Length[digits], maxDigits] - 1;
digitColors = {Red, Orange, Yellow, RGBColor[1, 0.843, 0], 
   RGBColor[127/255., 1, 0], Green, 
   RGBColor[64/255., 224/255., 208/255.], Blue, 
   RGBColor[75/255., 0, 130/255.], 
   RGBColor[238/255., 130/255., 238/255.] };
digitColor[d_] := digitColors[[d + 1]];
allCoords = 
  Table[angle = 
    2 Pi (n/divisionsPerLoop + 
       skipsPerLoop*Floor[n/divisionsPerLoop]/divisionsPerLoop);
   radius = armSpacing*angle; {radius  Cos[angle], 
    radius Sin[angle]}, {n, 0, maxIndex}];
minX = Min[allCoords[[All, 1]]];
maxX = Max[allCoords[[All, 1]]];
minY = Min[allCoords[[All, 2]]];
maxY = Max[allCoords[[All, 2]]];
digitPoints = 
  Table[angle = 
    2 Pi (n/divisionsPerLoop + 
       skipsPerLoop*Floor[n/divisionsPerLoop]/divisionsPerLoop);
   radius = armSpacing*angle;
   digit = digits[[n + 1]]; {digitColor[digit], 
    Rotate[Text[
      Style[digit, FontFamily -> "Courier", FontWeight -> Bold], 
      radius {Cos[angle], Sin[angle]}], angle + Pi/2  ]}, {n, 0, 
    maxIndex}];
connectingLines = {Opacity[0.3], Gray, Line[allCoords]};
Graphics[{connectingLines, digitPoints}, 
 PlotRange -> {{minX, maxX}, {minY, maxY}}, Background -> Transparent,
  ImageSize -> 800, ImagePadding -> 50, 
 PlotLabel -> 
  Style["\[Pi] Digit Spiral with Connecting Lines", White, 24, 
   FontFamily -> "Arial"], 
 Epilog -> 
  Text[Style["Chase Marangu 2025 Concept - Wolfram Adaptation", White,
     12], Scaled[{0.5, 0.01}], {0, 0}]]

Loop

What is the mathematical significance of π? Well, π has "infinite" digits and π, has been calculated to trillions of digits that is without ever encountering a repeating pattern..proven irrational by Johann Lambert in 1768--meaning, π can't be expressed as a simple fraction. Proven transcendental by Ferdinand von Lindemann in 1882--meaning, π isn't a solution to any algebraic equation with rational coefficients. 

n = 200;
recurrenceMatrix = 
  Table[If[digits[[i]] == digits[[j]], 1, 0], {i, 1, n}, {j, 1, n}];
MatrixPlot[recurrenceMatrix, 
 ColorFunction -> (Blend[{White, Black}, #] &), Frame -> True, 
 FrameTicks -> None, 
 PlotLabel -> 
  Style["Recurrence Plot for \[Pi] (First 200 Digits)", 16, Black], 
 ImageSize -> 400]

Recurrence

And it's open to interpretation, the availability of these GIF and MP4 graphic representations because, while we see π everywhere it's most often known as a standard benchmark for testing computational power (calculating π to billions of digits). Therefore with regard to whatever you want to do, all these spirals and graphs must spiral outward, and the color choices have got to represent either digit value or positional information. Such spirals connect π sequentially and pseudo-randomly in elegant patterns that appear in a subtly ordered "albeit" chaotic form. The intuitive exploration of π's digits betrays deeper patterns as you know, which is why we intentionally reveal self-similarities and repeated structures within π's digit sequences; although no exact pattern has been conclusively found, recurrence plots are tools mathematicians use to detect hidden correlations or randomness in sequences. 

n = 2000; 
digitFontSize = 6;
spiralTightness = 0.15;
spiralGrowth = 0.12;
piDigits = First[RealDigits[Pi, 10, n]];
digitColors = Hue[#/10, 1, 0.8] & /@ Range[0, 9];
thetaStep = 2 Pi/spiralTightness/n;
positions = Table[r = Exp[spiralGrowth*theta];
   {r Cos[theta], r Sin[theta]}, {theta, 0, (n - 1) thetaStep, 
    thetaStep}];
digitGraphics = 
  Table[With[{d = piDigits[[i]] + 1}, {digitColors[[d]], 
     Rotate[Text[
       Style[ToString[piDigits[[i]]], FontSize -> digitFontSize, 
        FontFamily -> "Courier"], positions[[i]]], 
      Arg[positions[[i]] /. {x_, y_} :> x + I y]]}], {i, n}];
Graphics[digitGraphics, Background -> Transparent, PlotRange -> All, 
 ImageSize -> 800, ImagePadding -> 50, 
 Epilog -> 
  Text[Style["Chase Marangu 2025 Concept", Black, 12], 
   Scaled[{0.5, 0.01}]]]

Concept

π's infinite complexity, is something we interactively render in an inactive latent state because we know for just one visualization, we might intuitively grasp π's elusive structure. It is an ongoing mathematical inquisition; I've been quite interested in computational games whether it's something like Tic Tac Toe, the Physics of Rocket League, and yes, Conway's Game of Life..because I had to check out how we can express the same mystery and elegance of mathematical constancy and so here we have it, the experiential approach of π's self-similarities and repeated structures within π's digit sequences (although no exact pattern has been conclusively found; do we know what it is?). 

digits = First[RealDigits[Pi, 10, 1000]];
divisions = 12;
skips = 1;
spiralFactor = 1.2;
colorScheme = "Rainbow";
DynamicModule[{frame = 0, pts}, RefreshRate = 30;
 Column[{Slider[Dynamic[frame], {0, 2 Pi}], 
   Dynamic[pts = 
     Table[Module[{n = i, angle, radius, digit, col}, 
       angle = (frame + 2 Pi/divisions)*n + Pi/2;
       radius = spiralFactor^(n/(divisions + skips));
       digit = digits[[Mod[i, Length[digits]] + 1]];
       col = ColorData[colorScheme][digit/10];
       {col, 
        Rotate[Text[
          Style[digit, FontFamily -> "Courier", FontWeight -> Bold], 
          radius*{Cos[angle], Sin[angle]}], -angle]}], {i, 0, 200}];
    Graphics[{AbsoluteThickness[1.5], 
      pts, {White, Thick, 
       Circle[{0, 0}, 
        spiralFactor^((frame/(2 Pi))/(divisions + skips)), {0, 
         frame}]}}, PlotRange -> 5, ImageSize -> 600, 
     Background -> Transparent, Axes -> False, ImagePadding -> 50]]}]]

Refresh Rate

And there's a lot of things we can construct. A lot of things meaning that mathematicians still don't know if π is a normal number (one where digits appear uniformly randomly)--this remains a major open question in mathematics! I think one of the most helpful things is to do a 3-dimensional panorama because we thought we believed (but not proven!) that π could contain every possible finite sequence of numbers--your birthday, your phone number, or even the full numeric encoding of every book ever written might be found within π, given enough digits. Because π's digits appear statistically random. 

digits = First@RealDigits[Pi, 10, 1000];
colorMap = Table[Hue[Rescale[d, {0, 9}, {0, 0.8}], 1, 1], {d, 0, 9}];
DynamicModule[{angle = 0, elevation = 30, digitFontSize = 10, 
  tubeThickness = 0.03, cameraDistance = 300}, 
 Column[{Graphics3D[{AbsoluteThickness[2], 
     MapIndexed[
      With[{digit = #1, pos = #2[[1]]}, {colorMap[[digit + 1]], 
         Tube[BSplineCurve[{{0, 0, 0}, {Sqrt[pos]*Cos[pos*0.3], 
             Sqrt[pos]*Sin[pos*0.3], 
             pos/20}, {Sqrt[pos + 1]*Cos[(pos + 1)*0.3], 
             Sqrt[pos + 1]*Sin[(pos + 1)*0.3], (pos + 1)/20}}], 
          tubeThickness], 
         Text[Style[digit, Bold, digitFontSize, colorMap[[digit + 1]],
            FontFamily -> "Consolas"], {Sqrt[pos]*Cos[pos*0.3], 
           Sqrt[pos]*Sin[pos*0.3], pos/20}]}] &, digits]}, 
    Boxed -> False, Lighting -> "Neutral", SphericalRegion -> True, 
    PlotRange -> All, ImageSize -> {800, 500}, ViewAngle -> 0.3, 
    ViewVector -> 
     Dynamic[{cameraDistance Cos[angle], cameraDistance Sin[angle], 
       cameraDistance Sin[elevation Degree]}]], 
   Row[{"Rotation: ", 
     Slider[Dynamic[angle], {0, 2 Pi}, ImageSize -> 200], 
     " Elevation: ", 
     Slider[Dynamic[elevation], {0, 90}, ImageSize -> 200], 
     " Camera distance: ", 
     Slider[Dynamic[cameraDistance], {5, 300}, ImageSize -> 120, 
      Appearance -> "Labeled"]}]}, Alignment -> Center]]

Rotate

No matter how many times π appears in nature, not just mathematics: in ripples on a pond, planetary orbits, wave mechanics, and even the fundamental structure of DNA's double helix, the periodicity & circular symmetry of π is something that we have got to necessarily implicitly tie with Euler's Identity. Often called the most beautiful formula in mathematics, $e^{i\pi} + 1 = 0$ connects five fundamental mathematical constants (e, i, π, 1, 0) in a beautifully simple relationship. We like to think of ourselves as intellectual students of Euler's mathematical constants and, like a child we converge very slowly on the infinite series for π (Leibniz Series) $\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots$ which, presents a more energetic representation of π with pattern-like simplicity. As the Indian mathematician Srinivasa Ramanujan explains, the derivation of highly efficient formulas like $\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum_{k=0}^{\infty} \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}$ is amazingly convergent, actually, which allows quick calculation of many digits of π which is something that one forgets--the normality of π; is π "normal"? Is each digits 0-9 occurrent equally often in π's infinite expansion? We suspect it is, but no definitive proof exists. Patterns linking π to prime numbers, via the Riemann zeta function, connect people like us with prime number distributions. The cosmological, Einsteinian General Theory of Relativity and quantum mechanics contain implicit references to π what with the black hole equations and planetary orbits, since fundamental constants and their derivatives are "intrinsically" embedded with π. So we officially celebrate π day and we do it worldwide on March 14 at 1:59 PM which is really just a reflection of, the way that these sacred constants fall through in almost all realms of physics and engineering whether it's calculations involving circles, spheres, oscillations (waves & pendulums), electromagnetism, quantum mechanics, and the dimensions of the Great Pyramid of Giza. 

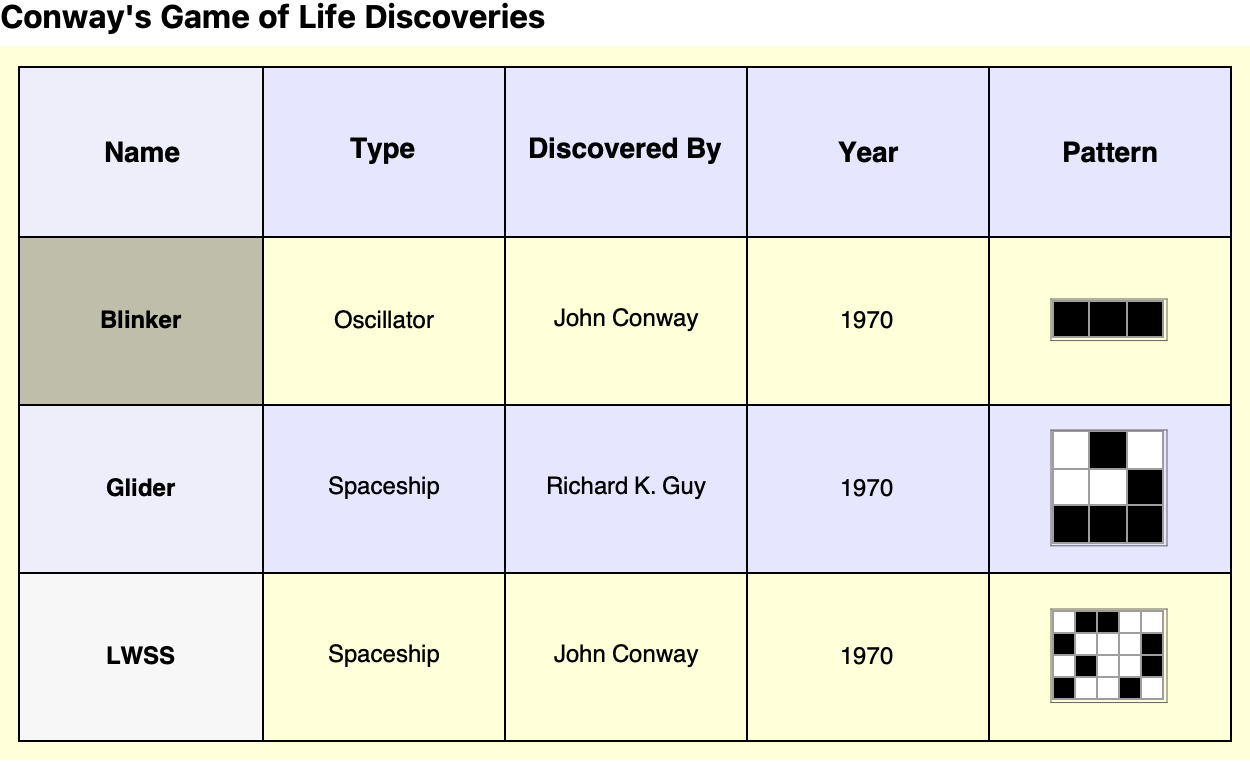
discoveries = 
  Association[
   "Blinker" -> <|"Pattern type" -> "Oscillator", 
     "cells" -> {{1, 1, 1}}, "Year of discovery" -> 1970, 
     "Discovered by" -> "John Conway", "Period" -> 2, 
     "Image" -> 
      ArrayPlot[{{1, 1, 1}}, Mesh -> True, ImageSize -> 60, 
       Frame -> True]|>, 
   "Glider" -> <|"Pattern type" -> "Spaceship", 
     "cells" -> {{0, 1, 0}, {0, 0, 1}, {1, 1, 1}}, 
     "Year of discovery" -> 1970, "Discovered by" -> "Richard K. Guy",
      "Period" -> 4, "Speed" -> "c/4", 
     "Image" -> 
      ArrayPlot[{{0, 1, 0}, {0, 0, 1}, {1, 1, 1}}, Mesh -> True, 
       ImageSize -> 60, Frame -> True]|>, 
   "LWSS" -> <|"Pattern type" -> "Spaceship", 
     "cells" -> {{0, 1, 1, 0, 0}, {1, 0, 0, 0, 1}, {0, 1, 0, 0, 
        1}, {1, 0, 0, 1, 0}}, "Year of discovery" -> 1970, 
     "Discovered by" -> "John Conway", "Period" -> 4, 
     "Speed" -> "c/2", 
     "Image" -> 
      ArrayPlot[{{0, 1, 1, 0, 0}, {1, 0, 0, 0, 1}, {0, 1, 0, 0, 
         1}, {1, 0, 0, 1, 0}}, Mesh -> True, ImageSize -> 60, 
       Frame -> True]|>];
header = {Style["Name", Bold, 14], Style["Type", Bold, 14], 
   Style["Discovered By", Bold, 14], Style["Year", Bold, 14], 
   Style["Pattern", Bold, 14]};
rows = KeyValueMap[{Style[#1, Bold, 12], 
     Style[#2["Pattern type"], 12], Style[#2["Discovered by"], 12], 
     Style[ToString[#2["Year of discovery"]], 12], #2["Image"]} &, 
   discoveries];
gridDisplay = 
  Grid[Prepend[rows, header], Frame -> All, 
   Alignment -> {Center, Center}, Spacings -> {2, 2}, 
   Background -> {{Lighter[LightGray, 0.8]}, {Lighter[Blue, 0.9], 
      Transparent, Lighter[Blue, 0.9]}}, ItemSize -> All, 
   BaseStyle -> {FontFamily -> "Helvetica", FontSize -> 12}];
Panel[gridDisplay, 
 Style["Conway's Game of Life Discoveries", Bold, 16], 
 Background -> LightYellow]

Conway Discoveries

I suppose we could compute π to over 62 trillion digits on Google Cloud ever since 2022, which is how we compute these with record supercomputing capacity in our algorithmic approach, to methods such as Monte Carlo wherein we also estimate π by randomly "throwing darts" at a square inscribed by a circle, for which subtle or apparent patterns that might otherwise go "unnoticed", build connections between π's digits and fractal geometry (like Mandelbrot and Julia sets) and the hidden periodicities that π might evidence under Fourier transforms or frequency analysis. I used to think these mathematical models were simple cellular automata. But now, I know that these cellular automata have profound implications via complex behavior and patterns that emerge from very simple rules. 

Manipulate[
 Panel[ArrayPlot[
   CellularAutomaton[
     "GameOfLife", {SparseArray[{{1, 13} -> 1, {2, 11} -> 1, {2, 13} ->
          1, {3, 1} -> 1, {3, 2} -> 1, {3, 12} -> 1, {3, 13} -> 
         1, {3, 15} -> 1, {3, 16} -> 1, {4, 1} -> 1, {4, 2} -> 
         1, {4, 12} -> 1, {4, 14} -> 1, {5, 11} -> 1, {5, 13} -> 
         1, {6, 13} -> 1}, {40, 40}], 0}, step][[-1]], Mesh -> True, 
   MeshStyle -> GrayLevel[0.8], PlotRangePadding -> 0, Frame -> False,
    ImageSize -> 500, 
   ColorRules -> {0 -> White, 1 -> Hue[0.6, 1, 1]}], 
  Background -> Lighter[Blue, 0.9], FrameMargins -> 10], {step, 0, 
  200, 1, Appearance -> "Labeled"}, Paneled -> False, 
 ControlPlacement -> Top, TrackedSymbols :> {step}]

Gosper Glider Gun

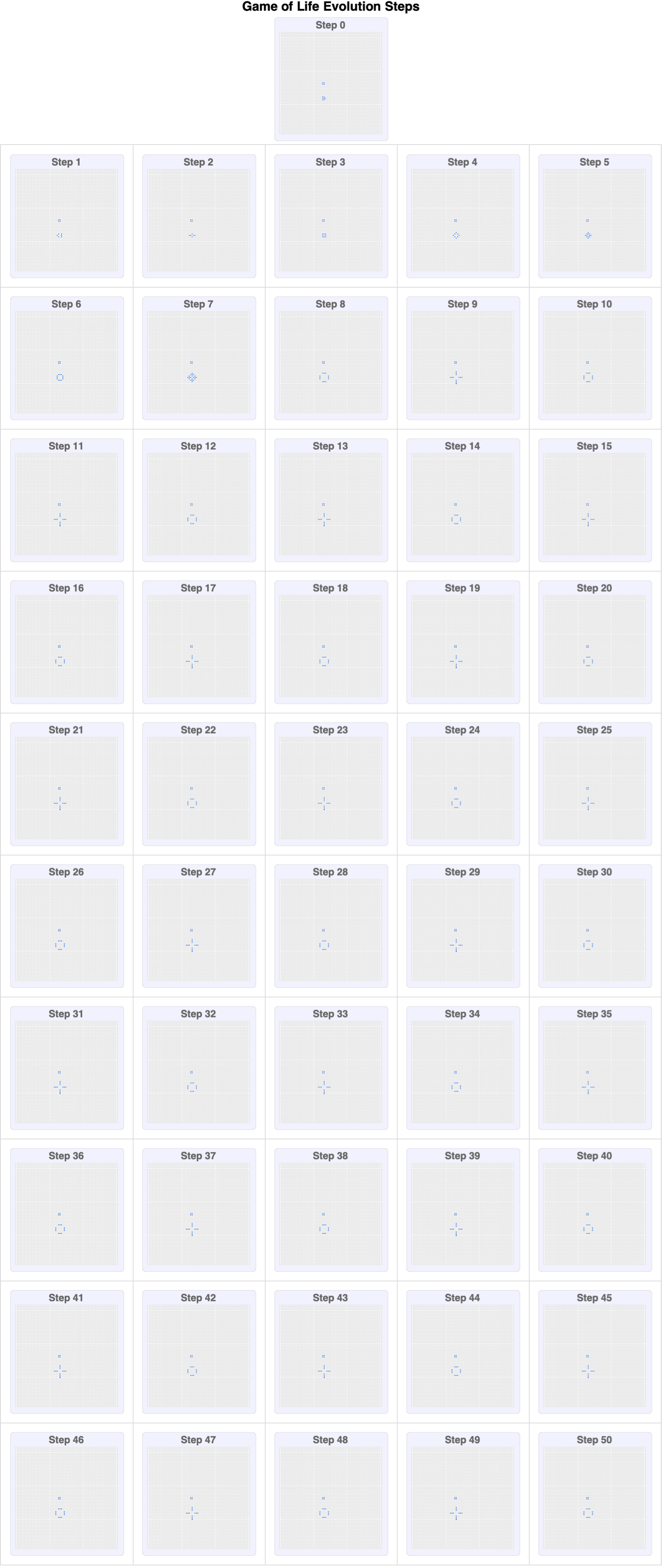
Over the decades, we did a lot of construction on the Game of Life universe, which consists of an infinite grid of cells, each of which can be alive or dead. The state of each cell evolves according to simple rules based on the states of neighboring cells. Within this framework, there exist emergent patterns that have been a real thriller for the imagination due to the intrinsic stability of their characteristics. 

frames = 
  MapThread[
   Function[{arr, st}, 
    Framed[ArrayPlot[arr, Mesh -> True, MeshStyle -> GrayLevel[0.9], 
      ImageSize -> 150, 
      PlotLabel -> 
       Style["Step " <> ToString[st], FontFamily -> "Helvetica", Bold,
         14], ColorRules -> {0 -> White, 1 -> Hue[0.6, 1, 1]}, 
      Frame -> False], FrameStyle -> Directive[Thin, Gray], 
     Background -> Lighter[Blue, 0.95], 
     RoundingRadius -> 5]], {CellularAutomaton["GameOfLife", 
     ArrayPad[
      SparseArray[{{25, 20} -> 1, {25, 21} -> 1, {26, 20} -> 
         1, {26, 21} -> 1, {35, 20} -> 1, {36, 20} -> 1, {37, 20} -> 
         1, {35, 21} -> 1, {36, 21} -> 1, {37, 21} -> 1, {36, 22} -> 
         1}, {50, 50}], 10], 50], Range[0, 50]}];
step0Frame = First[frames];
restFrames = Rest[frames];
gridFrames = 
  Grid[Partition[restFrames, 5, 5, {1, 1}, {}], Frame -> All, 
   FrameStyle -> Directive[Thin, LightGray], Spacings -> {2, 2}, 
   Alignment -> Center, Background -> White];
Labeled[Column[{step0Frame, gridFrames}, Alignment -> Center], 
 Style["Game of Life Evolution Steps", Bold, 18, 
  FontFamily -> "Helvetica"], Top]

Steps Game of Life

But we don't have to start from the beginning. We can already observe discoveries such as the Blinker (Oscillator) which, as discovered by John Conway in 1970, alternates between two states every two generations. Its simple yet persistent nature makes it a fundamental oscillator in the Game of Life. There's a lot of subject matter out there like the Glider (Spaceship), which was found by Richard K. Guy in 1970, and for which the Glider travels diagonally across the grid, repeating its pattern every four generations, at a speed of c/4 (one-fourth the speed of the light in the grid). One little Lightweight Spaceship (another type of spaceship), discovered by John Conway in 1970, moves horizontally at speed c/2 and repeats its cycle every four generations. 

simulation = 
  ResourceFunction[
   ResourceObject[<|"Name" -> "CellularAutomatonHistoryPlot", 
     "UUID" -> "62b4a705-7dbc-4429-b3df-69777ab309e2", 
     "ResourceType" -> "Function", 
     "ResourceLocations" -> {CloudObject[
        "https://www.wolframcloud.com/obj/sw-writings/Resources/62b/\
62b4a705-7dbc-4429-b3df-69777ab309e2"]}, "Version" -> None, 
     "DefinitionNotebook" -> 
      CloudObject[
       "https://www.wolframcloud.com/obj/sw-writings/Medicine/\
CellularAutomatonHistoryPlot/CellularAutomatonHistoryPlot-\
DefinitionNotebook.nb"], 
     "DocumentationLink" -> 
      URL["https://www.wolframcloud.com/obj/sw-writings/Medicine/\
CellularAutomatonHistoryPlot"], "ExampleNotebookData" -> Automatic, 
     "FunctionLocation" -> 
      CloudObject[
       "https://www.wolframcloud.com/obj/sw-writings/Resources/62b/\
62b4a705-7dbc-4429-b3df-69777ab309e2/download/DefinitionData"], 
     "ShortName" -> "CellularAutomatonHistoryPlot", 
     "SymbolName" -> 
      "FunctionRepository`$62b4a7057dbc4429b3df69777ab309e2`\
CellularAutomatonHistoryPlot"|>]];
ggg = ResourceFunction[
     ResourceObject[<|"Name" -> "Data", 
       "UUID" -> "f89cae16-5ad6-4662-8ac2-4ad277c6b2e1", 
       "ResourceType" -> "Function", 
       "ResourceLocations" -> {CloudObject[
          "https://www.wolframcloud.com/obj/sw-writings/Resources/f89/\
f89cae16-5ad6-4662-8ac2-4ad277c6b2e1"]}, "Version" -> None, 
       "DefinitionNotebook" -> 
        CloudObject[
         "https://www.wolframcloud.com/obj/sw-writings/Medicine/Data/\
Data-DefinitionNotebook.nb"], 
       "DocumentationLink" -> 
        URL["https://www.wolframcloud.com/obj/sw-writings/Medicine/\
Data"], "ExampleNotebookData" -> Automatic, 
       "FunctionLocation" -> 
        CloudObject[
         "https://www.wolframcloud.com/obj/sw-writings/Resources/f89/\
f89cae16-5ad6-4662-8ac2-4ad277c6b2e1/download/DefinitionData"], 
       "ShortName" -> "Data", 
       "SymbolName" -> 
        "FunctionRepository`$f89cae165ad646628ac24ad277c6b2e1`Data", 
       "PageHeaderClickToCopy" -> 
        "ResourceObject[CloudObject[\"https://www.wolframcloud.com/\
obj/sw-writings/Medicine/Data\"]]"|>]]["$LifeData"][
   "Gosper glider gun"];
Manipulate[
 simulation["GameOfLife", {ggg["MatrixData"], 0}, generations, 
  ImageSize -> 500, 
  PlotLabel -> 
   Style[Row[{"Generation ", generations}], 16, Bold]], {{generations,
    0, "Generations"}, 0, 100, 1, Appearance -> "Labeled"}, 
 Button["Reset", generations = 0], TrackedSymbols :> {generations}, 
 Paneled -> False, FrameMargins -> 0, ControlPlacement -> Bottom]

Forward Back

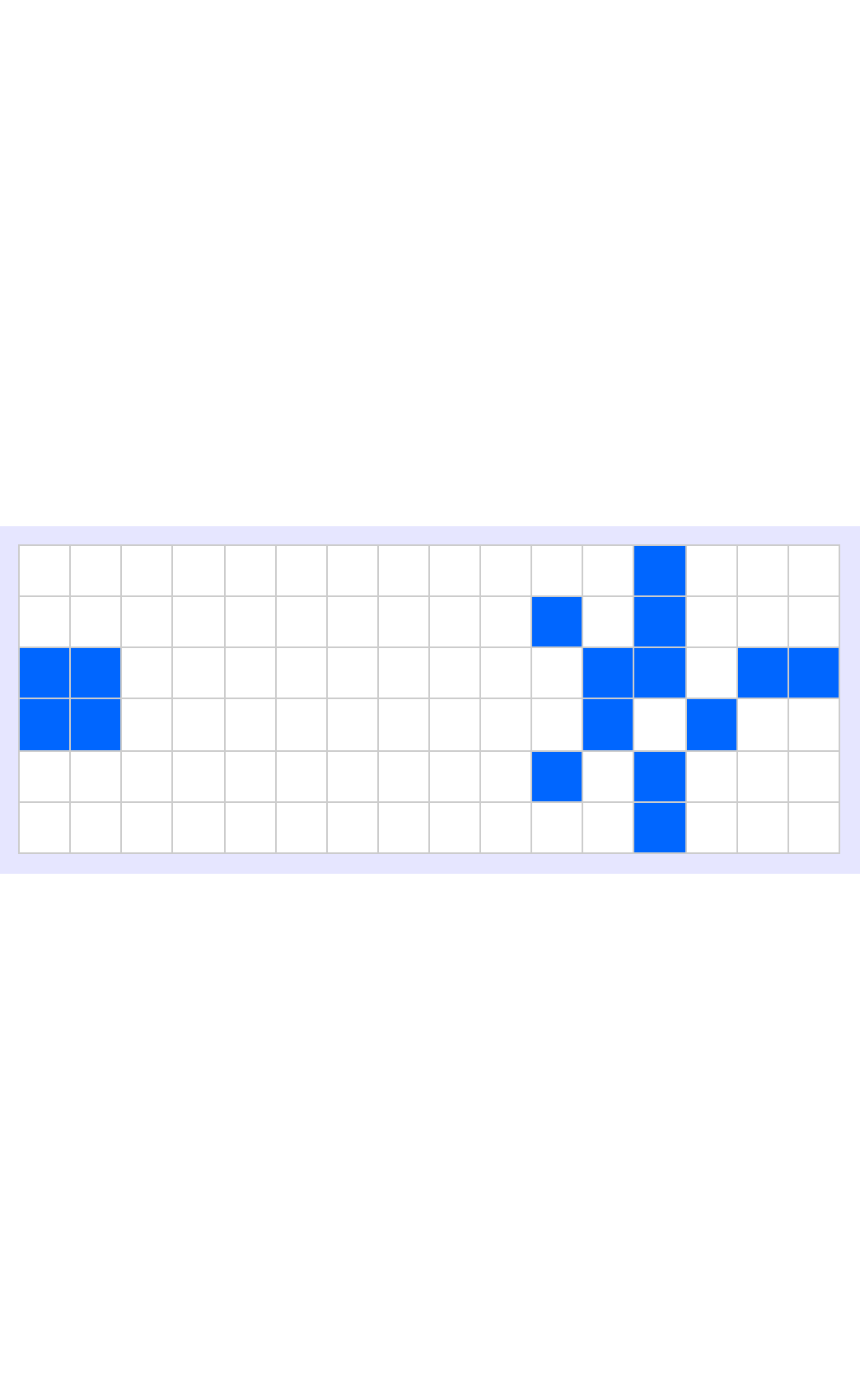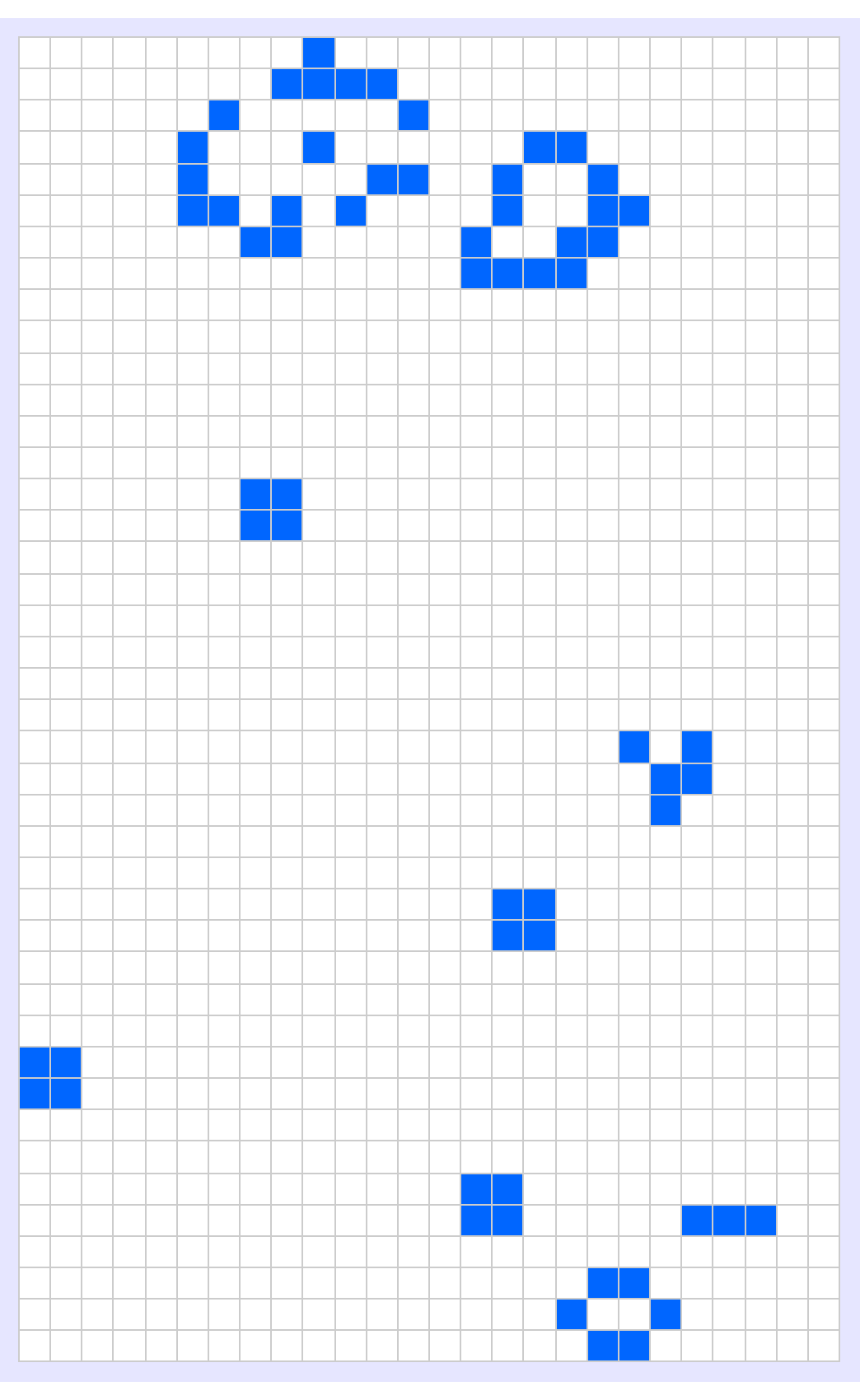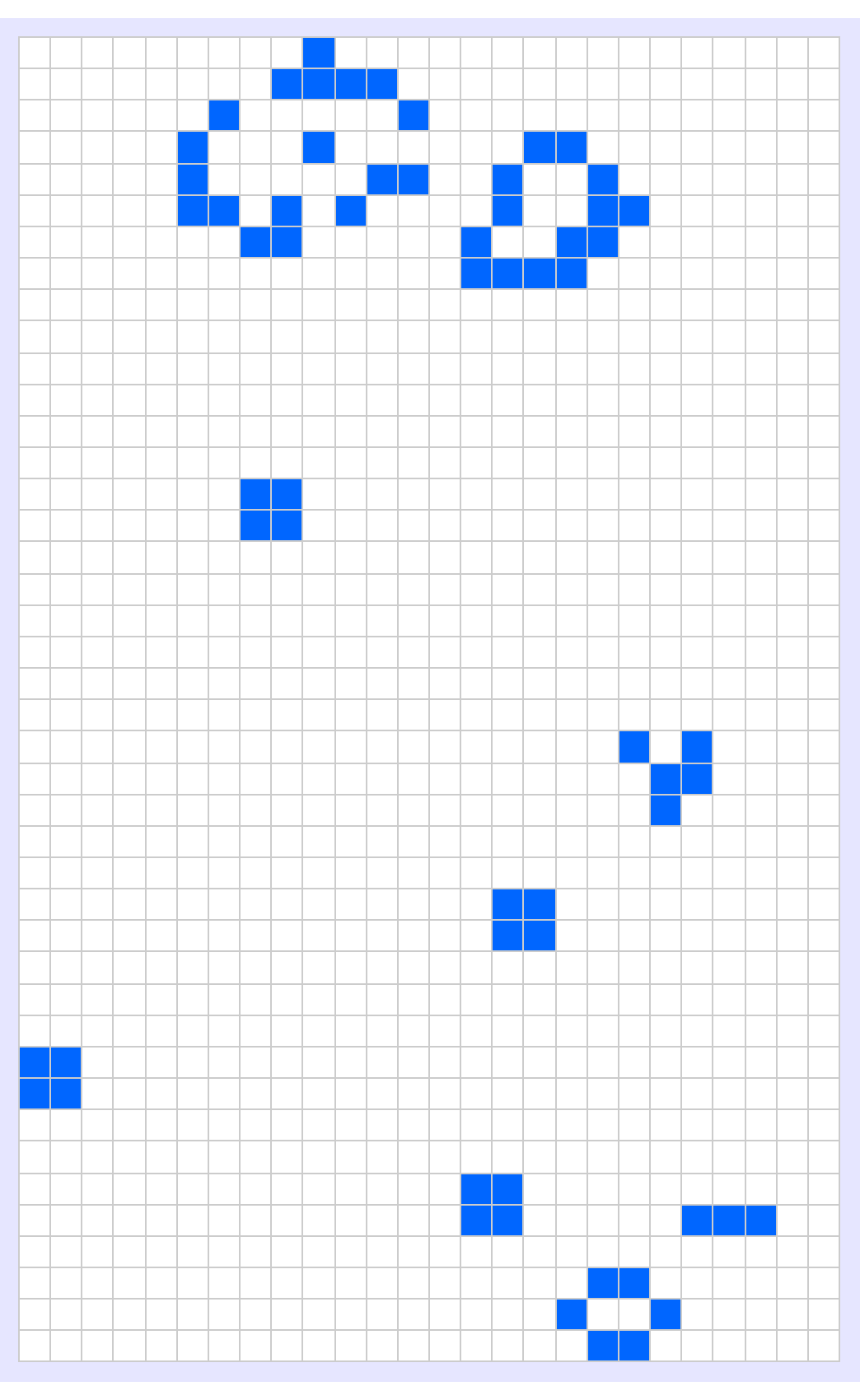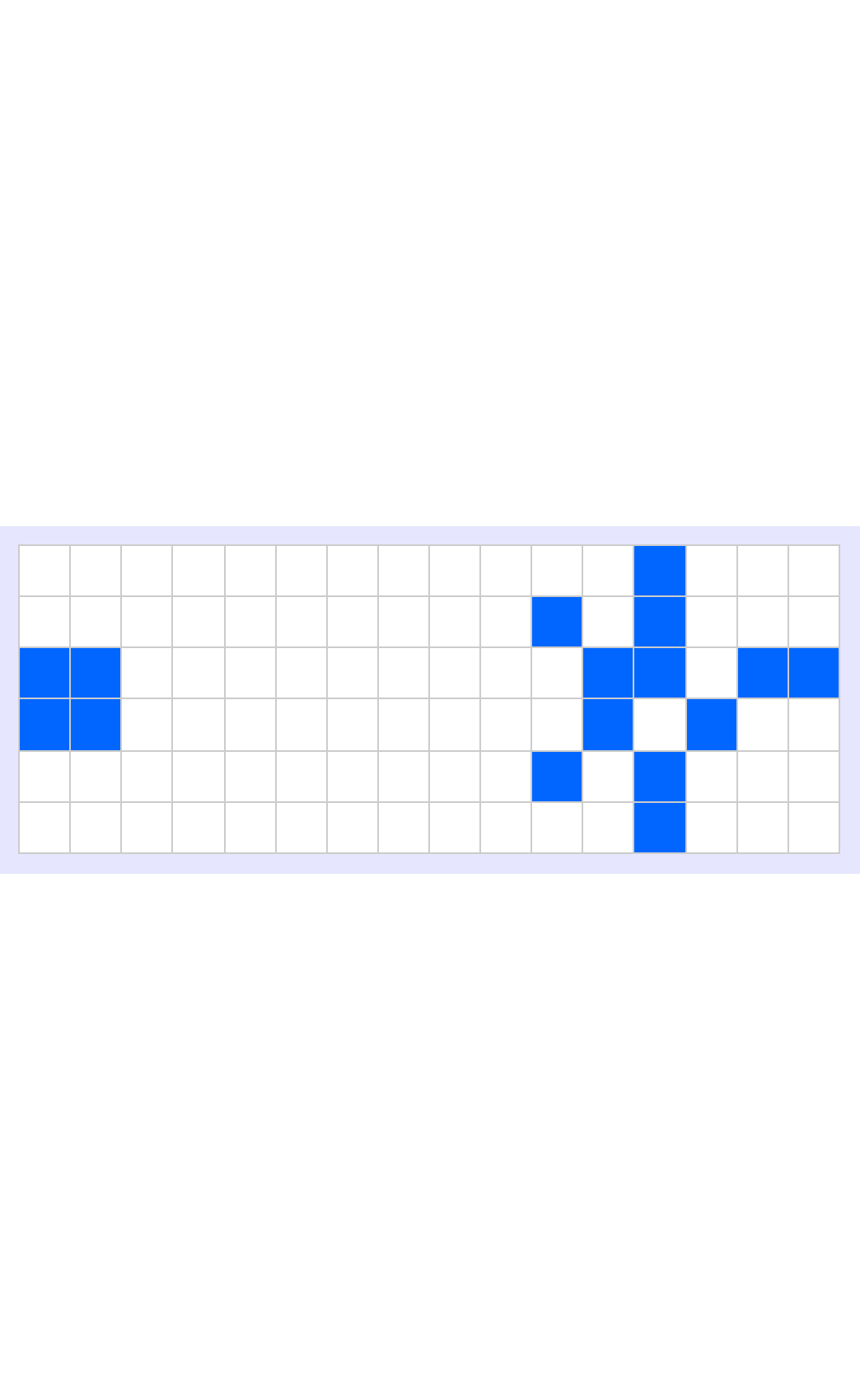
The beauty of Conway's Game of Life is shaping up to be evident through the modern computational tools that make these striking graphical representations possible, in no small part due to the structured grids of Mathematica which make patterns discovered and discoverable; the periodic & stable behaviors inherent in these patterns are rendered observable, evolving patterns like the famous Gosper Glider Gun, an endlessly winding and repeating configuration that generates gliders, continuously! 

gosperGun = {{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
     0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
    0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
    0, 1, 1}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 
    0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1}, {1, 1, 0, 
    0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 
    1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 
    0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 
    0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 
    0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 
    0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
    0, 0, 0, 0, 0}};
steps = 150;
currentState = gosperGun;
ages = ConstantArray[0, Dimensions[currentState]];
framesGosper = 
  Table[nextState = 
    CellularAutomaton["GameOfLife", currentState, 1][[2]];
   {currentRows, currentCols} = Dimensions[ages];
   {nextRows, nextCols} = Dimensions[nextState];
   paddedAges = PadRight[ages, {nextRows, nextCols}, 0];
   newAges = 
    MapThread[If[#2 == 1, #1 + 1, 0] &, {paddedAges, nextState}, 2];
   frameGosper = 
    ArrayPlot[newAges, ColorFunction -> "Rainbow", 
     ColorFunctionScaling -> False, PlotRange -> {0, 20}, 
     Mesh -> True, MeshStyle -> Directive[Opacity[0.15], Gray], 
     Frame -> False, ImageSize -> 800, 
     Epilog -> 
      Inset[Style["Step " <> ToString[i], Bold, 18, White], 
       Scaled[{0.1, 0.9}]]];
   currentState = nextState;
   ages = newAges;
   frameGosper, {i, 1, steps}];
Export["GosperGun_Evolution.mp4", framesGosper, 
  "VideoEncoding" -> "H264"];

Gosper Gun Game of Evolution GIF

Conway's Game of Life particularly shines through these interactive explorations that, illustrate the periodic inundation of gliders' firing from the gun, which just go to show the continuous and self-sustaining activity of certain Game of Life configurations; experiments starting from random initial states reveal how we can try unexpected structures and spontaneous and lively evolution of generational interaction that serves as the foundation of something that isn't required but is what we can clearly depict in our 3D spacetime plot: the evolution of patterns temporally over time, which allows viewers to observe and understand how seemingly chaotic and randomized beginnings can lead to stable or cyclic patterns. 

initRandom = RandomInteger[{0, 1}, {50, 50}];
steps = 200;
ageGrid = ConstantArray[0, Dimensions[initRandom]];
framesRandom = 
  Table[current = 
    CellularAutomaton["GameOfLife", initRandom, {{i}}][[1]];
   ageGrid = 
    MapThread[If[#2 == 1, #1 + 1, 0] &, {ageGrid, current}, 2];
   frameRandom = 
    ArrayPlot[ageGrid, 
     ColorFunction -> (Blend[{Transparent, Darker[Green], 
          Lighter[Green, 0.5], Yellow}, #] &), 
     ColorFunctionScaling -> False, Frame -> False, 
     PlotRange -> {0, 20}, PlotRangePadding -> 0, ImageSize -> 800, 
     Epilog -> 
      Inset[Style["Step " <> ToString[i], Bold, 18, Black], 
       Scaled[{0.1, 0.9}]]];
   frameRandom, {i, 0, steps}];
Export["LifeEvolution_Different.mp4", framesRandom, 
  "FrameRate" -> 30];

Life Evolution Different

The semantic connections to Natural Language Processing "NLP", of Conway's Game of Life patterns naturally extend discussions presented in previous analyses, such as the visualization of semantic embeddings in NLP using t-SNE. t-SNE dimensionality reduction techniques do provide visual clusters of semantically related words, and if the analogy goes that far the Game of Life provides clusters and evolutionary insights into cell behaviors. That's why I find myself revealing comparative Game of Life visualizations that underlie mathematical symmetries in the Ruliad of all human understanding. I think that the semantic embeddings in NLP can best be explained by the connection between our geometric intuition and the structures of mathematics such as those, we visualize in π's digit expansions and Conway's Game of Life. Just as embeddings in NLP map words into continuous vector spaces, bringing about subtle semantic relationships, our representations of π map digits into spiral structures, illuminating hidden numeric relationships. 

pulsar = {{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 1, 1, 1, 
    0, 0, 0, 1, 1, 1, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0,
     1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0}, {0, 1, 0, 0, 0, 0, 1, 0, 0, 
    0, 0, 1, 0}, {0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0}, {0, 0, 0, 1,
     1, 1, 0, 0, 0, 1, 1, 1, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
    0}, {0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0}, {0, 1, 0, 0, 0, 0, 1,
     0, 0, 0, 0, 1, 0}, {0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0}, {0, 
    1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 
    0, 0, 0, 0}};
pentadecathlon = {{0, 1, 1, 1, 1, 1, 1, 1, 1, 0}};
rPentomino = {{0, 1, 1}, {1, 1, 0}, {0, 1, 0}};
gosperGun = {{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
     0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
    0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
    0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 
    0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 1, 0, 
    0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 
    1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 
    0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 
    0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 
    0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 
    0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
    0, 0, 0, 0, 0}};
lwss = {{0, 1, 0, 0, 1}, {1, 0, 0, 0, 0}, {1, 0, 0, 0, 1}, {1, 1, 1, 
    1, 0}};
acorn = {{0, 1, 0, 0, 0, 0, 0}, {0, 0, 0, 1, 0, 0, 0}, {1, 1, 0, 0, 1,
     1, 1}};
simulateData[pattern_, gens_, offset_, fixedColor_] := 
 Module[{sim, data, centerX = 26, centerY = 26}, 
  sim = CellularAutomaton[
    "GameOfLife", {pattern, 0}, {gens, {-25, 25}, {-25, 25}}];
  data = 
   Flatten[Table[
     If[sim[[t, i, j]] == 1, {j - centerX + offset[[1]], 
       i - centerY + offset[[2]], t - 1, fixedColor}, Nothing], {t, 1,
       Length[sim]}, {i, 1, Dimensions[sim[[1]]][[1]]}, {j, 1, 
      Dimensions[sim[[1]]][[2]]}], 2];
  data]
patterns = {{"Pulsar", pulsar, {-40, 20}, Red}, {"Pentadecathlon", 
    pentadecathlon, {-40, -20}, Orange}, {"R-pentomino", 
    rPentomino, {0, 20}, Yellow}, {"Gosper Gun", gosperGun, {0, -20}, 
    Green}, {"Lightweight Spaceship", lwss, {40, 20}, Blue}, {"Acorn",
     acorn, {40, -20}, Magenta}};
allData = 
  Flatten[Map[Function[p, simulateData[p[[2]], 50, p[[3]], p[[4]]]], 
    patterns], 1];
legend = 
  SwatchLegend[{Red, Orange, Yellow, Green, Blue, Magenta}, {"Pulsar",
     "Pentadecathlon", "R-pentomino", "Gosper Gun", 
    "Lightweight Spaceship", "Acorn"}, LegendMarkerSize -> 20, 
   LabelStyle -> {Black, 16}];
Legended[
 Graphics3D[{Opacity[0.9], Specularity[White, 20], 
   Map[{#[[4]], Sphere[#[[1 ;; 3]], 0.3]} &, allData]}, Axes -> True, 
  AxesStyle -> Directive[White, Thick], 
  AxesLabel -> {Style["X", 18, Bold, White], 
    Style["Y", 18, Bold, White], 
    Style["Generation", 18, Bold, White]}, 
  PlotRange -> {{-70, 70}, {-40, 40}, {0, 50}}, Boxed -> False, 
  Lighting -> {{"Ambient", GrayLevel[0.3]}, {"Directional", 
     White, {2, -3, 1}}}, ViewPoint -> {3, -2, 1}, 
  ViewVertical -> {0, 0, 1}, ImageSize -> 800], legend]

All Pulsars N

The conceptual idea of recurrence in semantic embedding spaces is that recurrence plots, which are ordinarily and often used to identify periodic structures or hidden correlations in seemingly random sequences, correspond directly to the manner in which semantic embeddings cluster related concepts, forming visually identifiable "islands" of meaning within an otherwise abstract space. Our logarithmic spiral structures, which arrange π's digits exponentially outward, metaphorically align with a change in mindset in how NLP embeddings often distribute words exponentially in multidimensional spaces based on semantic similarity. This analogy helps conceptualize the mathematical foundation underpinning NLP techniques such as Word2Vec or ConceptNet Numberbatch. Further, I think that the interactivity of the Shadertoys which form the basis of our real-time rendering capabilities provide a temporal dimension. They offer not only static snapshots but also evolving representations--much like how NLP semantic embeddings adapt and evolve based on linguistic context. 

maxSteps = 200;
xRange = {-25, 35};
yRange = {-45, 45};
initialState = {{{0, 1, 1}, {1, 1, 0}, {0, 1, 0}}, 0};
evolution = 
  Table[CellularAutomaton["GameOfLife", 
    initialState, {{{i}}, xRange, yRange}], {i, 0, maxSteps}];
gridSize = Dimensions[evolution[[1]]];
ageEvolution = ConstantArray[0, gridSize];
ageFrames = {ageEvolution};
Do[currentState = evolution[[i]];
  ageEvolution = 
   MapThread[If[#2 == 1, #1 + 1, 0] &, {ageEvolution, currentState}, 
    2];
  AppendTo[ageFrames, ageEvolution], {i, 2, maxSteps + 1}];
ageColor[age_] := 
  If[age == 0, Gray, Blend["Rainbow", (age - 1)/(maxSteps - 1)]];
legend = 
  BarLegend[{"Rainbow", {1, maxSteps}}, LabelStyle -> {Bold, 14}, 
   LegendLabel -> Style["Cell Age", Bold, 16]];
frames = 
  Table[Legended[
    ArrayPlot[ageFrames[[i]], ColorFunction -> (ageColor[#] &), 
     ColorFunctionScaling -> False, Mesh -> True, 
     MeshStyle -> Directive[White, Opacity[0.15]], 
     PlotRange -> {0, maxSteps}, PlotRangePadding -> 0, Frame -> True,
      FrameLabel -> {Style["X", Bold, 16], Style["Y", Bold, 16]}, 
     PlotLabel -> Style["Generation " <> ToString[i - 1], Bold, 24], 
     ImageSize -> 800], legend], {i, 1, Length[ageFrames]}];
Export["LifeWithAge.mp4", frames, "FrameRate" -> 30]

LifeWithAge

Thus we can construct, the evolution of a Gosper Glider Gun. The Game of Life pattern periodically produces "gliders" (moving structures), via the sinusoidal viewpoint that makes the delineation of cell boundaries more apparent and thus the assembly of these patterns--the pulsar being an oscillator with a period of 3, the pentadecathlon oscillator with period 15, the R-Pentomino's chaotic growth and the Gosper Gun which repeatedly emits gliders, we can "combine" these in a rather non-interactive way such that the Lightweight Spaceship travels across the grid while the Acorn grows unpredictably into complex patterns. This offset forms patterns organizationally tracking the ages of cells, which indicate cell longevity through the classic rainbow color scheme. 

spacetimeFrames = 
  Table[ListPlot3D[
    CellularAutomaton[
     "GameOfLife", {{{1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
        0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
        0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
        0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 
        0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0,
         0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1}, {0, 0, 0, 0, 0, 0, 0, 0,
         0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 
        0, 0, 0, 0, 0, 0, 1, 1}, {1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 
        0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
         0, 0, 0}, {1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1,
         1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0,
         0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 
        0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 
        0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
         0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
         0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
        0, 0, 0, 0, 0, 0}}, 0}, {{{t}}, {-20, 40}, {-20, 40}}], 
    Mesh -> True, MeshStyle -> Opacity[0.2], 
    ColorFunction -> "Rainbow", Boxed -> False, Axes -> False, 
    PlotRangePadding -> 0, ViewPoint -> {3 Sin[t/10], 3 Cos[t/10], 1},
     ImageSize -> 500], {t, 0, 50}];
Export["GliderGun3D.mp4", spacetimeFrames]

GliderGun3D

Inter-actions over 200 generations, specifically focus not just on the iconic diagonal motion and repetitive nature of gliders but also on the aesthetic appeal, which builds upon the enduring appeal of Conway's Game of Life in all its simple rules and, astonishingly complex emergent behaviors. I think the statistical summary of pattern discoveries impressively spanning decades as well as the evolution of the automata as rotating three-dimensional structures, really bring us back to the interactions in obscurity as they occur in traditional, two-dimensional representations. Simultaneously Mathematica evolves multiple classic patterns--such as pulsars, pentadecathlons, R-pentominos, Gosper guns, lightweight spaceships (LWSS), and acorns--both strategically on a single expansive grid with tracking of the presence of cells..as well as the presentation of their ages using color gradients, which distinguishes the pattern-based interaction--merge, stabilize, or dissipate over time. These resulting animations effectively communicate how we can create a new interaction that is based on complex initial conditions. 

gridDims = {61, 91};  
toIndex[{r_, c_}] := {r + 26, c + 46};
pulsar = {{2, 0}, {3, 0}, {4, 0}, {8, 0}, {9, 0}, {10, 0}, {0, 2}, {5,
     2}, {7, 2}, {12, 2}, {0, 3}, {5, 3}, {7, 3}, {12, 3}, {0, 4}, {5,
     4}, {7, 4}, {12, 4}, {2, 5}, {3, 5}, {4, 5}, {8, 5}, {9, 5}, {10,
     5}, {2, 7}, {3, 7}, {4, 7}, {8, 7}, {9, 7}, {10, 7}, {0, 8}, {5, 
    8}, {7, 8}, {12, 8}, {0, 9}, {5, 9}, {7, 9}, {12, 9}, {0, 10}, {5,
     10}, {7, 10}, {12, 10}, {2, 12}, {3, 12}, {4, 12}, {8, 12}, {9, 
    12}, {10, 12}};
pentadecathlon = {{1, 0}, {2, 0}, {0, 1}, {3, 1}, {0, 2}, {3, 2}, {0, 
    3}, {3, 3}, {1, 4}, {2, 4}};
rPentomino = {{1, 0}, {2, 0}, {0, 1}, {1, 1}, {1, 2}};
gosperGun = {{0, 4}, {0, 5}, {1, 4}, {1, 5}, {10, 4}, {10, 5}, {10, 
    6}, {11, 3}, {11, 7}, {12, 2}, {12, 8}, {13, 2}, {13, 8}, {14, 
    5}, {15, 3}, {15, 7}, {16, 4}, {16, 5}, {16, 6}, {17, 5}, {20, 
    2}, {20, 3}, {20, 4}, {21, 2}, {21, 3}, {21, 4}, {22, 1}, {22, 
    5}, {24, 0}, {24, 1}, {24, 5}, {24, 6}, {34, 2}, {34, 3}, {35, 
    2}, {35, 3}};
lwss = {{1, 0}, {2, 0}, {3, 0}, {4, 0}, {0, 1}, {4, 1}, {4, 2}, {0, 
    3}, {3, 3}};
acorn = {{1, 0}, {3, 1}, {0, 2}, {1, 2}, {4, 2}, {5, 2}, {6, 2}};
offsetPulsar = {-20, -30};
offsetPentadecathlon = {0, -40};
offsetRPentomino = {10, 0};
offsetGosper = {-10, 10};
offsetLWSS = {20, 20};
offsetAcorn = {-5, -10};
offsetPattern[pattern_, offset_] := Map[# + offset &, pattern];
compositeCoords = 
  Join[offsetPattern[pulsar, offsetPulsar], 
   offsetPattern[pentadecathlon, offsetPentadecathlon], 
   offsetPattern[rPentomino, offsetRPentomino], 
   offsetPattern[gosperGun, offsetGosper], 
   offsetPattern[lwss, offsetLWSS], offsetPattern[acorn, offsetAcorn]];
liveCellIndices = toIndex /@ compositeCoords;
initialGrid = SparseArray[liveCellIndices -> 1, gridDims];
initialState = {initialGrid, 0};
steps = 200;
ca = Table[
   CellularAutomaton["GameOfLife", 
    initialState, {{{i}}, {-25, 35}, {-45, 45}}], {i, 0, steps}];
ages = ConstantArray[0, Dimensions[ca[[1]]]];
ageHistory = 
  FoldList[MapThread[If[#2 == 1, #1 + 1, 0] &, {##}, 2] &, ages, ca];
ageHistory = ageHistory[[2 ;;]];
maxAge = Max[Flatten[ageHistory]];
frames = 
  ArrayPlot[#, 
     ColorFunction -> (Blend[{Black, ColorData["Rainbow"][#]}, 
         0.8] &), ColorFunctionScaling -> True, Frame -> False, 
     Mesh -> None, ImageSize -> 800, PlotRange -> {0, maxAge}, 
     Background -> None] & /@ ageHistory;
Export["ColorfulLifeEvolution.mp4", frames];

Colorful Life Evolution

For me, I think it's quite a powerful analytical technique to track and display the cell "age" using heatmap color gradients. Starting from random initial conditions at controlled densities, the cellular automaton evolves, and each cell accumulates age based on continuous activity. Mathematica's FoldList functionality elegantly manages these calculations with a need for speed, offering a nuanced view of the automaton's stability and longevity of particular patterns. It is the heatmap that complements otherwise hidden structures, such as persistent oscillators or traveling waves that sustain activity over extensive periods. 

size = 100; 
steps = 200; 
density = 0.2; 
initialGrid = 
  RandomInteger[BernoulliDistribution[density], {size, size}];
sim = CellularAutomaton["GameOfLife", initialGrid, steps];
ageEvolution = 
  FoldList[MapThread[If[#2 == 1, #1 + 1, 0] &, {#1, #2}, 2] &, 
   sim[[1]], Rest[sim]];
maxAge = Max[Flatten[ageEvolution]];
frames = 
  Table[ArrayPlot[ageEvolution[[i]], 
    ColorFunction -> (If[# == 0, Transparent, 
        Blend["Rainbow", #/maxAge]] &), ColorFunctionScaling -> False,
     Frame -> False, PlotRangePadding -> 0, ImageSize -> 500], {i, 1, 
    Length[ageEvolution]}];
Export["LifeAgeHeatmap.mp4", frames, "VideoEncoding" -> "H264"];

LifeAgeHeatmap

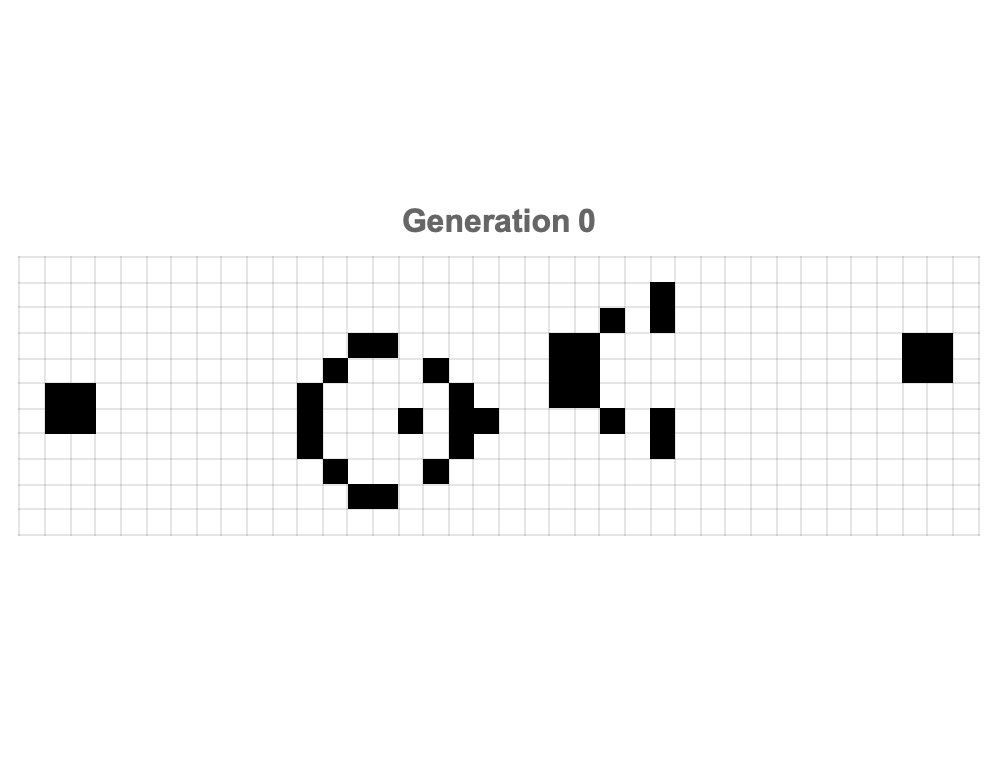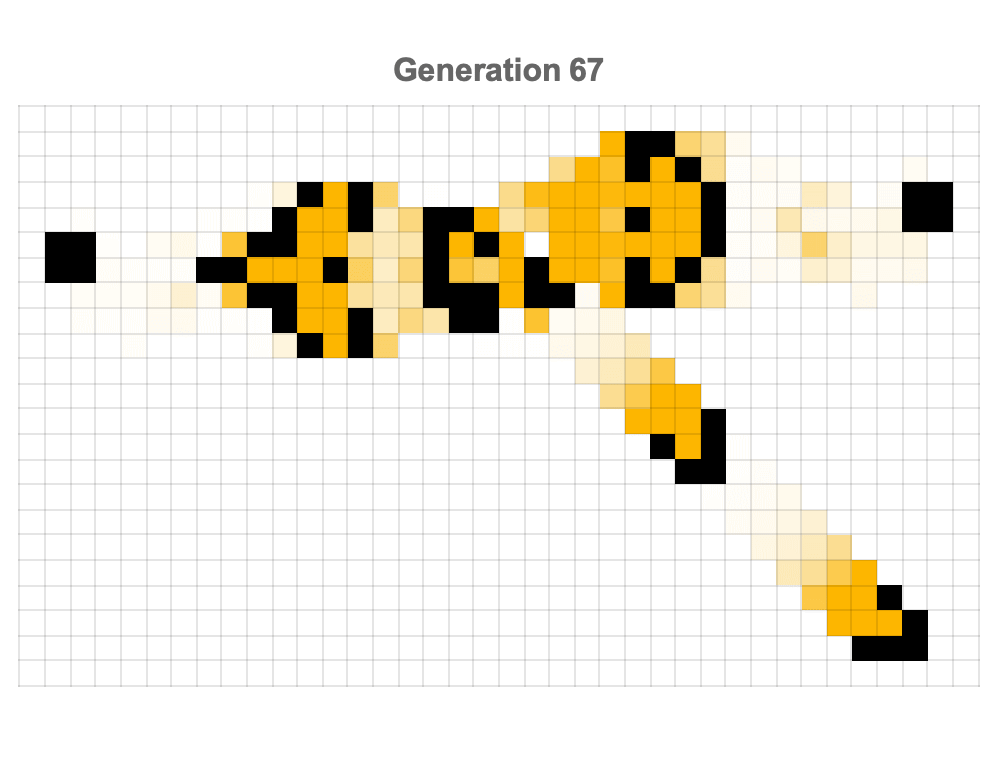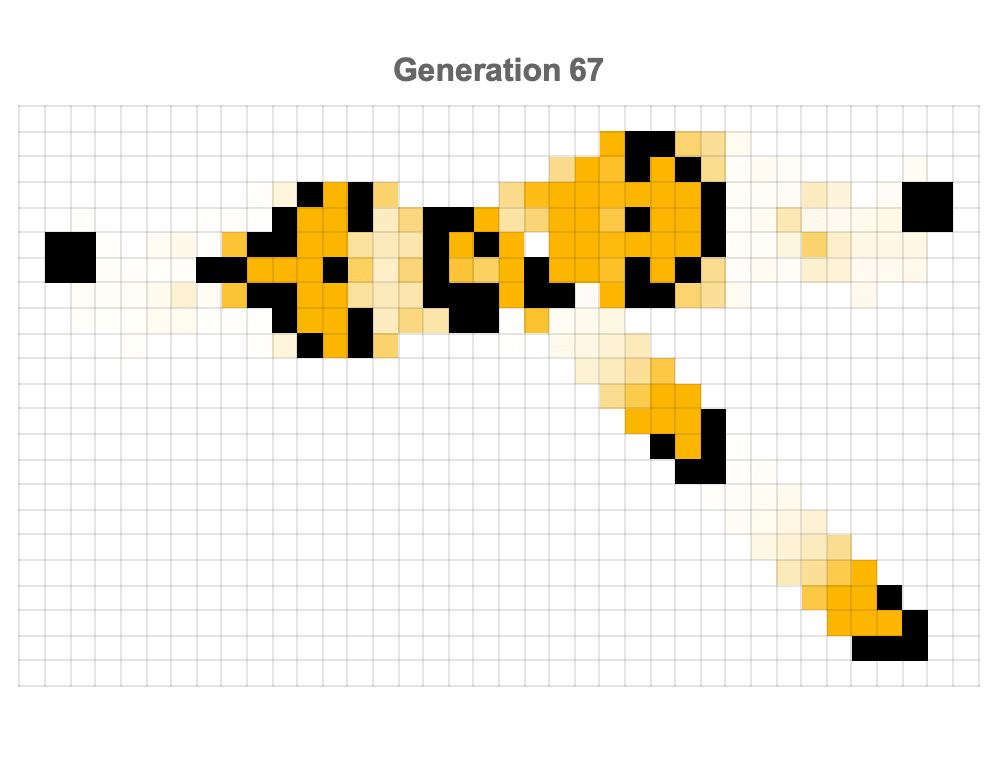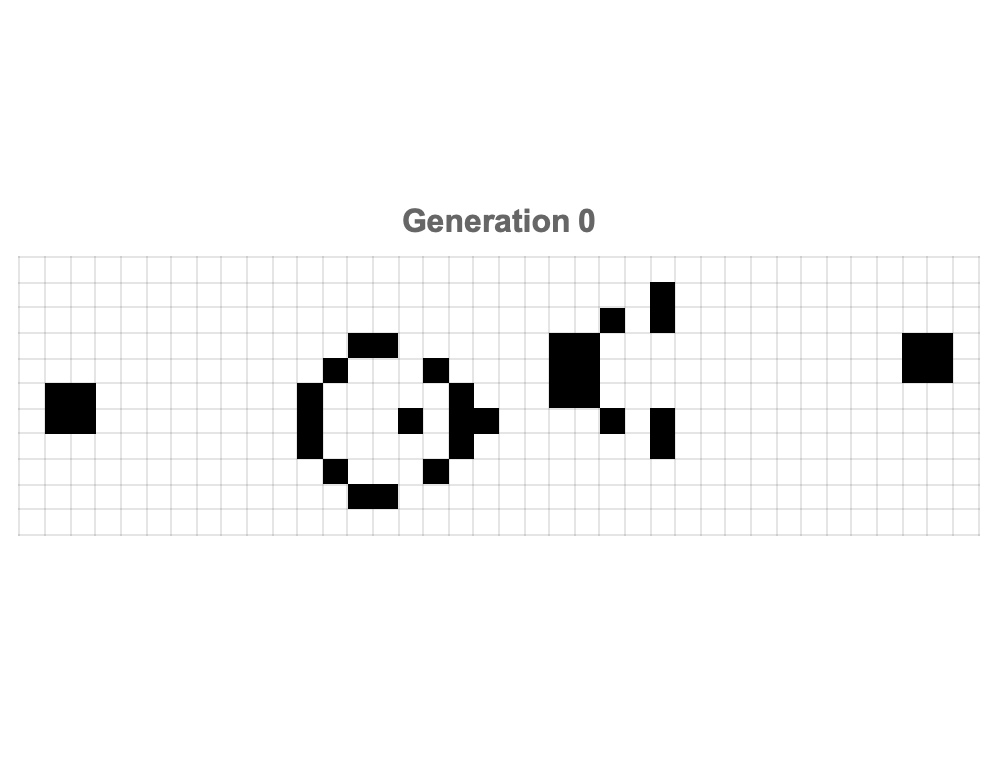
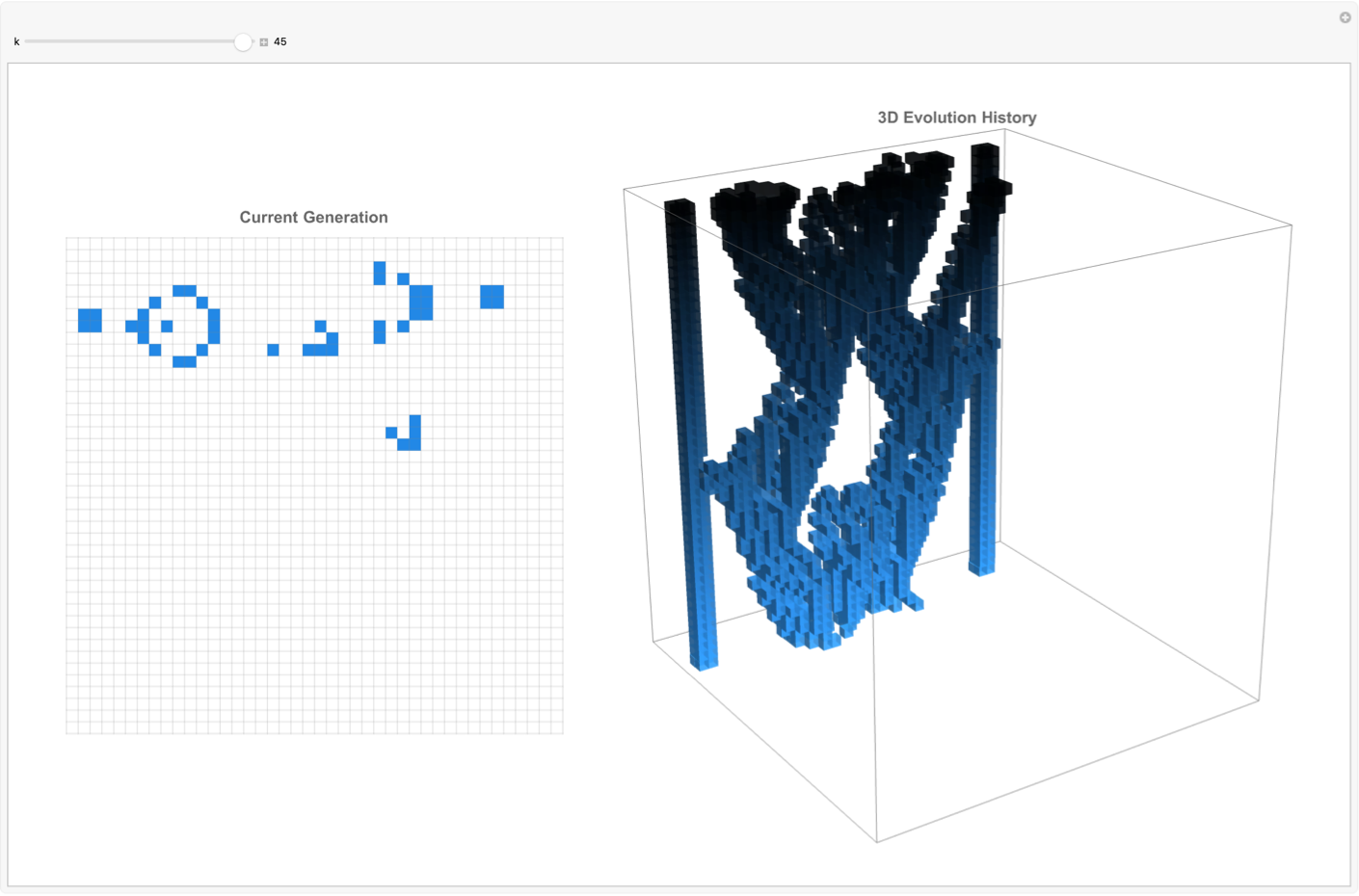
Mathematica, excels at creating interactive environments using Manipulate, providing researchers and educators alike the means to watch the Game of Life interactively. Users can observe current generations side by side with historical three-dimensional representations of their evolution, gaining admirable status in initial configurations and how they influence future states. Tools such as stepwise animators with playback controls enable detailed, and I'm sure user-driven exploration, fostering a hands-on approach to understanding artificial phenomena. 

Manipulate[
 Module[{currentState, historyPlot}, currentState = evolution[[k + 1]];
  historyPlot = Take[evolution, k + 1];
  GraphicsRow[{ArrayPlot[currentState, Mesh -> True, 
     MeshStyle -> Directive[Opacity[0.2], Gray], 
     ColorRules -> {1 -> Hue[0.58, 0.85, 0.9], 0 -> White}, 
     PlotLabel -> Style["Current Generation", Bold, 14], 
     ImageSize -> 300], 
    Graphics3D[{EdgeForm[None], 
      Table[If[
        historyPlot[[t + 1, i, j]] == 1, {Opacity[0.7], 
         Hue[0.58, 0.8, 1 - t/(k + 1)], 
         Cuboid[{i, j, t}, {i + 1, j + 1, t + 1}]}, Nothing], {t, 0, 
        k}, {i, 1, rows}, {j, 1, cols}]}, Boxed -> True, 
     Lighting -> "Neutral", ViewPoint -> {3, -2, 1.5}, 
     ImageSize -> 400, 
     PlotRange -> {{1, rows + 1}, {1, cols + 1}, {0, maxSteps + 1}}, 
     PlotLabel -> Style["3D Evolution History", Bold, 14]]}, 
   ImageSize -> Full]], {k, 0, 45, 1, Appearance -> "Labeled"}, 
 Initialization :> (gosper = 
    SparseArray[{{6, 1} -> 1, {7, 1} -> 1, {6, 2} -> 1, {7, 2} -> 
       1, {6, 11} -> 1, {7, 11} -> 1, {8, 11} -> 1, {5, 12} -> 
       1, {9, 12} -> 1, {4, 13} -> 1, {10, 13} -> 1, {4, 14} -> 
       1, {10, 14} -> 1, {7, 15} -> 1, {5, 16} -> 1, {9, 16} -> 
       1, {6, 17} -> 1, {7, 17} -> 1, {8, 17} -> 1, {7, 18} -> 
       1, {4, 21} -> 1, {5, 21} -> 1, {6, 21} -> 1, {4, 22} -> 
       1, {5, 22} -> 1, {6, 22} -> 1, {3, 23} -> 1, {7, 23} -> 
       1, {3, 25} -> 1, {7, 25} -> 1, {2, 25} -> 1, {8, 25} -> 
       1, {4, 35} -> 1, {5, 35} -> 1, {4, 36} -> 1, {5, 36} -> 
       1}, {40, 40}];
   maxSteps = 45;
   evolution = CellularAutomaton["GameOfLife", gosper, maxSteps];
   {rows, cols} = Dimensions[gosper];
   evolution = ArrayPad[#, 1] & /@ evolution;
   {rows, cols} = Dimensions[evolution[[1]]];)]

3d evolution

Statistically and historically, Mathematica supports cellular automata discoveries by aggregating pattern discovery data over decades, that's how we got these informative histograms and box-and-whisker plots. These tools reveal trends we don't even have, such as periods of increased discovery or focused research activities around specific pattern types (oscillators, guns, puffers, etc.), customizing context and perspective on the evolution of Game of Life research as a scientific endeavor. 

initial = 
  SparseArray[Automatic, {31, 26}, 
   0, {1, {{0, 3, 6, 8, 8, 16, 23, 28, 31, 37, 45, 52, 57, 59, 65, 68,
       74, 79, 84, 88, 93, 94, 97, 101, 104, 109, 112, 113, 119, 124, 
      127, 129}, {{5}, {6}, {7}, {4}, {7}, {8}, {4}, {9}, {4}, {5}, \
{6}, {10}, {11}, {13}, {14}, {15}, {2}, {3}, {5}, {7}, {12}, {14}, \
{15}, {4}, {7}, {12}, {15}, {16}, {1}, {4}, {13}, {1}, {6}, {9}, \
{10}, {13}, {16}, {2}, {4}, {5}, {6}, {9}, {10}, {14}, {15}, {4}, \
{5}, {7}, {9}, {10}, {12}, {16}, {10}, {11}, {13}, {14}, {15}, {10}, \
{16}, {13}, {14}, {15}, {18}, {19}, {20}, {16}, {18}, {19}, {11}, \
{12}, {14}, {18}, {19}, {20}, {11}, {12}, {15}, {18}, {19}, {13}, \
{14}, {15}, {16}, {20}, {14}, {15}, {17}, {20}, {12}, {13}, {15}, \
{17}, {19}, {15}, {12}, {20}, {21}, {13}, {14}, {20}, {21}, {15}, \
{16}, {18}, {17}, {18}, {19}, {22}, {24}, {17}, {18}, {22}, {18}, \
{19}, {20}, {21}, {22}, {23}, {25}, {20}, {21}, {24}, {25}, {26}, \
{20}, {21}, {26}, {24}, {25}}}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
     1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
      1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
     1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
      1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
     1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
      1, 1, 1, 1, 1, 1, 1, 1, 1}}];
evolution = CellularAutomaton["GameOfLife", initial, 100];
Manipulate[
 ArrayPlot[ArrayPad[evolution[[step]], 2], Mesh -> True, 
  MeshStyle -> {Opacity[0.1], Gray}, 
  ColorRules -> {1 -> Darker@Green, 0 -> White}, 
  PlotLabel -> 
   Style["Game of Life - Step " <> ToString[step - 1], 16, Bold], 
  ImageSize -> 600], {{step, 1, "Generation"}, 1, Length[evolution], 
  1, Animator, AnimationRate -> 5, AnimationRunning -> False, 
  AppearanceElements -> {"PlayPauseButton", "StepLeftButton", 
    "StepRightButton", "FasterSlowerButtons", "DirectionButton"}}, 
 ControlPlacement -> Bottom, Paneled -> False, FrameMargins -> 0]

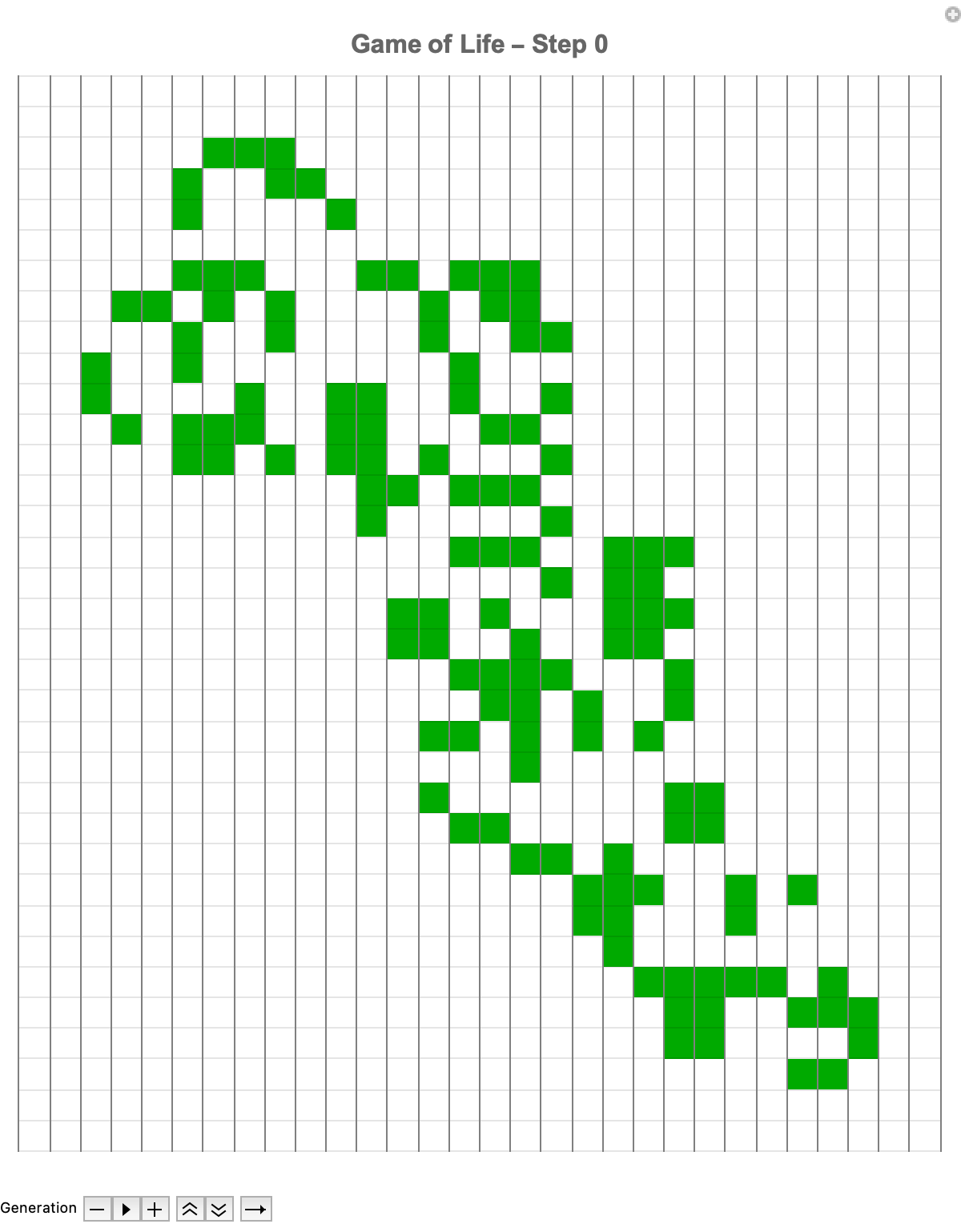
step 0 game of life

Like the Jacobian with the derivative stencil, it is the sparse representation that is invaluable for efficient simulation; sparse arrays show the initial states for Conway's Game of Life. Sparse arrays are quite efficient for simulations because they store only non-zero (or "alive") cells, greatly reducing computational "overhead". The sparse representation of the SparseArray specifies the initial positions of live cells within say a 31 by 26 grid. This careful initialization makes it possible for users to precisely define some patterns without too much processing time; as these patterns evolve we can pause, rewind, and fast-forward through generations of evolution. 

gliderPositions = {{1, 2}, {2, 3}, {3, 1}, {3, 2}, {3, 3}};
initial = SparseArray[gliderPositions -> 1, {30, 30}];
evolution = CellularAutomaton["GameOfLife", initial, 50];
data3D = 
  Flatten[Table[
    If[evolution[[t, i, j]] == 1, {i, j, t}, Nothing], {t, 
     Length[evolution]}, {i, Dimensions[evolution[[t]]][[1]]}, {j, 
     Dimensions[evolution[[t]]][[2]]}], 2];
Manipulate[
 GraphicsRow[{ArrayPlot[evolution[[t]], Mesh -> True, 
    MeshStyle -> Opacity[0.1], 
    PlotLabel -> "Step " <> ToString[t - 1], ImageSize -> Medium], 
   ListPointPlot3D[Select[data3D, #[[3]] <= t &], 
    ColorFunction -> Function[{x, y, z}, Hue[z/Length[evolution]]], 
    PlotRange -> {{1, 30}, {1, 30}, {1, Length[evolution]}}, 
    AxesLabel -> {"X", "Y", "Time"}, BoxRatios -> {1, 1, 1}, 
    ImageSize -> Medium, 
    PlotLabel -> "3D Evolution up to Step " <> ToString[t - 1]]}, 
  Spacings -> 0], {{t, 1, "Generation"}, 1, Length[evolution], 1, 
  ControlType -> Animator, AnimationRate -> 5, 
  AnimationDirection -> "ForwardBackward"}, ControlPlacement -> Top, 
 TrackedSymbols :> {t}]

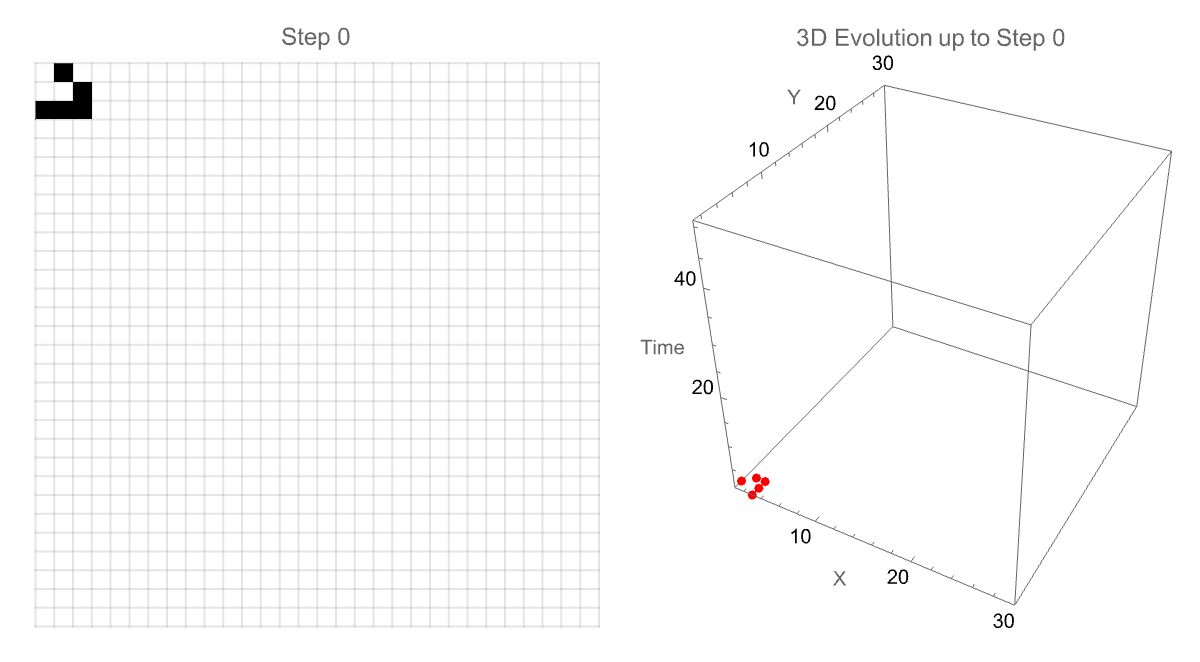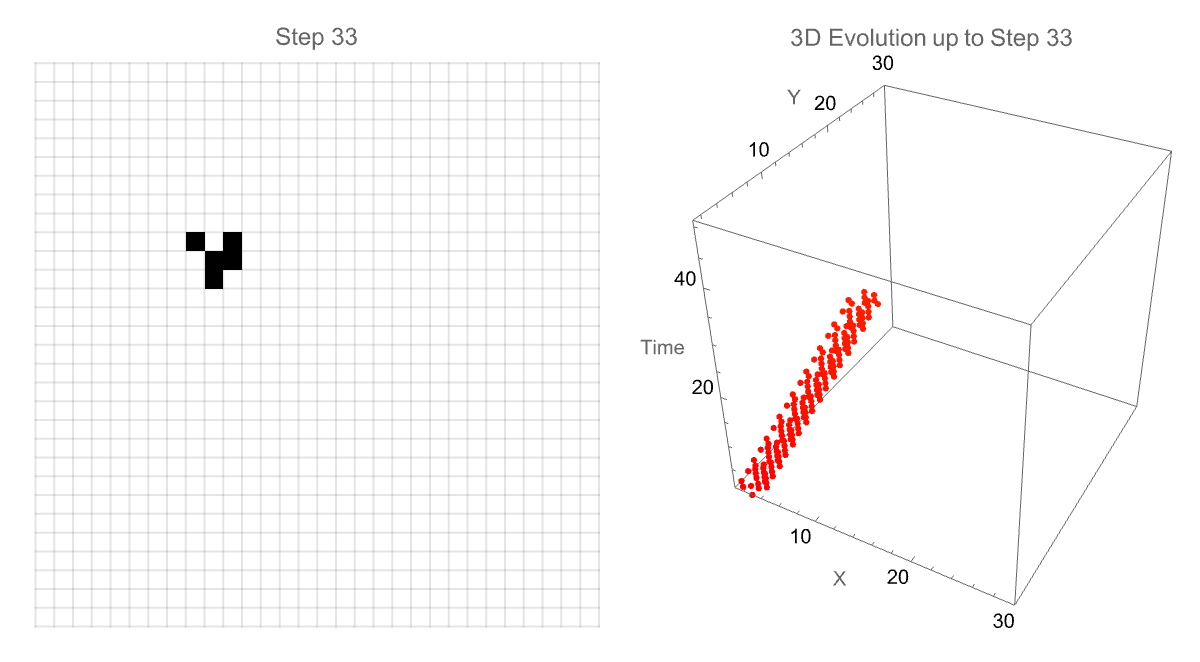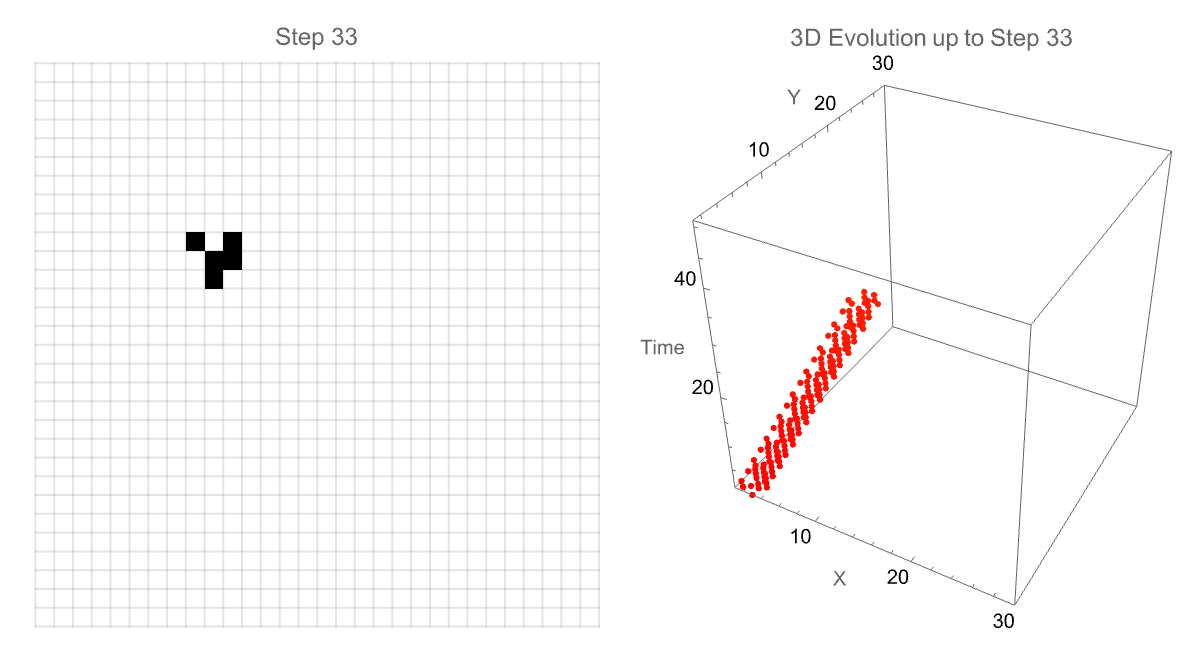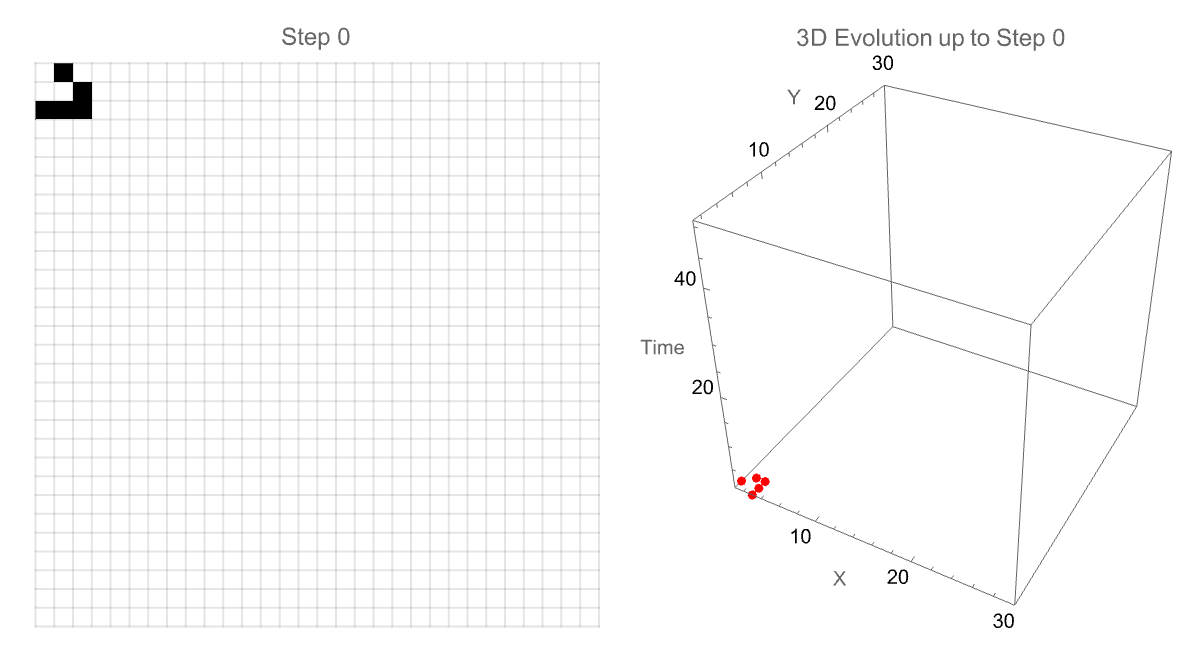
Interactive Glider

We can also alter the animation speed as well as explore the patterns in depth, observing how complex structures evolve or stabilize over time. I think the interactivity of these gliders, the 3-dimensional glider evolution is transformative from traditional two-dimensional data "onto" a 3-dimensional environment. The classic "glider" in motion is "done" in part within the simulation, tracking its path as it moves diagonally across the grid. And then the subsequent generation of the 3-dimensional model that shows precisely how the glider travels over generations is what adds the extra temporal dimension to its trajectory as portrayed--speed, periodicity, and directional..stability of specific patterns and pattern discoveries in the Game of Life are made clear, categorized into various structures. 

yearRange = {1969, 2025};
patternData = <|
   "Oscillator" -> 
    Uncompress[
     "1:eJztw1cKwjAYAOBffOg5vJJH8AD1bC60Ki5U1Lr33usYBsxDCH9IGi1SyQdfJB\
aP2iEAsMIACes9qTnl07TPMxqzZA7pSOaZBbKILDHL3Ipkla6RdWbji5vIlmRbYefHXc1d\
wd6H+woH9BA5IseSE+5UcMadkwvBJb3ycO3xRnCL3HH3yIPGo+\
IT86zxovjKvQXk3TQD8mGaf/6JfAGaYqdR"], 
   "Spaceship" -> 
    Uncompress[
     "1:eJylw10SgWAUgOHjyjrakiVYgMbSoi0YQsLE+Cuk0C68F9/FmTM1XXhmHm/\
oD0Y9ERkz6ItM1ClDzlrO1cUfI3PJFddm7G4aJuq24457puah5VE98cyLenVvbsacdz7Mp\
1uYL5YdK74bfvhlzR+FdGIt"], 
   "Gun" -> {1970, 1970, 1971, 1990, 1990, 1991, 1991, 1991, 1994, 
     1994, 1995, 1996, 1996, 1996, 1996, 1996, 1997, 1997, 1997, 1997,
      2000, 2003, 2003, 2003, 2004, 2009, 2009, 2009, 2010, 2013, 
     2013, 2013, 2015, 2016, 2017, 2017, 2018, 2018, 2018, 2018, 2020,
      2021, 2021, 2021, 2021, 2022, 2022, 2022, 2022, 2022, 2022, 
     2022, 2022, 2022, 2023, 2023, 2023, 2023, 2023, 2024, 2024, 2024,
      2024}, "Puffer" -> {1971, 1971, 1971, 1971, 1984, 1992, 1992, 
     1993, 1993, 2001, 2001, 2010, 2014, 2014, 2015, 2016, 2022, 
     2022}, "Conduit" -> {1972, 1995, 1996, 1996, 1996, 1996, 1996, 
     1996, 1996, 1996, 1996, 1996, 1996, 1996, 1996, 1996, 1997, 1997,
      1997, 1997, 1997, 1997, 1997, 1997, 1997, 1997, 1997, 1998, 
     1998, 1998, 1998, 1998, 2005, 2006, 2006, 2011, 2011, 2011, 2012,
      2013, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 
     2015, 2015, 2015, 2015, 2016, 2017, 2018, 2018, 2019, 2020, 2021,
      2022, 2022, 2022, 2022, 2022, 2023, 2024, 2024, 2024, 2024}, 
   "Reflector" -> {1993, 1994, 1998, 1998, 1998, 1998, 1998, 2001, 
     2002, 2009, 2009, 2012, 2013, 2013, 2016, 2016, 2016, 2016, 2016,
      2016, 2016, 2016, 2017, 2017, 2017, 2017, 2017, 2017, 2017, 
     2018, 2018, 2018, 2018, 2020, 2021, 2022, 2023, 2023}|>;
myPluralize[s_String] := s <> "s";
dashboardPanel = 
  Column[{GraphicsGrid[
     Partition[
      KeyValueMap[
       Histogram[#2, {1}, PlotRange -> {yearRange, Automatic}, 
         Frame -> True, FrameTicks -> {Automatic, None}, 
         ChartStyle -> 
          Directive[Opacity[0.8, ColorData[97][23]], 
           EdgeForm[Darker[ColorData[97][24]]]], 
         Epilog -> 
          Style[Text[myPluralize[#1], Scaled[{0.1, 0.85}], {-1, 0}], 
           11], AspectRatio -> 0.3, ImageSize -> 200] &, patternData],
       3], ImageSize -> 650, Spacings -> {3, 7}]
    }, Spacings -> 20, Alignment -> Center];
TabView[{"Dashboard" -> dashboardPanel}]

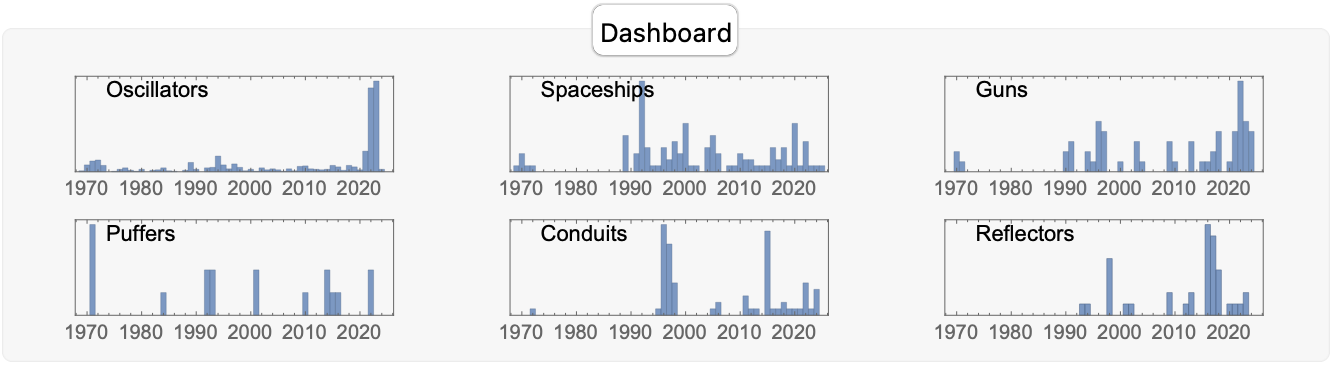
Dashboard

What are these structures? These structures are the Oscillators, Spaceships, Guns, Puffers, Conduits, and Reflectors introduced via a rather informative dashboard on, the historical context of these discoveries. That is how we know which pattern categories were explored or constructed most frequently over time; the trends, peaks, and gaps in exploration activity are easy to see when we prominently place certain patterns like guns and oscillators onto these histograms, during particular periods in cellular automata research. I think it is the pattern-discovery timelines that "neatly" provide statistically sound historical background into the years of active discovery or invention for each pattern type. 

data = <|"Oscillator" -> CompressedData["
1:eJztw1cKwjAYAOBffOg5vJJH8AD1bC60Ki5U1Lr33usYBsxDCH9IGi1SyQdf
JBaP2iEAsMIACes9qTnl07TPMxqzZA7pSOaZBbKILDHL3Ipkla6RdWbji5vI
lmRbYefHXc1dwd6H+woH9BA5IseSE+5UcMadkwvBJb3ycO3xRnCL3HH3yIPG
o+IT86zxovjKvQXk3TQD8mGaf/6JfAGaYqdR
"], "Spaceship" -> CompressedData["
1:eJylw10SgWAUgOHjyjrakiVYgMbSoi0YQsLE+Cuk0C68F9/FmTM1XXhmHm/o
D0Y9ERkz6ItM1ClDzlrO1cUfI3PJFddm7G4aJuq24457puah5VE98cyLenVv
bsacdz7Mp1uYL5YdK74bfvhlzR+FdGIt
"], "Gun" -> {1970, 1970, 1971, 1990, 1990, 1991, 1991, 1991, 1994, 
     1994, 1995, 1996, 1996, 1996, 1996, 1996, 1997, 1997, 1997, 1997,
      2000, 2003, 2003, 2003, 2004, 2009, 2009, 2009, 2010, 2013, 
     2013, 2013, 2015, 2016, 2017, 2017, 2018, 2018, 2018, 2018, 2020,
      2021, 2021, 2021, 2021, 2022, 2022, 2022, 2022, 2022, 2022, 
     2022, 2022, 2022, 2023, 2023, 2023, 2023, 2023, 2024, 2024, 2024,
      2024}, "Puffer" -> {1971, 1971, 1971, 1971, 1984, 1992, 1992, 
     1993, 1993, 2001, 2001, 2010, 2014, 2014, 2015, 2016, 2022, 
     2022}, "Conduit" -> {1972, 1995, 1996, 1996, 1996, 1996, 1996, 
     1996, 1996, 1996, 1996, 1996, 1996, 1996, 1996, 1996, 1997, 1997,
      1997, 1997, 1997, 1997, 1997, 1997, 1997, 1997, 1997, 1998, 
     1998, 1998, 1998, 1998, 2005, 2006, 2006, 2011, 2011, 2011, 2012,
      2013, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 
     2015, 2015, 2015, 2015, 2015, 2016, 2017, 2018, 2018, 2019, 2020,
      2021, 2022, 2022, 2022, 2022, 2022, 2023, 2024, 2024, 2024, 
     2024}, "Reflector" -> {1993, 1994, 1998, 1998, 1998, 1998, 1998, 
     2001, 2002, 2009, 2009, 2012, 2013, 2013, 2016, 2016, 2016, 2016,
      2016, 2016, 2016, 2016, 2017, 2017, 2017, 2017, 2017, 2017, 
     2017, 2018, 2018, 2018, 2018, 2020, 2021, 2022, 2023, 2023}|>;
decompressedData = 
  KeyValueMap[#1 -> 
     If[Head[#2] === CompressedData, Uncompress[#2], #2] &, data];
boxPlot = 
  BoxWhiskerChart[Values[decompressedData], 
   ChartLabels -> Keys[decompressedData], PlotRange -> {1969, 2025}, 
   GridLines -> {None, Automatic}, ChartStyle -> "Pastel", 
   PlotLabel -> "Year Distribution by Pattern Type", ImageSize -> 600,
    AspectRatio -> 1/2];
iys = Table[
   "In year " <> ToString[year] <> 
    " we discover and construct patterns", {year, 2025, 2018, -1}];
counts = {StringCount[#, "discover" | "use"], 
     StringCount[#, "construct"]} & /@ iys;
years = Range[2025, 2018, -1];
Grid[{{boxPlot}}, Spacings -> {0, 30}]

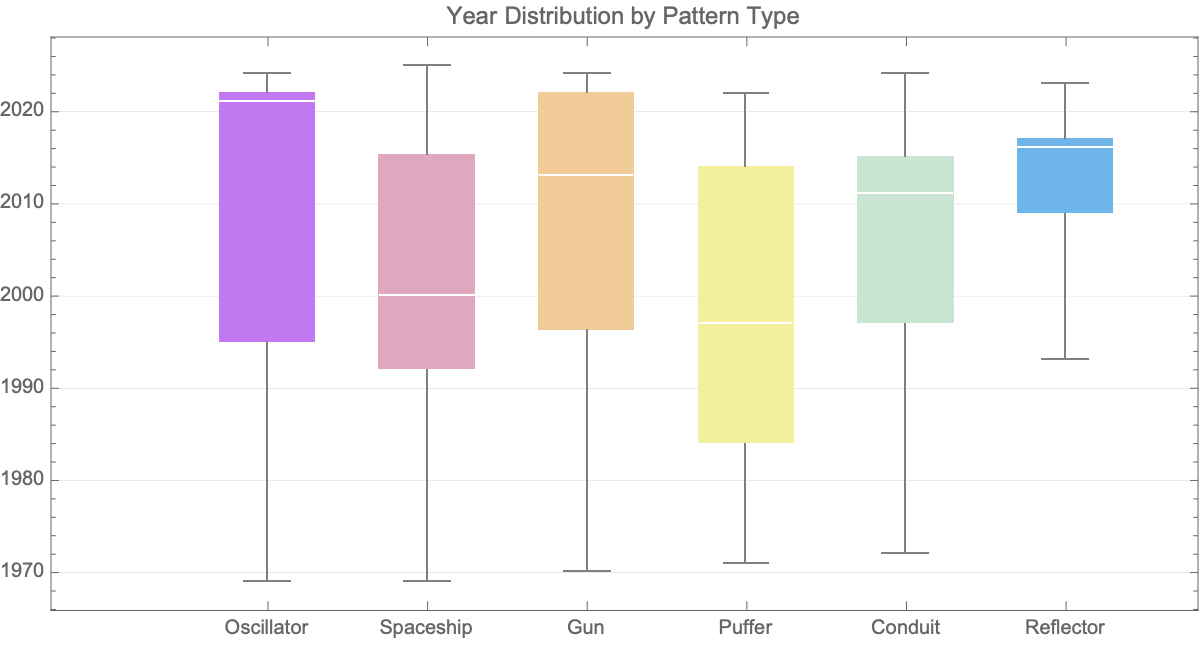
Year Dist

It's the story of a combination of sophisticated visualization techniques, interactive simulations, and historical data analysis, for which the simulated Mathematica approach presents a powerful educational and research tool. Conway's Game of Life has such enduring power and appeal because of the in-depth behavior of cellular automata, because of the continuous avenues for advanced computational discovery of patterns.

POSTED BY: Dean Gladish
Chase Marangu
Chase Marangu
Posted 1 month ago

Amazing Dean Gladish! You go really into depth in this!
POSTED BY: Chase Marangu
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard