Hi,
there are quite some issues with that. First of all there are many free parameters such
$b, N0, \alpha$. To integrate numerically you need to substitute values for them (or use ParametricNDSolve). Syntax that produces an output is:
sols = NDSolve[{\[Pi]^4 Y[y] - b^4 N0 (Y^\[Prime]\[Prime])[y] -
2 b^2 \[Pi]^2 (Y^\[Prime]\[Prime])[y] +
b^3 N0 y \[Alpha] (Y^\[Prime]\[Prime])[y] +
b^4 D[Y[y], {y, 4}] == 0 /. {b -> 1., N0 -> 1, \[Alpha] -> 1},
Y[0] == 0, Y[1] == 0, Y''[0] == 0, Y''[1] == 0}, Y[y], {y, 0, 1}]
There might be some numerical issues though because
Plot[Y[y] /. sols, {y, 0, 1}]
gives
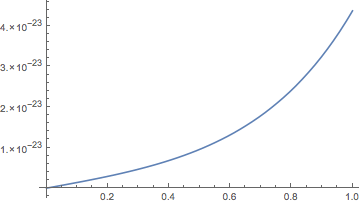
which is numerically zero, where it should be plainly zero. You can fix this by setting a higher Accuracy Goal:
sols = NDSolve[{\[Pi]^4 Y[y] - b^4 N0 (Y^\[Prime]\[Prime])[y] -
2 b^2 \[Pi]^2 (Y^\[Prime]\[Prime])[y] +
b^3 N0 y \[Alpha] (Y^\[Prime]\[Prime])[y] +
b^4 D[Y[y], {y, 4}] == 0 /. {b -> 1., N0 -> 1, \[Alpha] -> 1},
Y[0] == 0, Y[1] == 0, Y''[0] == 0, Y''[1] == 0}, Y[y], {y, 0, 1},
AccuracyGoal -> 100]
That gives a flatline zero.
Cheers,
Marco