Hi,

there are quite some issues with that. First of all there are many free parameters such $b, N0, \alpha$. To integrate numerically you need to substitute values for them (or use ParametricNDSolve). Syntax that produces an output is:

sols = NDSolve[{\[Pi]^4 Y[y] - b^4 N0 (Y^\[Prime]\[Prime])[y] - 
      2 b^2 \[Pi]^2 (Y^\[Prime]\[Prime])[y] + 
      b^3 N0 y \[Alpha] (Y^\[Prime]\[Prime])[y] + 
      b^4 D[Y[y], {y, 4}] == 0 /. {b -> 1., N0 -> 1, \[Alpha] -> 1},
   Y[0] == 0, Y[1] == 0, Y''[0] == 0, Y''[1] == 0}, Y[y], {y, 0, 1}]

There might be some numerical issues though because

Plot[Y[y] /. sols, {y, 0, 1}]

gives

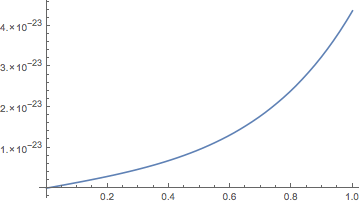
which is numerically zero, where it should be plainly zero. You can fix this by setting a higher Accuracy Goal:

sols = NDSolve[{\[Pi]^4 Y[y] - b^4 N0 (Y^\[Prime]\[Prime])[y] - 
      2 b^2 \[Pi]^2 (Y^\[Prime]\[Prime])[y] + 
      b^3 N0 y \[Alpha] (Y^\[Prime]\[Prime])[y] + 
      b^4 D[Y[y], {y, 4}] == 0 /. {b -> 1., N0 -> 1, \[Alpha] -> 1},
   Y[0] == 0, Y[1] == 0, Y''[0] == 0, Y''[1] == 0}, Y[y], {y, 0, 1}, 
  AccuracyGoal -> 100]

That gives a flatline zero.

Cheers,

Marco

But all the deviations from zero that you see, are only numerical artefacts, aren't they?

sols = ParametricNDSolve[{\[Pi]^4 Y[y] - 
     b^4 N0 (Y^\[Prime]\[Prime])[y] - 
     2 b^2 \[Pi]^2 (Y^\[Prime]\[Prime])[y] + 
     b^3 N0 y \[Alpha] (Y^\[Prime]\[Prime])[y] + 
     b^4 D[Y[y], {y, 4}] == 0,
   Y[0] == 0, Y[1] == 0, Y''[0] == 0, Y''[1] == 0}, 
  Y, {y, 0, 1}, {N0, b, \[Alpha]}, AccuracyGoal -> 100]

gives

I suppose that the existence and uniqueness theorem would suggest that there is only one solution, which is the "trivial" solution?

Cheers,

M.

PS: Another clue that the solutions that deviate from zero cannot be accurate is that they do not fulfil one of the boundary conditions, i.e. Y[1]==0.

Thank you very much. I did not know about "AccuracyGoal". I'm solving an equation of elastic buckling of rectangular plate with linearly varying in-plane load and I expected the solution similar to Y[y] = Sin[[Pi]*y/b]. This is the solution of my equation if [Alpha] = 0 and load is constant. I expected solution similar to the last picture.