I assume you have generated the graph from a list of points. If so, then perhaps the best place to start is with a function that acts on a set of 2-dimenstional cartesian coordinates and determines the ones that are within a circle of radius r.

Let's say you have a bunch of points specified by their {x,y} coordinates. Here is an example of some random points within a square centered at the origin with sides of length 20 :

In[1]:= myPoints = RandomReal[{-10, 10}, {10, 2}]

Out[1]= {{9.46899, 0.761273}, {-6.23467, 0.511913}, {7.35649, 
  2.65914}, {2.29141, -4.28594}, {-1.70496, 0.849794}, {5.71018, 
  2.75263}, {3.8676, 3.89367}, {-2.3946, 
  8.70738}, {2.98544, -8.53176}, {-5.03731, -0.288273}}

Then the points contained within a circle of radius r can be determined by using the following function or something like it:

pointsInR[points : {{_, _} ..}, r_ /; r > 0] := Select[points, Sqrt[#.#] < r &]

Let's try it out:

In[5]:= pointsInR[myPoints, 8]

Out[5]= {{-6.23467, 0.511913}, {7.35649, 
  2.65914}, {2.29141, -4.28594}, {-1.70496, 0.849794}, {5.71018, 
  2.75263}, {3.8676, 3.89367}, {-5.03731, -0.288273}}

And the number of points within a radius r is given by the Length of this list:

In[9]:= Length[pointsInR[myPoints, 8]]

Out[9]= 7

And

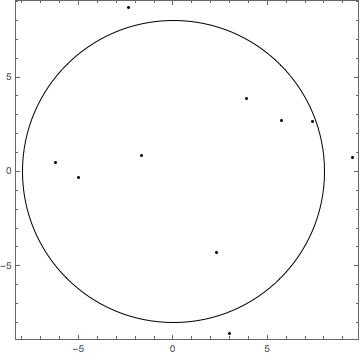
Graphics[{Point[myPoints], Circle[{0, 0}, 8]}, Frame -> True]

Gives

Sure. I threw some of that in there in case you were not familiar with them so you could ask ;-)

In the left hand side of the function definition

pointsInR[points : {{_, _} ..}, r_ /; r > 0]

the

points : {{_, _} ..}

is indicating that the first argument, points, should have the pattern (http://reference.wolfram.com/language/tutorial/PatternsOverview.html) where it is a list of lists, each of which is a pair of values -- i.e., a list of cartesian pairs to comprise the coordinates of the points. It just restricts the function to only working when such a pattern is supplied. If you don't supply that pattern then the function will return unevaluated.

In a similar way, the second argument pattern

r_ /; r > 0

is just demanding that the radius argument be greater than zero--a sensible argument constraint given that the radius should be positive for the circle.

I could have written the function simply like this:

pointsInR[points_, r_] := Select[points, Sqrt[#.#] < r &]

but then, if you give it arguments of the wrong form, all sorts of havoc might be the result.

The

Sqrt[#.#] < r &

is an example of a pure function:

http://reference.wolfram.com/language/tutorial/PureFunctions.html

It is a way of defining a function to be used without having to name it. David Keith similarly uses a pure function in his discussion.

The # and the & are a shorthand for implementing a pure function. Another way of writing this, using the full Function form would be

Function[z,Sqrt[z.z] < r ]

I understand that this may give you a bunch of stuff to chew on, but it will be well worth learning these bits.

I hope this helps.