There was an article published recently, but I can't find it here. Someone in the social sciences at a university was accused of cooking his results. Both sides are now claiming that they are blameless and the other is at fault. Somehow a side effect of this was a substantial effort to carefully replicate a few dozen major long accepted classical results in the field. Approximately one third of the replications either failed to support the hypothesis or had sufficiently serious problems with the experiment that no claim could be made. In every case mentioned the original experimenter is furious that they have been targeted by a witch hunt, their reputation has been permanently damaged, they have no way of defending themselves and nothing can be done to make up for this. You should track down the original source of this before using it, just to make certain that I have not somehow skewed the claims. It might have been published in Science in 2013, but I can't be sure.

If the likes of Tufte's standards could begin to make it the norm that uncertainty be clearly shown with every claim and Mathematica could position itself as one of the leading tools to simply and easily produce graphics for claims then, as mentioned above, perhaps everyone might be in a slightly better position to see at a glance what has sufficiently small uncertainty to likely be accepted and what has so much uncertainty that it can be dismissed.

Bill, that seems a bit off topic of whether academics are missing out by not making greater use of Mathematica. But maybe not completely. Because of their active and dynamic character, Mathematica provides the opportunity of presenting higher quality results with higher integrity. One can include, in the document, raw data and procedures for analyzing and representing the results. Others can check if they actually work or have entry points for exposing problems. If people want to lie about data I suppose they can but it's not quite as easy to get by with just plain sloppiness.

I once worked as a computer consultant for a group of biochemists. At one point I was asked to look at an experiment one of them was doing to measure the rate of some biochemical reaction. The person was very nice and very meticulous in his biochemistry. But when I looked at the reaction system and what he was measuring I discovered to my horror that it had no relation at all to the reaction rate he was trying to measure. Needless to say, he was not pleased with this. I left the group but later learned from someone who replaced me that they continued the experiment and analyzed it with a statistical program. The result was something like 1.0 +/- 10^6 millimole/minute - and they published it!

Bill, your remarks are well put. I think that Tufte somewhere does have a maxim to Be Honest. And he does give several suggestions in Visual Explanations page 34. This might include multiple presentations based on different measures or viewpoints and textual explanation that might address various concerns. That's why I'm an advocate of literate notebooks that make a case and try to clarify and present a true picture. I would be very skeptical of any analysis summarized in a single presentation without extended discussion. In the final analysis it largely depends on the integrity of the person making or responsible for the analysis.

Mathematica probably has the tools to present uncertainty and risk. You just have to figure out how to put them together. With a dynamic presentation you can provide information in tooltips. You can provide information in numerical side reports, which may vary as you move a locator about the primary data representation. You might be able to toggle a presentation between various assumptions. And of course there are the old fashioned error bars and multiple presentations. Your suggestion of fuzzing the data representation might work very well. To go one step further, in a Mathematica notebook (or application) you can give the reader active tools for performing various types of data reduction and the actual data itself. I'm not knowledgeable about statistical analysis of data; I'm sure you can work out much better methods. The point is: Mathematica does give you better tools to present honest results.

I first used Macsyma over a 300 baud modem over the Arpanet from Caltech to MIT back in the mid 70s. And I found a bug. They had the general solution to the cubic entered incorrectly.

"All of the manuals on how to use Mathematica have been written by people who know too much. Their work should be edited by someone like me who is trying to learn what the developers already know."

Luther, I find your basic thesis here by and large accurate. Mathematica does have a steep learning curve and to directly use the more advanced features (particularly the various programming paradigms) one has to think like Mathematica, which for me has not come naturally.

Like others here, I started off with FORTRAN punch cards in college and was simply amazed at what could be done with the "simple" Do Loop. Ten or so years later I stumbled upon Macsyma, anybody remember that ? It was a command line math tool that claimed it could do symbolic math, maybe it could but I did not find it useful. Then I noticed that our Technical Librarian had a copy of Mathematica sitting on her shelf, version 2.2. After inquiring about it I learned that one of the Chief Engineers owned it originally but returned it to her because he couldn't figure out how to use it. I convinced my company to purchase the Premier Support package which offers supurb technical support and over the years would amaze him (and myself) of what could be done with this tool. I also read a few Mathematica books which I enjoyed at the time but that didn't boost my usability knowledge as I had hoped. During and prior to these years I became somewhat proficient with FORTRAN, MathCad, Excel, BASIC, Minitab and Matlab. And from my experience only Matlab comes close to the power of Mathematica if various toolboxes were acquired. Out of the box, Mathematica was a clear winner for my technical computing and data processing needs. And when serious statistics were added (ver 8 I think) there was no need for any other tool.

Fast forward to today, I am still a clunky Mathematica user and I still rely on the basic Do Loop from yesteryear even though much more efficient programming techniques have been available in Mathematica for years. But I've done some pretty neat stuff that no one else in the company has been able to do.

I share the learning curve frustration but I will take a hard to use yet capable tool over an easy to use limited tool any day. And for my technical computing needs, Mathematica has never let me down in the sense that if I could conceive it, Mathematica could be coaxed to solve it; that is powerful.

On a practical note, the approach I have found very useful is to create and maintain a private library of "How To Notebooks" that describe a narrow task that you know you will be facing again in the future. The source material for these may come from the hard slugging and self-learning that you have produced, a call to Tech Support , the online Help, books, or the Mathematica StackExchange site. If I look at my "How To" Folder I see file names like

How to align entries nicely using TableForm.nb How to compute running averages.nb How to conditionally extract values from a list.nb How to convert time formatted strings to numerical values.nb How to control minor ticks on a log axis.nb How to create a 3-D surface plot.nb How to extract algebraic solutions produced by the Solve command.nb etc.

I find this is far more useful that trying to rely on the built-in Help which, in general, offers a very simple example or two (material that you already know) and then jumps to examples so complex that [literally] some Tech Support Engineers at Wolfram have had some difficulty with, and these guys are good !

Kudos to Stephen Wolfram and his team for inventing, enhancing and maintaining what I think is the strongest technical computing environment on the planet. The professors mentioned at the beginning of this discussion don't know what they are missing.

For an example, that I have put to use in my own work, Google and download the Sandia report Sample Sizes for Confidence Limits and Reliability, by J. Darby.

Hello, Yes, the "symbolic-program-x" I referred to above was Macsyma as well (I thought the general rule here was not to mention other software by name? Or, perhaps that was the mathgroup newsgroup?)

Back towards the original topic. I am thinking about the ways that I use Mathematica. They don't fit easily into a single category. Mathematica is something of a swiss army knife.

Academics have less time on their hands than many people think--most of my faculty colleagues work long (and thankless) hours seven days a week. And, I believe that, in most cases, the time is not spent on research or teaching. So, I was wondering why I am able to open Mathematica at all?

From a research perspective, I use Mathematica:

1) derive stuff

2) simulate stuff

2) keep track of stuff that I've derived

3) visualize things that I've learned.

It serves as workbench and as scratch paper. As much as I agree with David Park's viewpoint about using Mathematica to publish, I can't afford for the research community to catch up or adopt. It's a battle that I can't win and I'm either too afraid or too lazy to fight. However, It is easy and eye-opening to give presentations with Mathematica--hopefully this might help get the ball rolling to archival publication.

From a teaching perspective, I use Mathematica:

1) To show students that they can understand a physical phenomenon much much better by coding it and visualizing it.

2) to reduce the barrier for physical scientists to learning maths that they should know (the documentation and electronic communities are excellent modules for math as well as mathematica).

3) simulating physical systems for pedagogy.

I believe that being able to code is integral to scientific literacy. For physical scientists, symbolic computing languages like Mathematica threads together many educational goals.

From a recreational perspective,

1) It is fun just to play with new ideas by coding them up.

2) I have collaborated on pieces that have been exhibited at MoMA, the Pompidou, the Paris Fashion Show, and other places that we created with Mathematica.

Finally, while we are quoting about death and revolution, there is a nice one by Henry Ford, "“Anyone who stops learning is old, whether at twenty or eighty. Anyone who keeps learning stays young.” Just playing with Mathematica is a good strategy for staying young.

I basically use Mathematica for all my work unless otherwise forced asunder. I write all my documents in it and have done since around version 3 (when the typesetting became publication class).

I think it was either Planck or Boltzmann who said that progress in Physics is made at funerals. You advance a new theory or process and wait for the old physicists to die. Having a Ph.D. in Physics myself, I'm allowed to say this. It's probably true for almost all fields of human endeavor.

I would like to weigh in here even though I'm not an academic, because it's a topic dear to my heart. I think the most valid complaint on Craig's list is number 2. Here's the test: How much time is spent in doing the math and science and how much time in trying to coerce Mathematica into doing what you want? If it tilts too much to the latter Mathematica will lose.

Nevertheless, Mathematica has tremendous advantages, which many academics and users seem to be unaware of and which are basically out-of-sight. It could and should be the premiere publication medium for technical (and maybe even a lot of non-technical) material. It should blow LaTex and PDF documents out of the water. This is because of the active and dynamic capabilities of Mathematica notebooks (and CDF documents): the ability to transmit usable routines with the documents, and the ability to accumulate capability in a documented form, not to speak of all the capability built into Mathematica itself.

And yet, Mathematica has completely failed at this. Look at arXiv.org. How many Mathematica notebooks will you find? I haven't tried to check or search all entries but it looks like the score is something like LaTex/PDF 1,000,000, Mathematica notebooks 0. (Of course, some of the PDF's have graphics or mathematical results copied from Mathematica.) So how many academics even see examples of what can be done?

Academics need a positive reason to switch to Mathematica for routine work. There are plenty of very good reasons. They just don't see them.

On the other hand, the second item on Craig's list is quite important. Mathematica is difficult to use. Wolfram Research has not made sufficient effort in usability. Their approach has been to add more bells and whistles and top-down routines. This only makes usage more difficult. Often you may find that you have to modify a high level routine, generally using options or special constructions, to get what you want - only to find out after several hours that it can't be done. It would be much simpler if, as much as possible, capability was built from the bottom up and made available to the user. It's all right to offer some common high level routines (built from the lower level objects) but the user should always have the option to fall back to the more primitive constructions.

For graphics and dynamic displays, the paradigm should be "writing on a piece of paper". That's what academics do all the time. They kind of understand that. In part, that means separating the calculation from the writing.

Another difficulty is that this active and dynamic medium is quite new and revolutionary. Even if Mathematica were easy to use, it's still not all that clear or simple to know the best usage. It's easy to fill displays with "computer junk". Just taking a 19th or 20th century diagram and making something move is not necessarily very informative. There are many possibilities and matters of taste that need to be creatively explored. This is why WRI has to leave the user free to write displays adapted to special cases at hand. They can't even come close to anticipating what form these might take - or providing high level routines for them.

Finally, I would like to include two display examples, which Mathematica's high level routines are not particularly good at doing. I didn't use standard methods for either of these and yet they should be the kind of thing that would be reasonably easy to do,

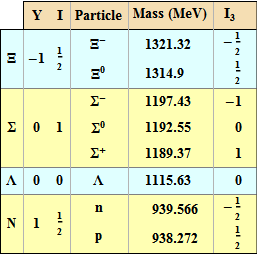
The following is adapted from the first table I found in Arfken & Weber, Mathematical Methods for Physics, Fifth Edition, 2001, Academic Press. The original was somewhat confusing. This was composed using a set of routines that allow me to write information and formatting directly on a "piece of paper" without using the rather complicate options in Grid. Would you find it easy to compose this using Grid? Does technical work ever use custom tables?

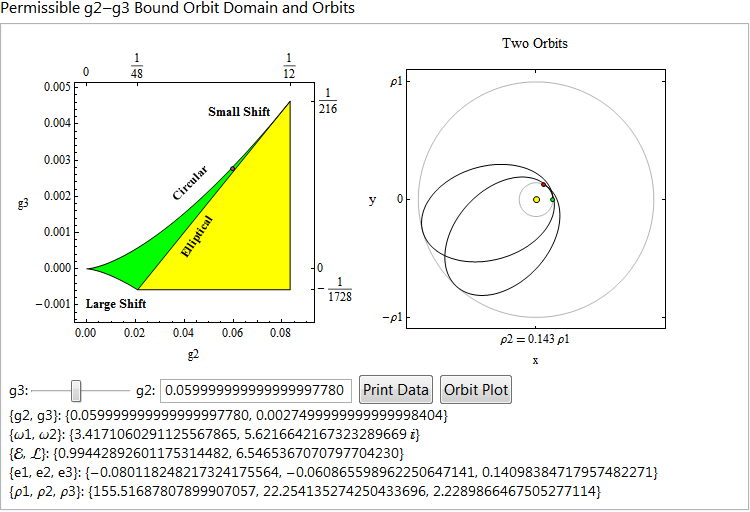
The second example is from a notebook on the use of the Weierstrass elliptic P function in representing EXACT solutions of orbits in the Schwarzschild geometry. I was introduced to this by Ron Burns. This was done using a DynamicModule. I never use the Manipulate statement. I find it too difficult to con out its behavior and I want to arrange the layout just the way I want. The Weierstrass function is characterized by two parameters, g2 and g3, and the green region shows the domain for bound orbits. The region is a thin wedge where most of the physical cases occur. The g3 Slider is dynamically adapted to this and varies only across the green domain - the variation is in the 5th or 6th place. Even though the Weierstrass function was known well before Einstein and Schwarzschild, not to speak of Misner, Thorn and Wheeler, the high precision required probably mitigated against its use. But you can see that I used quite high precision and Mathematica had no difficulty with it at all. That might be one powerful reason in favor of Mathematica.

Luther, why don't you write me at djmpark@comcast.net and tell me what your project is.

Probably not what you had but maybe related:

http://library.wolfram.com/infocenter/Conferences/5782/

This is by Paul Wellin and he may have been author or a coauthor of the work you have in mind.

Dear Luther, I've been puzzling over your observation for nearly 15 years, and I also fail to understand why Mathematica/Wolfram Language gets dismissed by my colleagues so haphazardly. In discussions with my colleagues about this question, I tend to go in listening mode and don't advocate on one side or another. I'll try to summarize what they say below.

Some background:

I'm a professor at MIT in physical sciences and engineering. I've been teaching a course on mathematics and problem solving in materials science for about twelve years, and I use Mathematica extensively in my course. I can't judge the efficacy of my course objectively, but my students generally have very positive evaluations; I've been given MIT's highest institutional teaching awards, as well as the School of Engineering's. I believe that these awards reflect the quality of the Mathematica based course. I give nearly all of my research presentations using Mathematica and these are received well (however, such feedback tends to be biased towards positive)

The summary (I don't agree with many of these, and am still honing my counter arguments)

1) Mathematica is not as fast as X (X may or may not be a compiled language).

2) Mathematica's syntax creates too steep of a learning curve.

3) Our (particular) scientific community uses X; so there are many more routines and working examples in X

4) I am already using X, why should I change?

I believe most of the above are the result of "user inertia".

I don't hear the comment that Mathematica gives "bad results" so much now. I doubt if many faculty roll their own algorithms, but are probably thinking back to when they were postdocs or graduate students--however, there are happy exceptions to this

I believe that the best way forward is to offer students a choice; and hope that they will make an unfettered choice of a their preferred programming language. However, I am not so optimistic: a student who went to graduate school at a university down the street wrote to me saying, "I'm taking this class and they insist on using X and I asked if I could use Mathematica instead, and he said no. We were doing more advanced things in 3.016 ( the sophomore class I teach)."

"starting with my first job at Michigan (we used a Wang with punch cards!!!)"

Around 1982 I had a job overhauling a Wang Fortran compiler (the project name was, not surprisingly, WANGFOR). I also was requested to augment in terms of functionality, the so-called "Wang enhancement" project (WANGENH). (No, I'm not making this up. Not even the project names. It was a Fortran-66 compiler and they wanted to add some of the Fortran-77 capabilities, if I recall correctly.)

My company and Wang Labs had a falling out several months later and, as best I can tell, mutually fired one another. But the work on that decrepit compiler was, I think, pretty good.

So this makes two of us who worked with Wang's Fortran. Also their assembler code, in my case.

Ah, memories!