I would like to weigh in here even though I'm not an academic, because it's a topic dear to my heart. I think the most valid complaint on Craig's list is number 2. Here's the test: How much time is spent in doing the math and science and how much time in trying to coerce Mathematica into doing what you want? If it tilts too much to the latter Mathematica will lose.

Nevertheless, Mathematica has tremendous advantages, which many academics and users seem to be unaware of and which are basically out-of-sight. It could and should be the premiere publication medium for technical (and maybe even a lot of non-technical) material. It should blow LaTex and PDF documents out of the water. This is because of the active and dynamic capabilities of Mathematica notebooks (and CDF documents): the ability to transmit usable routines with the documents, and the ability to accumulate capability in a documented form, not to speak of all the capability built into Mathematica itself.

And yet, Mathematica has completely failed at this. Look at arXiv.org. How many Mathematica notebooks will you find? I haven't tried to check or search all entries but it looks like the score is something like LaTex/PDF 1,000,000, Mathematica notebooks 0. (Of course, some of the PDF's have graphics or mathematical results copied from Mathematica.) So how many academics even see examples of what can be done?

Academics need a positive reason to switch to Mathematica for routine work. There are plenty of very good reasons. They just don't see them.

On the other hand, the second item on Craig's list is quite important. Mathematica is difficult to use. Wolfram Research has not made sufficient effort in usability. Their approach has been to add more bells and whistles and top-down routines. This only makes usage more difficult. Often you may find that you have to modify a high level routine, generally using options or special constructions, to get what you want - only to find out after several hours that it can't be done. It would be much simpler if, as much as possible, capability was built from the bottom up and made available to the user. It's all right to offer some common high level routines (built from the lower level objects) but the user should always have the option to fall back to the more primitive constructions.

For graphics and dynamic displays, the paradigm should be "writing on a piece of paper". That's what academics do all the time. They kind of understand that. In part, that means separating the calculation from the writing.

Another difficulty is that this active and dynamic medium is quite new and revolutionary. Even if Mathematica were easy to use, it's still not all that clear or simple to know the best usage. It's easy to fill displays with "computer junk". Just taking a 19th or 20th century diagram and making something move is not necessarily very informative. There are many possibilities and matters of taste that need to be creatively explored. This is why WRI has to leave the user free to write displays adapted to special cases at hand. They can't even come close to anticipating what form these might take - or providing high level routines for them.

Finally, I would like to include two display examples, which Mathematica's high level routines are not particularly good at doing. I didn't use standard methods for either of these and yet they should be the kind of thing that would be reasonably easy to do,

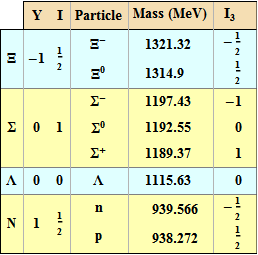
The following is adapted from the first table I found in Arfken & Weber, Mathematical Methods for Physics, Fifth Edition, 2001, Academic Press. The original was somewhat confusing. This was composed using a set of routines that allow me to write information and formatting directly on a "piece of paper" without using the rather complicate options in Grid. Would you find it easy to compose this using Grid? Does technical work ever use custom tables?

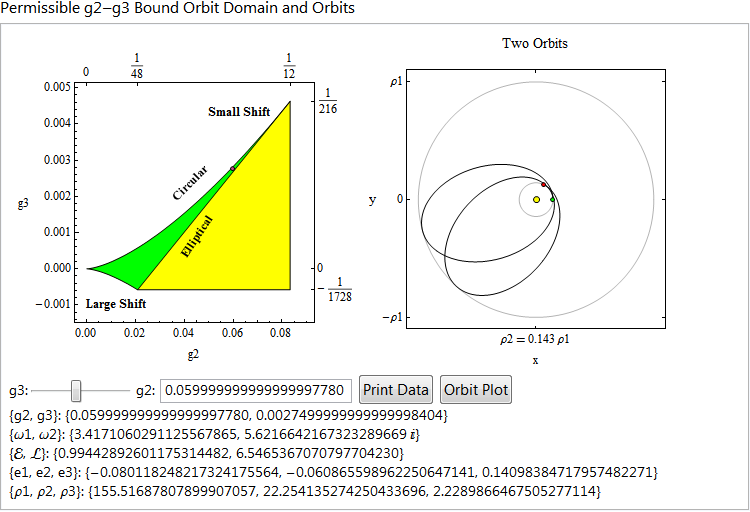
The second example is from a notebook on the use of the Weierstrass elliptic P function in representing EXACT solutions of orbits in the Schwarzschild geometry. I was introduced to this by Ron Burns. This was done using a DynamicModule. I never use the Manipulate statement. I find it too difficult to con out its behavior and I want to arrange the layout just the way I want. The Weierstrass function is characterized by two parameters, g2 and g3, and the green region shows the domain for bound orbits. The region is a thin wedge where most of the physical cases occur. The g3 Slider is dynamically adapted to this and varies only across the green domain - the variation is in the 5th or 6th place. Even though the Weierstrass function was known well before Einstein and Schwarzschild, not to speak of Misner, Thorn and Wheeler, the high precision required probably mitigated against its use. But you can see that I used quite high precision and Mathematica had no difficulty with it at all. That might be one powerful reason in favor of Mathematica.

"All of the manuals on how to use Mathematica have been written by people who know too much. Their work should be edited by someone like me who is trying to learn what the developers already know."

Luther, I find your basic thesis here by and large accurate. Mathematica does have a steep learning curve and to directly use the more advanced features (particularly the various programming paradigms) one has to think like Mathematica, which for me has not come naturally.

Like others here, I started off with FORTRAN punch cards in college and was simply amazed at what could be done with the "simple" Do Loop. Ten or so years later I stumbled upon Macsyma, anybody remember that ? It was a command line math tool that claimed it could do symbolic math, maybe it could but I did not find it useful. Then I noticed that our Technical Librarian had a copy of Mathematica sitting on her shelf, version 2.2. After inquiring about it I learned that one of the Chief Engineers owned it originally but returned it to her because he couldn't figure out how to use it. I convinced my company to purchase the Premier Support package which offers supurb technical support and over the years would amaze him (and myself) of what could be done with this tool. I also read a few Mathematica books which I enjoyed at the time but that didn't boost my usability knowledge as I had hoped. During and prior to these years I became somewhat proficient with FORTRAN, MathCad, Excel, BASIC, Minitab and Matlab. And from my experience only Matlab comes close to the power of Mathematica if various toolboxes were acquired. Out of the box, Mathematica was a clear winner for my technical computing and data processing needs. And when serious statistics were added (ver 8 I think) there was no need for any other tool.

Fast forward to today, I am still a clunky Mathematica user and I still rely on the basic Do Loop from yesteryear even though much more efficient programming techniques have been available in Mathematica for years. But I've done some pretty neat stuff that no one else in the company has been able to do.

I share the learning curve frustration but I will take a hard to use yet capable tool over an easy to use limited tool any day. And for my technical computing needs, Mathematica has never let me down in the sense that if I could conceive it, Mathematica could be coaxed to solve it; that is powerful.

On a practical note, the approach I have found very useful is to create and maintain a private library of "How To Notebooks" that describe a narrow task that you know you will be facing again in the future. The source material for these may come from the hard slugging and self-learning that you have produced, a call to Tech Support , the online Help, books, or the Mathematica StackExchange site. If I look at my "How To" Folder I see file names like

How to align entries nicely using TableForm.nb How to compute running averages.nb How to conditionally extract values from a list.nb How to convert time formatted strings to numerical values.nb How to control minor ticks on a log axis.nb How to create a 3-D surface plot.nb How to extract algebraic solutions produced by the Solve command.nb etc.

I find this is far more useful that trying to rely on the built-in Help which, in general, offers a very simple example or two (material that you already know) and then jumps to examples so complex that [literally] some Tech Support Engineers at Wolfram have had some difficulty with, and these guys are good !

Kudos to Stephen Wolfram and his team for inventing, enhancing and maintaining what I think is the strongest technical computing environment on the planet. The professors mentioned at the beginning of this discussion don't know what they are missing.

For an example, that I have put to use in my own work, Google and download the Sandia report Sample Sizes for Confidence Limits and Reliability, by J. Darby.

"starting with my first job at Michigan (we used a Wang with punch cards!!!)"

Around 1982 I had a job overhauling a Wang Fortran compiler (the project name was, not surprisingly, WANGFOR). I also was requested to augment in terms of functionality, the so-called "Wang enhancement" project (WANGENH). (No, I'm not making this up. Not even the project names. It was a Fortran-66 compiler and they wanted to add some of the Fortran-77 capabilities, if I recall correctly.)

My company and Wang Labs had a falling out several months later and, as best I can tell, mutually fired one another. But the work on that decrepit compiler was, I think, pretty good.

So this makes two of us who worked with Wang's Fortran. Also their assembler code, in my case.

I basically use Mathematica for all my work unless otherwise forced asunder. I write all my documents in it and have done since around version 3 (when the typesetting became publication class).

Some comments on "attitude" and "culture". One of the greatest influences on me have been the books on data graphics by Edward Tufte. It is one reason I believe in writing literate notebooks with textual explanations and multiple and carefully designed presentations. Tufte writes: " Those who discover an explanation are often those who construct its representation." Mathematica gives you plenty of tools for constructing representations and exploring their behavior.

And why textual explanation? Because if you can't give a simple clear explanation it should leave you a bit skeptical as to your level of understanding. The same goes for documentation of a routine. If it's difficult to document maybe it should be redesigned or scrapped for some other routine. Textual explanation and documentation are not onerous chores, they are part of the learning or creative process.

I tend to eschew the terms "code" and "programming" in favor of terms such as "writing definitions, axioms, rules and specifications". After all, we're trying to do math and science. WRI can hire the programmers. It's a matter of attitude and culture.

Lots of people in academia write papers and even books as part of the process of better learning the material. Do you think they always knew it all before they started? So even if it's self-study, writing literate notebooks is good practice. And they might very well be good enough to interest other people. The same applies to having students write literate notebooks, even if they are relatively short. When they're finished they actually have something to show off. Science and technology are no good if they can't be communicated.

Also, if students can design new and clear presentations along with explanations, they are not only learning but they are adding value because these do not always exist together now.

And thanks to Luther for starting this discussion.

Clearly, that is something I have to start doing.

That was possibly a bug, so to speak, in the CRC reference at the time. It did not really account for choices of roots used, at least in the quartic formula. This may also have been an issue with the cubic. This was stuff I had to work through in 1992.

Probably not what you had but maybe related:

http://library.wolfram.com/infocenter/Conferences/5782/

This is by Paul Wellin and he may have been author or a coauthor of the work you have in mind.

This is not intended to criticize Edward Tufte or diminish any of the fine work he has done. If you carefully study each of his books you might notice that there is one thing which has not been included. There is not a hint of uncertainty in any of the graphics that he presents. For one example, I cannot imagine in the fog of war in 1812 that Napoleon's march on Moscow was anywhere near as precise and tidy as the famous graphic leads our minds to believe. Yes, the graphic does round the numbers to thousands, but even that I suspect is a misrepresentation.

I spent time some years ago trying to get vendors to use all the new found compute power to demand from the user and then display the uncertainty associated with graphical presentations. Yes, Mathematica keeps track of the precision associated with some numeric quantities, but Plot does not then display graphics which are just fuzzy enough to force us to realize how much we don't know. I don't think the classic error bars are the answer, but fuzz might be.

Several simulation tool vendors will quietly admit that their calculations are really not as precise as their tool displays. One vendor even suggested that I diddle the coefficients a little each time, do ten runs, print all the results, tape them to a window and try to guess what the uncertainty really is.

I listened to an invited speaker years ago. He presented slide after slide of very impressive graphics showing the behavior of something. He was asked if it would be possible to include an indication of the uncertainty in his slides. He replied no, because if he did then it would be obvious that his results had no predictive power. I suspect even the audience members who already knew this still made incorrect assumptions when looking at the graphics.

Consider how many predictions we see for projects large and small. We almost never see the uncertainties of the inputs or outputs or any indication of the uncertainty associated with the project success or failure. The only use of uncertainty currently is to claim there is none if it my project or it is a stupid idea and we shouldn't do it if it is yours.

It seems that everyone wants to know "the number", nobody wants to hear there is any uncertainty. Everyone wants to see the graph with the spidery little line showing the economy is going smoothly off to infinity. There was a book not too long ago which talked about how everyone wants to be told the number, usually the mean, and how badly we make mistakes when we don't see and plan for the uncertainties. Ah! Found it! The Flaw of Averages: Why We Underestimate Risk in the Face of Uncertainty by Sam Savage, Jeff Danziger and Harry Markowitz. This should not be license to now have to make up numbers for the uncertainties to go along with the numbers we made up for the predictions.

I considered writing a letter to Mr. Tufte asking him if in his next book he might introduce the world to the knowledge that nothing in the real world is precise, when we don't know the uncertainty that we reach false conclusions and we should all begin demanding credible uncertainty information be included in graphics. But the last word I heard is that he is deep into what will likely be his final book and I doubt that he could incorporate such a dramatic change in presentation now. If Mr. Tufte can't be the one to do this then perhaps someone else can.

Bill, your remarks are well put. I think that Tufte somewhere does have a maxim to Be Honest. And he does give several suggestions in Visual Explanations page 34. This might include multiple presentations based on different measures or viewpoints and textual explanation that might address various concerns. That's why I'm an advocate of literate notebooks that make a case and try to clarify and present a true picture. I would be very skeptical of any analysis summarized in a single presentation without extended discussion. In the final analysis it largely depends on the integrity of the person making or responsible for the analysis.

Mathematica probably has the tools to present uncertainty and risk. You just have to figure out how to put them together. With a dynamic presentation you can provide information in tooltips. You can provide information in numerical side reports, which may vary as you move a locator about the primary data representation. You might be able to toggle a presentation between various assumptions. And of course there are the old fashioned error bars and multiple presentations. Your suggestion of fuzzing the data representation might work very well. To go one step further, in a Mathematica notebook (or application) you can give the reader active tools for performing various types of data reduction and the actual data itself. I'm not knowledgeable about statistical analysis of data; I'm sure you can work out much better methods. The point is: Mathematica does give you better tools to present honest results.

Luther, why don't you write me at djmpark@comcast.net and tell me what your project is.

We have walked the same dusty trail. I had forgotten about Macsyma.

I do some of the things you suggest, but in a less ordered fashion. I have several worksheets that I have input various solutions and approaches to problems, and I just keep using the same worksheets. My memory is good enough that I remember that they are in the worksheets and I open one and start scrolling. I call it my cluttered desktop approach.

I second your admiration for Wolfram. And I will look up the reference you suggested. Thanks.

Hello, Yes, the "symbolic-program-x" I referred to above was Macsyma as well (I thought the general rule here was not to mention other software by name? Or, perhaps that was the mathgroup newsgroup?)

Back towards the original topic. I am thinking about the ways that I use Mathematica. They don't fit easily into a single category. Mathematica is something of a swiss army knife.

Academics have less time on their hands than many people think--most of my faculty colleagues work long (and thankless) hours seven days a week. And, I believe that, in most cases, the time is not spent on research or teaching. So, I was wondering why I am able to open Mathematica at all?

From a research perspective, I use Mathematica:

1) derive stuff

2) simulate stuff

2) keep track of stuff that I've derived

3) visualize things that I've learned.

It serves as workbench and as scratch paper. As much as I agree with David Park's viewpoint about using Mathematica to publish, I can't afford for the research community to catch up or adopt. It's a battle that I can't win and I'm either too afraid or too lazy to fight. However, It is easy and eye-opening to give presentations with Mathematica--hopefully this might help get the ball rolling to archival publication.

From a teaching perspective, I use Mathematica:

1) To show students that they can understand a physical phenomenon much much better by coding it and visualizing it.

2) to reduce the barrier for physical scientists to learning maths that they should know (the documentation and electronic communities are excellent modules for math as well as mathematica).

3) simulating physical systems for pedagogy.

I believe that being able to code is integral to scientific literacy. For physical scientists, symbolic computing languages like Mathematica threads together many educational goals.

From a recreational perspective,

1) It is fun just to play with new ideas by coding them up.

2) I have collaborated on pieces that have been exhibited at MoMA, the Pompidou, the Paris Fashion Show, and other places that we created with Mathematica.

Finally, while we are quoting about death and revolution, there is a nice one by Henry Ford, "“Anyone who stops learning is old, whether at twenty or eighty. Anyone who keeps learning stays young.” Just playing with Mathematica is a good strategy for staying young.

Bill, Bravo. Very well articulated. Thanks.

Sadly, careful error propagation, null hypotheses, standard error and sample sizes, p values, etc are disappearing from the canonical topics of a physical science education, and many papers appear in press with no discussion of error and uncertainty.

The typical excuse for omission is "curriculum pressure". I think we are just not teaching effectively.

Good points and I plead guilty to the leakage observation. I was in the "business" at one time and have seen a variety of cultures at work. My knee jerk was a recollection of the times I was burned as a "customer". Within software developers is an undercurrent of certainty that they know best or, as with many technical people, they come across a better way of doing things while working on some project...so they shift gears without letting anyone know. This is the bane of project managers.

I recall meeting a past graduate school colleague at a conference. He had set up a company that was successful and one of its lines of business was developing specialized scientific analysis software for the DoD in the areas of spectroscopy. We chatted and he discovered I was associating with the same types of customers and developers as he was, so he asked me my opinion on what it would take to commercialize his products for a wider audience. One of my own staff had developed a different type of specialized analysis software and we were wrestling with the same question: how to expand the market for that intellectual property. I had no answer for my friend or myself. Some fifteen or so years later, the software my group had developed did show up as a commercial product developed independently elsewhere, and their secret was the user interfaces and easy of use, which our intellectual property never possessed....nor did we have the capacity to address that issue. Plus, the market for the new product had never occurred to us.

Mathematica's documentation is as good as it has to be for Wolfram not to suffer any commercial consequences. Wolfram is blessed by an outstanding product and a user community that is so smart that it overcome the deficiencies in the documentation...plus, to be crass about it, Wolfram sells support services. I think where Wolfram may be somewhat short sighted is that such issues as are being raised in this thread indicates that they could promote a ground swell of broader acceptance and use by "commoditizing" their product. This is just the businessman in me speaking. I would reject the idea of a slimmed down or crippled version just to get a cheaper product out, but too many bells and hidden whistles is pretty frustrating in any product. As an example, I just bought a new phone that uses Android and I tried to set up my voice mail account. I had to go on-line to find someone to tell me where the set up was hidden and it was definitely hidden. The documentation did not even address voice mail but it supplied overkill (from my perspective) in the areas of applications and data.

Mathematica is what it is and from a commercial perspective, Wolfram is doing what it needs to do to stay on top of their game...they have a business strategy that does not depend on better transparent documentation. Mathematica is the best mousetrap around from my perspective. Could it be better? Probably, but define better.