Curiously enough I have just seen this recent article published - also about Montana, Mathematica and the shortest path:

All 56: Solving Montana's 'traveling salesman' problem

Dear Vitaliy,

I wonder whether it would be nice to use Tooltip to add photos of the markers that show the parks. I thought that one might use something like:

url = Import["http://www.greatfallsmt.net/recreation/city-parks", 
   "Data"];
parks = url[[1, 2, 1, 1, 2]][[All, 1]];
images = {}; For[i = 1, i <= Length[parks], i++, 
 result = Import[
   StringJoin[
    "https://ajax.googleapis.com/ajax/services/search/images?v=1.0&q=",
    StringReplace[parks[[i]], " " -> "+"], 
    "+Montana+Great+Falls+Park+City"], "JSON"]; 
 AppendTo[images, 
  Import["url" /. ("results" /. ("responseData" /. result))[[1]]]]]

to get the photos from google. This does not work quite yet, but one could download more than one image per search and then choose the best one.

Best wishes from Aberdeen,

Marco

Hi,

I have just had another idea which is certainly not doable with WolframAlpha alone. I found this website, which lists city parks in Great Falls. We can import the website

url = Import["http://www.greatfallsmt.net/recreation/city-parks", "Data"];

and then extract a list of all parks.

parks = url[[1, 2, 1, 1, 2]][[All, 1]]

This gives a rather long list:

{"Anaconda Hills Golf Course", "BelView", "Bloomingdale", "Boston 
Heights", "Broadwater Bay", "Carter", "Charles Russell", "Chowen 
Springs", "Clara", "Community Hall", "Dudley Anderson", "Eagle Falls 
Golf Club", "Eagles Crossing", "Elks Riverside", "Fox Hollow", 
"Garden Home", "Gibson", "Grande Vista", "Graybill", "Heren", 
"Highland", "Horizon", "Hylande Heights", "Jaycee (Gallatin)", 
"Kiwanis - North", "Kiwanis - West", "Kranz", "Lion's", "Madison", 
"Margaret", "Meadowlark", "Memorial", "Mitchell Pool", "Montana", 
"Morony", "Multi Sports Complex", "Noah's Ark", "Oddfellow", 
"Overlook", "Pinski", "Rhodes", "Riverview", "Roosevelt", 
"Sacajawea", "Sandhills", "Sight & Sound", "Skyline", "Skyline 
Optimist", "Sunnyside", "Sunrise", "Tourist", "Valleyview", "Verde", 
"Vereran's Memorial", "Wadsworth", "Warden", "West Bank", "West 
Viaduct", "Westwood", "Whittier"}

In order to get the geo positions of these parks we use Google Maps. First we need to generate a query string; I'll show it for the first park:

StringJoin["http://maps.google.com/maps/api/geocode/json?address=", StringReplace[parks[[1]], " " -> "+"], "+Great+Falls", ",+Montana&sensor=false"]

This gives:

"http://maps.google.com/maps/api/geocode/json?address=Anaconda+Hills+Golf+Course+Great+Falls,+Montana&sensor=false"

We then need to extract the coordinates from the website. This would have been easy had I used:

Import["http://maps.google.com/maps/api/geocode/json?address=Anaconda+\Hills+Golf+Course,+Montana&sensor=false", "JSON"]

But when I first tried it I did not use the "JSON" option. I extracted the coordinates for all parks using:

coordsallparks = 
 DeleteDuplicates[
  Quiet[GeoPosition[{ToExpression@
        StringTake[
         StringSplit[
           StringSplit[StringSplit[#, "location"][[2]], "lat"][[2]], 
           ","][[1]], -10], 
       ToExpression@
        StringTake[
         StringSplit[
           StringSplit[StringSplit[#, "location"][[2]], "lat"][[2]], 
           ","][[2]], -27 ;; -15]}] & /@ (Import[#] & /@ (StringJoin[
          "http://maps.google.com/maps/api/geocode/json?address=", 
          StringReplace[#, " " -> "+"], "+Great+Falls", 
          ",+Montana&sensor=false"] & /@ parks))]]

instead. I then deleted the failed requests and one "outlier".

parkpos = Select[coordsallparks, (NumberQ[#[[1, 1]]] && NumberQ[#[[1, 2]]] && #[[1, 1]] < 50) &]

This gives:

{GeoPosition[{47.4942, -111.283}], GeoPosition[{47.4731, -111.341}], 
 GeoPosition[{47.5158, -111.34}], GeoPosition[{47.5059, -111.249}], 
 GeoPosition[{47.4955, -111.309}], GeoPosition[{47.7854, -111.334}], 
 GeoPosition[{47.5102, -111.286}], GeoPosition[{47.4981, -111.279}], 
 GeoPosition[{47.4951, -111.231}], GeoPosition[{47.4963, -111.248}], 
 GeoPosition[{47.4763, -111.324}], GeoPosition[{47.4653, -111.235}], 
 GeoPosition[{47.4735, -111.333}], GeoPosition[{47.5101, -111.23}], 
 GeoPosition[{47.4611, -111.256}], GeoPosition[{47.5325, -111.314}], 
 GeoPosition[{47.4865, -111.303}], GeoPosition[{47.5113, -111.267}], 
 GeoPosition[{47.5097, -111.325}], GeoPosition[{47.5014, -111.279}], 
 GeoPosition[{47.4955, -111.259}], GeoPosition[{47.5494, -111.499}], 
 GeoPosition[{47.582, -111.063}], GeoPosition[{47.4926, -111.307}], 
 GeoPosition[{47.492, -111.306}], GeoPosition[{47.4987, -111.226}], 
 GeoPosition[{47.5073, -111.326}], GeoPosition[{47.5304, -111.307}], 
 GeoPosition[{47.5483, -111.505}], GeoPosition[{47.5333, -111.295}], 
 GeoPosition[{47.4889, -111.267}], GeoPosition[{47.5341, -111.301}], 
 GeoPosition[{47.5373, -111.302}], GeoPosition[{47.4904, -111.282}], 
 GeoPosition[{47.502, -111.222}], GeoPosition[{47.5216, -111.333}], 
 GeoPosition[{47.4918, -111.305}], GeoPosition[{47.5129, -111.312}], 
 GeoPosition[{47.5065, -111.341}], GeoPosition[{47.5088, -111.293}]}

If we assume that these are the coordinates of the parks, we can find the order of park visits for our tour:

order = Last[
  FindShortestTour[
   GeoPosition /@ (Select[
      coordsallparks, (NumberQ[#[[1, 1]]] && 
         NumberQ[#[[1, 2]]] && #[[1, 1]] < 50) &])]]

Last but not least we can plot that:

GeoGraphics[GeoPath[parkpos[[order]][[All, 1]]]]

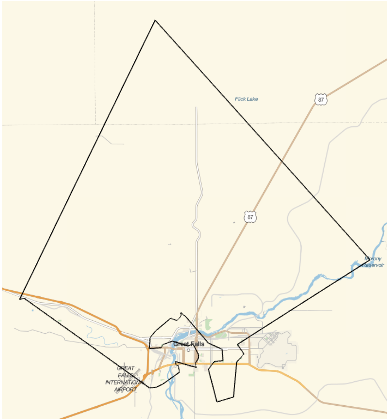
Hope this helps,

Marco

PS: Looking at the graphic I don't think that all of the parks qualify as city parks....

Dear Patrick,

I might be wrong, but I don't think that WolframAlpha will know the city parks in Great Falls. In fact, I would recommend to register for a free account on the Wolfram Cloud where you can get access to the full Wolfram language. If you type in

CommonName@EntityProperties[Entity["City", {"GreatFalls", "Montana", "UnitedStates"}]]

you obtain a long list of known data about Great Falls:

{"administrative region", "number of aggravated assaults", "rate of aggravated assault", "aggregate home value", "aggregate home value, householder 15 to 24 years", "aggregate home value, householder 25 to 34 years", "aggregate home value, householder 35 to 64 years", "aggregate home value, householder 65 years and over", "aggregate household income", "airport codes", "fuel spent in delays", "total fuel spent in delays", "average annual delay", "total annual delay", "area", "area code", "arterial street traffic", "arterial street length", "average public transit trip distance", "number of burglaries", "rate of burglary", "city sales tax", "country", "county", "county sales tax", "total rate of crime", "total number of crimes", "average daily traffic delay", "elevation", "number of rapes", "rate of rape", "freeway traffic", "freeway length", "Gini index", "FHFA home price index", "FHFA home price index annual average", "housing affordability index", "households", "number of larcenies", "rate of larceny", "latitude", "longitude", "total magnetic field strength", "median age", "median home sale price", "median home value", "median household income", "number of motor vehicle thefts", "rate of motor vehicle thefts", "incidents of murder and nonnegligent manslaughter", "rate of murder and nonnegligent manslaughter", "name", "next daylight saving shift", "nicknames", "number of owner-occupied housing units", "average daily peak period travelers", "peak period travelers per capita", "average daily peak period vehicles", "notable people born in city", "notable people who died in city", "per capita income", "polygon", "city population", "population by educational attainment", "population by migration in previous 12 months", "population by language spoken at home", "population by marital status", "population by poverty status", "population by school enrollment", "population density", "coordinates", "last daylight saving shift", "total rate of property crime", "total number of property crimes", "total public transit use", "unlinked public transit trips", "4 bedroom apartment fair market rent", "1 bedroom apartment fair market rent", "3 bedroom apartment fair market rent", "2 bedroom apartment fair market rent", "studio apartment fair market rent", "number of robberies", "rate of robbery", "daily rush hour length", "state sales tax", "time zone", "total daily traffic delay", "total sales tax rate", "average peak travel time", "unemployment rate", "unweighted sample housing units", "unweighted sample population", "total rate of violent crime", "total number of violent crimes", "ZIP codes"}

This is quite a wealth of information, but I cannot find anything about the city parks. I don't think that WolframAlpha will know them either. I will show you how to solve the problem in principle with the Wolfram Language for non-city parks in Montana. First we need the geo-coordinates of the parks in Montana.

coordinates = GeoPosition[#] & /@ (GeoEntities[Entity["AdministrativeDivision", {"Montana", "UnitedStates"}], "Park"]);

Then we can construct a graphic of the shortest tour:

GeoGraphics[{Red, Thick, Line@((coordinates[[Last[FindShortestTour[coordinates]]]]))}]

If you were to substitute the coordinates by coordinates for the city parks these functions should do the trick in the Wolfram Language.

I know that this does not solve your problem, because I do neither deal with city parks nor do I use WolframAlpha.

Best wishes,

M.